Д

А) б)

Рис. 2.38

оказательство.Доказательство обеих частей теоремы проведем одновременно.

Необходимость. Пусть в графеG существует эйлеров путь изав b. Тогда– нечетное число. Действительно, изавыходит по крайней мере одно ребро, обозначим егое₁. Если путь возвращается в а по ребруе₂, то он должен и выходить из него по ребруе₃, и так далее (рис. 2.38,а). Степень вершиныа– нечетная. Аналогично для вершиныb. Если путь изава– эйлеров цикл, то первое и последнее ребро цикла инцидентныа. Если вершинаавстречается внутри цикла, то вместе с ребромон содержит и ребро. Степень вершиныа – четная. Остальные вершины – внутренние и для эйлерова пути, и для эйлерова цикла, поэтому, если путь или цикл содержит ребро, то он содержит и ребро, если. Так как все ребра в пути и цикле встречаются ровно один раз, то степень вершины– четная (рис. 2.38,б).

Д

Рис. 2.39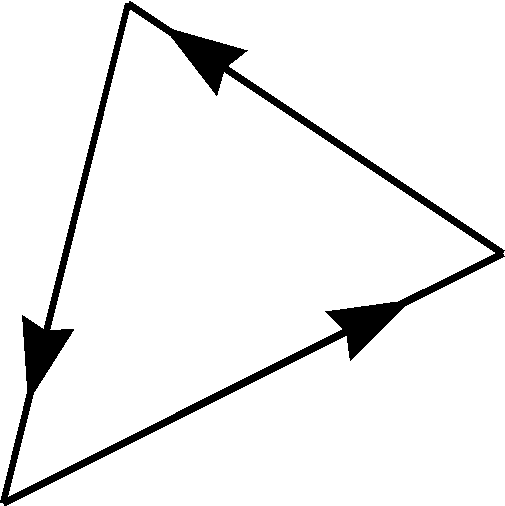

остаточность. Доказательство проведем индукцией по количеству ребер. Пусть,– нечетные. Наименьшее количество ребер равно 1. При этом графGсостоит из двух вершинаиbи соединяющего их ребра, который и будет являться эйлеровым путем. Если степени всех вершин четные, то наименьшее количество ребер равно трем (при отсутствии кратных ребер). Если степени всех вершин четные, возможен только граф, изображенный на рис. 2.39. Эйлеров цикл существует. Предположим, для графа с количеством ребер, меньшимп, утверждение истинно. Докажем утверждение для графа спребрами. Удалим произвольное ребро, выходящее иза. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершинуа. Если удалено ребро (а,b), то степени всех вершин нового графа четны, граф связный, и по индукционному предположению, в нем существует эйлеров цикл. Его можно начинать из произвольной вершины. Для нового графа рассмотрим эйлеров цикл изbвb. Присоединив к нему ребро (а,b) (возможно вместе с вершинойа), получим эйлеров путь изbва в исходном графе.

Если произвольное ребро, выходящее из а, – это ребро (а,с),, то, удалив его, получим, что степень вершиныастала четной, а степень вершиныс– нечетной, число ребер уменьшилось на 1. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершинуа. В новом графеG'также две вершины с четными степенями (bи с), остальные – с нечетными степенями. По предположению индукции вG'существует эйлеров путь изсв b. Добавив к нему ребро (а,с), получим эйлеров путь иза вb.

Докажем теперь утверждение для эйлерова цикла с пребрами. Пусть связный графGимеет вершины только с четными степенями. Удалив из него одно ребро, например, (а,b) , получим графG', у которого степени двух вершин нечетны, остальные – четны. Предположим, что удаление ребра нарушило связность графа, т.е. у графаG'две компоненты связностиG₁иG₂, при этом вершины с нечетными степенямиаиbнаходятся в разных компонентах связности. Тогда сумма степеней вершин для каждого из графовG₁иG₂нечетна, чего не может быть. Следовательно, графG'– связный, и по индукционному предположению в нем существует эйлеров путь изавb. Добавив к эйлерову пути ребро (а,b), получим эйлеров цикл. Теорема доказана.

Теорема о цикломатическом числе

Напомним, что цикломатическим числомграфаGназывается число, где– число ребер,– число вершин,– число компонент связности графаG. Было доказано, что для любого графа, для дерева.

Теорема. Если графсостоит из нескольких компонент связности, то.

Доказательство.Так как графы– связные графы, то, …,. Сложив почленно эти равенства, получим. Теорема доказана.

В

Рис. 2.40

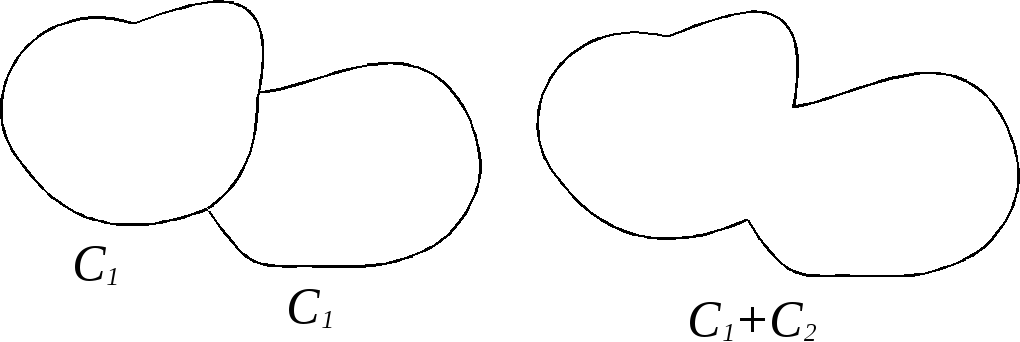
ведем определение суммы циклов произвольного графа. ПустьС₁иС₂ – произвольные циклы графаG, содержащие общие участки пути, соединяющие вершины и , и и так далее. Тогдасуммой циклов С₁иС₂ будем называть граф, вершинами которого являются все вершины цикловС₁иС₂, за исключением внутренних вершин их общих участков, а ребрами – все их ребра, за исключением ребер, составляющих их общие участки (рис. 2.40). Если циклыС₁иС₂не имеют общих участков, то ихсуммойназывается объединение цикловС₁ + С₂ = С₁  С₂. Вообще говоря, сумма двух циклов, даже и имеющих общие ребра, может не являться сама циклом, но является объединение простых циклов. Далее под циклом везде подразумевается либо простой цикл, либо объединение простых циклов. Очевидно, что,. По сложению циклы образуют абелеву группу.

Если граф Gимееттребере₁,е₁, …е_т, то любому циклуС графаGможно поставить в соответствие двоичный код длиныт:,

Если циклу С₁ соответствует код, а циклуС₂ – код, то циклуС₁+С₂соответствует код, где сложение производится по модулю 2. Таким образом, множество циклов графаGможно рассматривать, как подгруппу группы. Циклы образуют линейное пространство над полем.

Теорема. Пусть дан произвольный графG(без петель, без кратных ребер, с конечным числом вершин) и. Тогда:

1. Из графа Gможно удалитьkребер так, что оставшийся граф будет без циклов и будет иметь столько же компонент связности, что иG.

2. Размерность пространства циклов графа Gравнаk.

Доказательство. . Докажем, чтотогда только тогда, когда в графеGнет циклов. Действительно, если, а– компоненты связности графаG, то. Так как, топри всяком . Имеем, следовательно,– дерево, а значит, внет циклов. Таким образом, в графеGтоже нет циклов.

Докажем, что если в графе Gнет циклов, то. Действительно, тогдаG– лес,, где,– компоненты связности графаG, т.е. деревья. Так как для дерева, то.

Таким образом, мы доказали, что если для графа G , то в нем нет циклов.

Пусть теперь . Тогда вG есть циклы. Возьмем произвольно циклС₁,е₁– произвольное ребро этого цикла. Тогда графимеет то же количество компонент связности, что иG.. Если, то полученный граф будет без циклов. Если, то аналогично берем циклС₂и реброе₂и т.д. Этот процесс состоит ровно изшагов. На каждом шаге количество компонент связности не меняется. Графявляется лесом, количество компонент связности у него такое же, как и уG.

. Занумеруем остальные ребра графа G:. Тогда цикламС₁, …,С_kсоответствуют коды

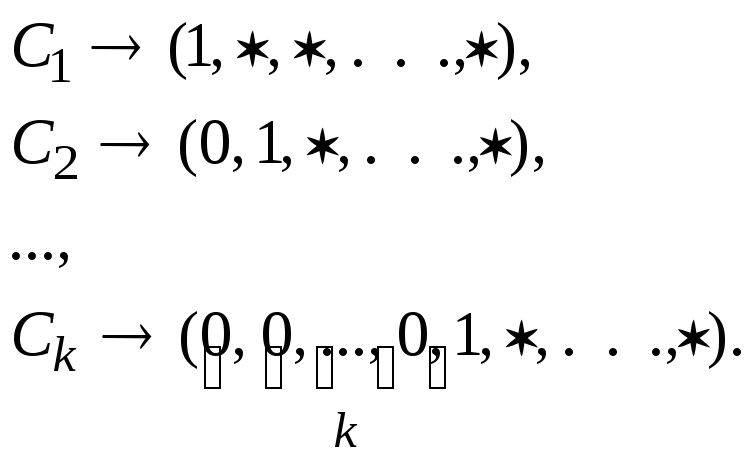
Строки кодов линейно независимы. Осталось доказать, что любой цикл графа Gможно линейно выразить через циклыС₁,С_2,…,С_k.. Возьмем произвольный циклСс соответствующим ему кодом. Строки

линейно независимы, следовательно, образуют базис в пространстве размерности k. Поэтому

при некоторых . Рассмотрим цикл

.

Учитывая, что , получаем

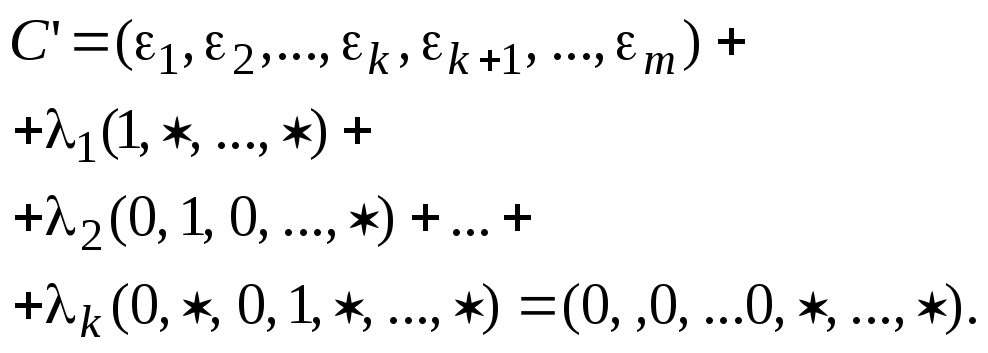
Таким образом, – цикл в графе. Но по построению,– граф без циклов. Следовательно,и, значит,

.

Теорема доказана.

Если G– связный граф и, то по только что доказанной теореме изGможно удалить некоторыеkребер так, чтобы получилось деревоТ. Назовем егоостовным деревом графа G. Аналогично, еслиG– несвязный граф, то изGможно удалить некоторыеkребер так, чтобы получился граф без циклов, т.е. лес, называемыйостовным лесом графа G.