2. Дискретная модель стержневой системы

Выбор дискретной расчетной модели стержневой системы начинается с разбиения расчетной схемы на элементы – на стержни постоянного сечения. В плоской стержневой системе эти элементы могут соединяться в шарнирном или жестком узлах (рис. 12.1):

шарнирный узел жесткий узел

Рис. 12.1

Здесь u₁, u₂, u₃ – независимые перемещения узла (u₁, u₂ – линейные перемещения, u₃ – угловое перемещение). У шарнирного узла число независимых перемещений равно двум, а у жесткого – трем. Они называются степенями свободы узла.

Общее число степеней свободы дискретной модели определяется суммой чисел степеней свободы отдельных узлов. Если обозначить его через n, а все перемещения узлов пронумеровать рядом натуральных чисел от 1 до n и объединить в единый вектор, получим

.

Он называется вектором перемещений дискретной модели.

Если в расчетной схеме имеются стержни переменного сечения, их следует представить в виде нескольких стержней постоянного сечения, а в места скачков сечений необходимо вводить узлы. В системах с криволинейными стержнями (в арках, кольцах и др.) криволинейные элементы следует заменять ломаной фигурой – многоугольником.

В дискретном методе нагрузка может быть приложена только в узлах. Однако в расчетной схеме нагрузка может быть и распределенной, и приложенной в виде сосредоточенных сил в точках, не совпадающих с узлами. Такие нагрузки следует переносить в соседние узлы как узловые силы, действующие в направлении степеней свободы дискретной модели. В результате этого формируется вектор внешней нагрузки

.

Внутренние усилия и деформации, которые требуется определить, также собираются в отдельные вектора

,

,

где S – вектор усилий, Δ – вектор деформаций, m – число усилий.

Внешнюю нагрузку в узлы можно переносить по-разному.

В качестве примера рассмотрим три варианта переноса распределенной нагрузки q, действующей на балку (рис. 12.2 а), в узел расчетной модели, введенной в середине этой балки (рис. 12.2 б).

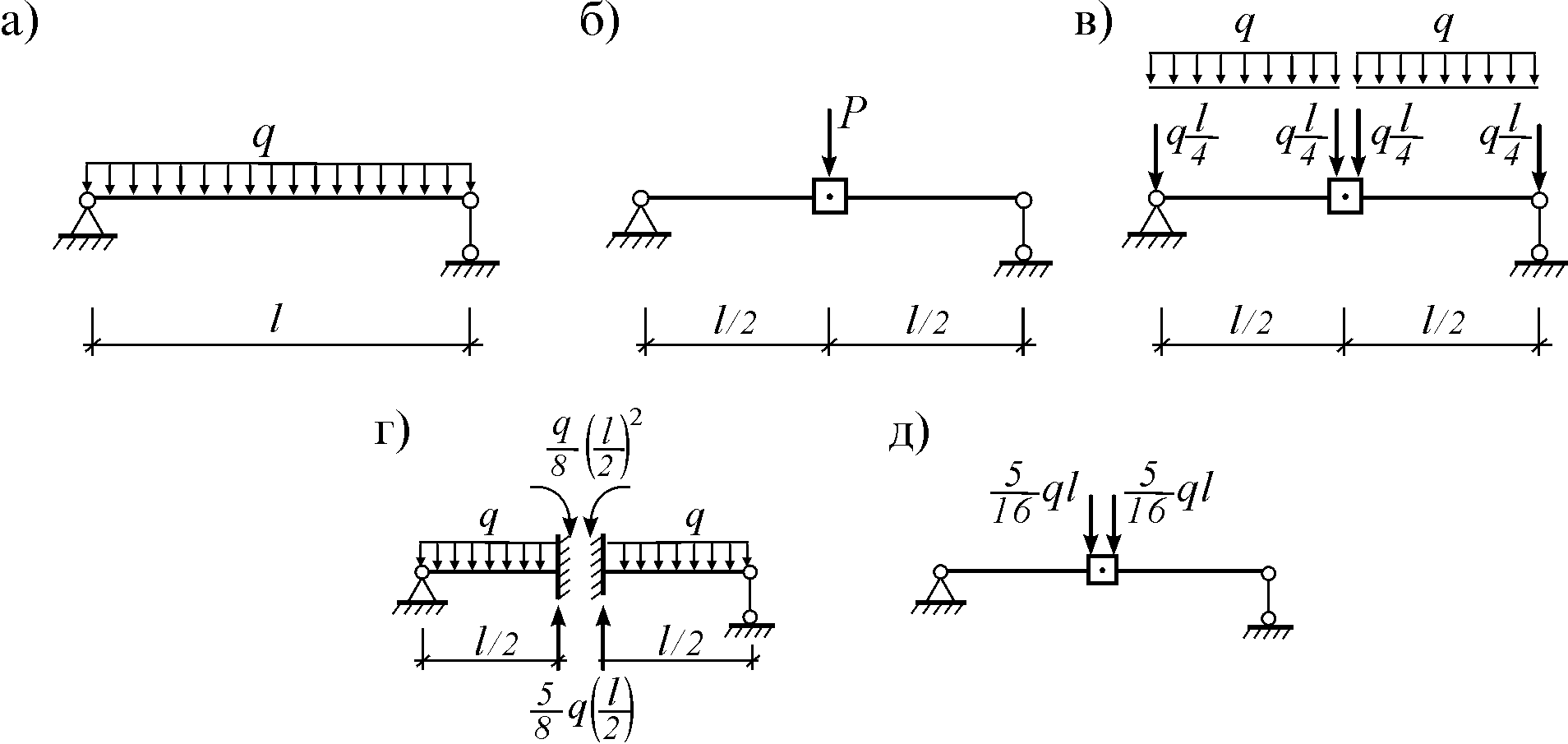
Рис. 12.2

а) Статически эквивалентный перенос

Поделим балку на два участка, а распределенную в них нагрузку учтем как давления ql/4 на концы участков балки (рис. 12.2 в). Давления на концы балки воспринимаются ее опорами, поэтому их можно не учитывать. Объединив оставшиеся две силы в середине балки, получим статически эквивалентную нагрузку, приложенную в середине балки:

.

б) Перенос с сохранением энергии

Решение этой задачи подробно рассматривать не будем. Отметим только, что для этого необходимо приравнять энергии рассматриваемой балки (рис. 12.2 а) и балки с сосредоточенной силой (рис. 12.2 б). В результате получается «точный» результат:

.

в) Перенос по таблице метода перемещений

Для этого следует исключить перемещения узла введением дополнительных связей и по таблице метода перемещений определить возникающие реакции во введенных связях (рис. 12.2 г). Если эти реакции сложить и приложить в обратном направлении (рис. 12.2 д), получим величину эквивалентной нагрузки:

.

Теперь сравним три варианта расчета. Конечно, вариант б) дает точный результат. Однако он сложен для реализации. Вариант а) наиболее прост, но дает неточный результат. Поэтому в дальнейшем будем пользоваться вариантом в), вполне простым для использования и дающим вполне точный результат.

В качестве примера рассмотрим следующую раму (рис. 12.3 а) и выберем ее расчетную модель (рис. 12.3 б). Для переноса нагрузок P и q в двух элементах рамы в узлы расчетной модели воспользуемся таблицей метода перемещений. Соответствующие схемы показаны на рис. 12.3 в, г. Полученные реакции с обратным знаком переносим в узлы выбранной расчетной модели (рис. 12.3 б).

Рис. 12.3