
- •Статистика предприятия
- •Часть I
- •1. Предмет и задачи статистики
- •1.2 Категории статистической науки
- •1.3 Задачи статистики
- •1.4 Организация статистики в Республике Беларусь
- •2.Статистическое наблюдение
- •2.1 Организационные формы наблюдения
- •2.2 Виды статистического наблюдения
- •2.3 Способы статистического наблюдения
- •2.4 Организация работы по статистическим наблюдениям
- •2.5 Ошибки статистического наблюдения
- •2.6 Контроль статистических данных
- •3 Сводка и группировка статистических материалов
- •3.1 Задачи сводки и ее основное содержание
- •3.2 Статистические группировки и их виды
- •3.2.1 Типологическая группировка
- •3.2.2 Структурная группировка
- •13.2.3 Аналитическая группировка
- •3.3 Вторичные группировки
- •3.4 Ряды распределения, их виды и графическое изображение
- •3.5 Статистические таблицы
- •3.6 Статистические графики
- •4 Обобщающие статистические показатели
- •4.1 Абсолютные величины, их виды, единицы измерения
- •4.2 Относительные величины, их виды и значения
- •4.3 Основные принципы построения относительных величин
- •4.4 Построение системы статистических показателей
- •5 Средние величины
- •5.1 Понятие средней величины. Виды средних величин
- •5.2 Средняя арифметическая, ее свойства и вычисление
- •5.3 Вычисление средней арифметической способом моментов
- •5.4 Средняя гармоническая, ее виды и вычисления
- •5.5 Мода и медиана. Их вычисление в дискретных и интервальных вариационных рядах
- •6 Показатели вариации
- •6.1 Характеристика показателей вариации
- •6.2 Показатели, характеризующие структуру и форму распределения признака
- •6.4 Дисперсия альтернативного признака
- •6.5 Определение тесноты связи между факторами. Правило сложения дисперсий
- •7 Индексы
- •7.1 Понятие об индексах. Их классификация. Индексная символика
- •7.2 Принципы и методы построения общих индексов
- •7.3 Построение индексов качественных показателей в агрегатной форме
- •7.4 Построение агрегатных индексов, объемных показателей
- •7.5 Построение агрегатного индекса производительности труда
- •7.6 Индексы с постоянными и переменными весами
- •7.7 Преобразование агрегатных индексов в индексы средние из индивидуальных
- •7.8 Индексный метод анализа факторов динамики (система взаимосвязанных индексов)
- •7.9 Индексы постоянного, переменного состава и влияния структурных сдвигов
- •7.10 Построение территориальных индексов
- •8 Статистическое изучение динамики
- •8.1 Ряды динамики и их виды
- •8.2 Темпы роста, их вычисление
- •8.3 Прирост и темп прироста. Абсолютное значение 1% прироста.
- •8.4 Вычисление средних показателей динамики
- •8.5 Приемы анализа рядов динамики
- •8.6 Аналитическое выравнивание ряда динамики
- •При четном числе уровней динамического ряда
- •8.7 Приемы анализа сезонных колебаний
- •9 Выборочное наблюдение
- •9.1 Общее понятие о выборочном методе и причины его использования
- •9.2 Способы отбора
- •9.2.1 Собственно случайная выборка
- •9.2.2 Механический отбор
- •9.2.3 Типический (районированный) отбор
- •9.2.4 Гнездовой (серийный) отбор
- •9.3 Понятие о моментном наблюдении и малой выборке
- •10 Статистическое изучение взаимосвязи
- •10.1 Виды связей
- •10.2 Измерение тесноты связи между атрибутивными признаками
- •10.2.1 Коэффициент взаимной сопряженности Чупрова и Пирсона
- •10.2.2 Коэффициенты ассоциации и контингенции
- •10.3 Измерение тесноты связи между количественными признаками
- •10.3. 1 Метод сравнения параллельных рядов
- •10.3.2 Коэффициент Фехнера
- •10.3.3 Коэффициент корреляции рангов
- •10.3.4 Метод аналитических группировок
- •10.4 Метод корреляционно-регрессионного анализа. Корреляционное отношение и коэффициент корреляции
- •10.5 Измерение тесноты связи между признаками
- •10.6 Проверка значимости корреляционной связи с помощью дисперсионного анализа
- •10.7 Понятие о многофакторном корреляционно-регрессионном анализе
- •Литература
- •Содержание
- •Статистика
- •212027, Могилев, пр-т Шмидта,3.
- •212027, Могилев, пр-т Шмидта,3.
8.2 Темпы роста, их вычисление
Темпы роста − это отношение уровней ряда одного периода к другому.
Темпы роста могут быть вычислены как базисные, когда все уровни ряда относятся к уровню одного и того же периода, принятому за базу:
Тр= yi/y0 − базисный темп роста
и как цепные,- это отношение каждого уровня ряда к уровню предыдущего периода:
Тр= yi/yi-1 − цепной темп роста.
Темпы роста могут быть выражены коэффициентом или процентом.
Базисные темпы роста характеризуют непрерывную линию развития, а цепные − интенсивность развития в каждом отдельном периоде, причём произведение цепных темпов равно темпу базисному. А частное от деления базисных темпов равно промежуточному цепному.
8.3 Прирост и темп прироста. Абсолютное значение 1% прироста.
Различают понятие абсолютного и относительного прироста. Абсолютный прирост вычисляют как разность уровней ряда и выражают в единицах измерения показателей ряда.
Если
из последующего уровня вычитается
предыдущий, то мы имеем цепной абсолютный
прирост:
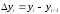
Если
из каждого уровня вычитается один и тот
же уровень − базисный, то это базисный
абсолютный прирост: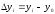
Между цепными и базисными абсолютными приростами существует следующая взаимосвязь: сумма последовательных цепных приростов равна соответствующему базисному приросту, характеризующему общий прирост за весь соответствующий период времени.
Относительную оценку значения абсолютного прироста по сравнению с первоначальным уровнем дают показатели темпа прироста (Т∆i). Его определяют двумя способами:
Как отношение абсолютного прироста (цепного) к предыдущему уровню:
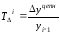
Это цепной темп прироста.
Как отношение базисного абсолютного прироста к базисному уровню:
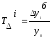
Это базисный темп прироста.
2 Как разницу между темпом роста и единицей, если темп роста выражен коэффициентом:
Т∆ = Тр-1, или
Т∆ = Тр- 100, если темп роста выражен в процентах.
Темп прироста показывает, на сколько процентов увеличились размеры явления за изучаемый период. Если темп прироста имеет знак минус, то говорят о темпах снижения.
Абсолютное значение 1-го процента прироста равно отношению абсолютного прироста (цепного) к цепному темпу прироста, выраженному в процентах:
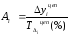 .
.
Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:
Аi = 0,01хУi;
8.4 Вычисление средних показателей динамики
Средний
уровень ряда
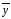 называется средней хронологической.
называется средней хронологической.
Средняя хронологическая − это средняя величина из показателей, изменяющихся во времени.
В интервальном ряду с равными интервалами средний уровень ряда определяется по формуле простой средней арифметической.
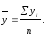
Средний уровень ряда в интервальном ряду динамики требует, чтобы было указано, за какой период времени он вычислен (среднемесячный, среднегодовой и т.д.).
Пример 1 Имеются следующие данные о товарообороте, ден.ед.:
|
Месяц |
январь |
февраль |
март |
|
Товарооборот |
200 |
195 |
220 |
Вычислить среднемесячный товарооборот за первый квартал.
Т.к. нам дан интервальный ряд с равными интервалами, применим формулу простой средней арифметической:
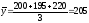
Если интервальный ряд имеет разные интервалы, то его вначале нужно привести к ряду с равными интервалами, а затем можно будет использовать формулу простой средней арифметической.
Пример 2 Имеются следующие данные о товарообороте, ден.ед.:
|
Месяц |
январь |
февраль |
март |
2-ой квартал |
|
Товарооборот |
200 |
200 |
200 |
600 |
Будем считать, что во втором квартале товарооборот распределялся по месяцам равномерно, тогда среднемесячный товарооборот за 1-ое полугодие:
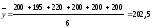
Так как показатели моментных рядов не обладают свойством суммарности, то среднюю нельзя вычислить, применяя формулу простой средней арифметической, в связи с тем, что остатки менялись непрерывно в течение месяца, а данные приводятся на определённый день.
Поэтому мы воспользуемся приближенным методом, основанным на предположении, что изучаемое явление менялось равномерно в течение каждого месяца. Чем короче будет интервал ряда, тем меньше ошибка будет допущена при использовании этого допущения.
Получим формулу :
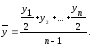
Эта формула применяется для вычисления среднего уровня в моментных рядах с равными интервалами.
Пример 3 Имеются данные об остатках строительных материалов на начало месяца, ден. ед.:
|
На дату |
1.01 |
1.02 |
1.03 |
1.04 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
Определить средний остаток за 1-й квартал.
Решение.
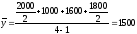 .
.
Если интервалы в моментных рядах не равны, то средний уровень ряда вычисляется по формуле:
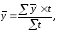
где
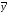 -
средний уровень в интервалах между
датами,
-
средний уровень в интервалах между
датами,
t - период времени (интервал ряда)
Пример 4Имеются данные об остатках сырья и материалов, ден. ед
|
На дату |
01.01 |
01.02 |
01.03 |
01.04 |
01.07 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
1760 |
Найти среднемесячные остатки сырья и материалов за первое полугодие.
Применяем формулу:
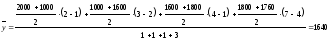
Средний абсолютный прирост вычисляется двумя способами:
1 Как средняя арифметическая простая годовых (цепных) приростов, т.е.
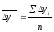 .
.
2 Как частное от деления базисного прироста к числу периодов:
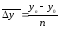 .
.
Расчет среднего абсолютного значения 1% приростаза несколько лет производится по формуле простой средней арифметической:

При вычислении среднегодового темпа роста нельзя применять простую среднюю арифметическую, т.к. сумма годовых темпов не будет иметь смысла. В этом случае применяют среднюю геометрическую, т.е.:

где Трi − годовые цепные темпы роста;
n − число темпов.
Поскольку произведение цепных темпов равно темпу базисному, то средний темп роста может быть рассчитан следующим образом:
Error: Reference source not found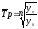
При расчёте по этой формуле не обязательно знать годовые темпы роста. Величина среднего темпа будет зависеть от соотношения начального и конечного уровня ряда.
Пример 5 Номинальная заработная плата работников народного хозяйства Республики Беларусь характеризуется данными, представленными в таблице 1.
Таблица 1 – Номинальная заработная плата работников народного хозяйства Республике Беларусь
|
Год |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
|
Размер заработной платы, тыс.р. |
558,9 |
1123,0 |
1189,2 |
2250,7 |
3347,5 |
4463,7 |
5582,2 |
7701,1 |
Для анализа динамики заработной платы определить:
среднегодовой размер заработной платы за 8 лет;
ежегодные и базисные абсолютные приросты, темпы роста и прироста заработной платы;
абсолютное значение 1% прироста;
среднегодовой абсолютный прирост;
среднегодовой темп роста и среднегодовой темп прироста;
среднее значение 1% прироста.
Результаты представить в таблице, сделать выводы.
Решение
1 Среднегодовой размер заработной платы определим по формуле средней арифметической простой
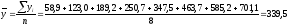 тыс.
р.
тыс.
р.
2
Ежегодный (цепной) абсолютный прирост
(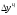 )
определим по формуле
)
определим по формуле
 ,
,
где
 ,
, – значение показателя соответственно
в
– значение показателя соответственно
в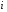 -м
периоде и предшествующем ему.
-м
периоде и предшествующем ему.
Например,
для 2005 года
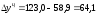 тыс. р., т. е. заработная плата в 2005 году
по сравнению с 2004 годом выросла на 64,1
тыс. р.; для 2006 года
тыс. р., т. е. заработная плата в 2005 году
по сравнению с 2004 годом выросла на 64,1
тыс. р.; для 2006 года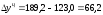 тыс. р. и т. д.
тыс. р. и т. д.
Базисный
абсолютный прирост (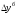 )
определим по формуле
)
определим по формуле
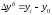 ,
,
где
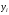 ,
,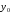 – значение показателя соответственно
в
– значение показателя соответственно
в -м
и базисном (2004 год) периоде.
-м
и базисном (2004 год) периоде.
Например,
для 2005 года
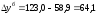 тыс. р.; для 2006 года
тыс. р.; для 2006 года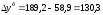 тыс. р., т. е. заработная плата в 2006 году
по сравнению с 2004 годом увеличилась на
130,3 тыс. р. и т. д.
тыс. р., т. е. заработная плата в 2006 году
по сравнению с 2004 годом увеличилась на
130,3 тыс. р. и т. д.
Цепной темп роста определим по формуле
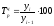 .
.
Например,
для 2005 года
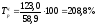 ,
т. е. заработная плата в 2001 году по
сравнению с 2004 годом выросла на 108,8%; для
2006 года
,
т. е. заработная плата в 2001 году по
сравнению с 2004 годом выросла на 108,8%; для
2006 года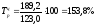 и т. д.
и т. д.
Базисный темп роста определим по формуле
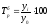 .
.
Например,
для 2001 года
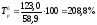 ;
для 2002 года
;
для 2002 года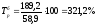 ,
т. е. заработная плата в 2002 году по
сравнению с
2000 годом выросла на 221,2% и т. д.
,
т. е. заработная плата в 2002 году по
сравнению с
2000 годом выросла на 221,2% и т. д.
Темп прироста найдем по формуле
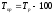 .
.
Так, цепной темп прироста
за
2005 год: 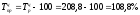 ;
;
за
2006 год: 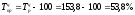 .
.
Базисный темп прироста
за
2005 год: 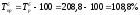 ;
;
за
2006 год: 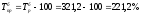 .
.
3
Абсолютное значение 1% прироста (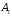 )
найдем по формуле
)
найдем по формуле
 .
.
Этот показатель можно также вычислить как одну сотую часть предыдущего уровня:
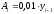 .
.
Например,
для 2005 года
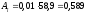 тыс. р.; для 2006 года
тыс. р.; для 2006 года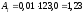 тыс. р.
тыс. р.
Расчеты показателей по пунктам 1, 2, 3 оформим в таблице 2
Таблица 2 – Показатели динамики заработной платы за 2004-2011 гг.
|
Год |
Размер заработной платы, тыс.р. |
Абсолютный прирост, тыс. р. |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста, тыс.р. | ||||||
|
Цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
| |||||
|
2004 |
58,9 |
- |
- |
- |
100 |
- |
- |
- | |||
|
2005 |
123,0 |
64,1 |
64,1 |
208,8 |
208,8 |
108,8 |
108,8 |
0,589 | |||
|
2006 |
189,2 |
66,2 |
130,3 |
153,8 |
321,2 |
53,8 |
221,2 |
1,23 | |||
|
2007 |
250,7 |
61,5 |
191,8 |
132,5 |
425,6 |
32,5 |
325,6 |
1,892 | |||
|
2008 |
347,5 |
96,8 |
288,6 |
138,6 |
590 |
38,6 |
490 |
2,507 | |||
|
2009 |
463,7 |
116,2 |
404,8 |
133,4 |
787,3 |
33,4 |
687,3 |
3,475 | |||
|
2010 |
582,2 |
118,5 |
523,3 |
125,6 |
988,5 |
25,6 |
888,5 |
4,637 | |||
|
2011 |
701,1 |
118,9 |
642,2 |
120,4 |
1190,3 |
20,4 |
1090,3 |
5,822 | |||
4 Среднегодовой абсолютный прирост вычисляется двумя способами:
– как средняя арифметическая простая годовых (цепных) приростов, т.е.:
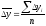 ;
;
– как частное от деления базисного прироста к числу периодов
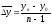 .
.
Так
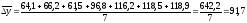 тыс.
р.
тыс.
р.
или
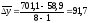 тыс. р.
тыс. р.
5 Среднегодовой темп роста найдем по формуле
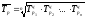 ,
,
где
 – число темпов роста цепных;
– число темпов роста цепных;
или
 ,
,
где
 – число периодов.
– число периодов.
Так
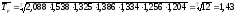 или 143%.
или 143%.
Либо
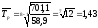 или 143%.
или 143%.
Среднегодовой темп роста заработной платы за 2004-2011 гг. составляет 143%, следовательно, среднегодовой прирост составит 43%.
6 Среднее значение 1% прироста рассчитаем по формуле
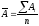 .
.
Так
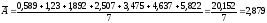 тыс. р.
тыс. р.
Таким образом, на протяжении 2004-2011 гг. наблюдается положительная динамика роста заработной платы. Так, среднегодовой абсолютный прирост составил 91,7 тыс. р. или 43%.
