5.5 Мода и медиана. Их вычисление в дискретных и интервальных вариационных рядах
Мода и медиана – особого рода средние, которые используются для изучения структуры вариационного ряда. Их иногда называют структурными средними, в отличие от рассмотренных ранее степенных средних.
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.
Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.
Медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.
Медиана показывает количественную границу значения варьирующего признака, которой достигла половина единиц совокупности. Применение медианы наряду со средней или вместо нее целесообразно при наличии в вариационном ряду открытых интервалов, т.к. для вычисления медианы не требуется условное установление границ отрытых интервалов, и поэтому отсутствие сведений о них не влияет на точность вычисления медианы.
Медиану применяют также тогда, когда показатели, которые нужно использовать в качестве весов, неизвестны. Медиану применяют вместо средней арифметической при статистических методах контроля качества продукции. Сумма абсолютных отклонений варианты от медианы меньше, чем от любого другого числа.
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:
|
Стаж, лет, X |
Число рабочих, чел, f |
Накопленные частоты |
|
1 |
2 |
2 |
|
3 |
4 |
6 |
|
4 |
5 |
(11) |
|
8 |
4 |
15 |
|
10 |
1 |
16 |
|
ИТОГО: |
16 |
- |
Определить моду и медиану.
Мода Мо = 4 года, так как этому значению соответствует наибольшая частота f = 5.
Т.е. наибольшее число рабочих имеют стаж 4 года.
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
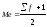
Ме=16/2=8
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.
Ме = 4 года.
Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Вычисление моды и медианы в интервальном вариационном ряду
Мода в интервальном вариационном ряду вычисляется по формуле
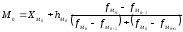
где ХМ0 - начальная граница модального интервала,
hм0 – величина модального интервала,
fм0, fм0-1, fм0+1 – частота соответственно модального интервала, предшествующего модальному и последующего.
Модальным называется такой интервал, которому соответствует наибольшая частота.
Пример 1
|
Группы по стажу |
Число рабочих, чел |
Накопленные частоты |
|
1 |
2 |
3 |
|
До 2 |
4 |
4 |
|
2-4 |
23 |
27 |
|
4-6 |
20 |
47 |
|
6-8 |
35 |
82 |
|
8-10 |
11 |
93 |
|
свыше 10 |
7 |
100 |
|
ИТОГО: |
100 |
- |
Определить моду и медиану.
Решение.
Модальный интервал [6-8], т.к. ему соответствует наибольшая частота f = 35. Тогда:
Хм0=6, fм0=35
hм0=2, fм0-1=20
fм0+1=11
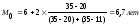
Вывод: Наибольшее число рабочих имеет стаж примерно 6,7 лет.
Для интервального ряда Ме вычисляется по следующей формуле:
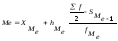
где Хме – нижняя граница медиального интервала,
hме – величина медиального интервала,
–
половина суммы частот,
fме – частота медианного интервала,
Sме-1 –сумма накопленных частот интервала, предшествующего медианному.
Медианный интервал – такой интервал, которому соответствует кумулятивная частота, равная или превышающая половину суммы частот.
Определим медиану для нашего примера.
Найдем:
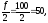
т.к 82>50, то медианный интервал [6-8].
Тогда:
Хме =6, fме =35,
hме =2, Sме-1=47,
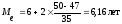
Вывод: Половина рабочих имеет стаж меньше 6,16 лет, а половина имеет стаж больше, чем 6,16 лет.