§8. Формулы Крамера.

Теорема 1.

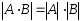
Теорема 2.

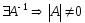
Присоединенная (взаимная, союзная) матрица – из алгебраических дополнений транспонированная:

a₁₁ ^. A₁₁+a₁₂ ^. A₁₂+ …+a_1n ^. A_1n = 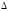, a₂₁ ^. A₁₁+ a₂₂ ^. A₁₂+ …+ a_2n ^. A_1n = = 0

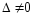Если , то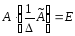, отсюда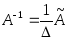- формула вычисленияА^1, подставляем в формулу из §5 Х=А^{1 .}В=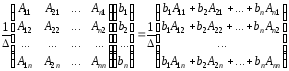

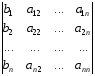=b₁A₁₁ +b₂A₂₁+… b_nA_n1=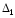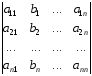=b₁A₁₂ +b₂A₂₂ +…+b_nA_n2 =

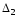
и т.д. – это числа из предыдущей матрицы.

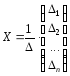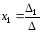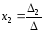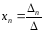
, то есть ,, …, это и есть формулы Крамера.

Глава 3. Функции. Пределы. Непрерывность.

§1. Множества. Логическая символика.

аА аА  АВ аА  аВ А = В, если АВ и ВА

1) А = а₁,а₂,…а_к  перечисление элементов 2) А = хТ(х) с помощью свойства (формулы)

АВ = ххА или хВ АВ = ххА и хВ А \ В = ххА, хВ

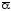
,  утверждения.  отрицание.   импликация.   эквивалентность.

  конъюнкция.   дизъюнкция. хХ х   квантор всеобщности

хХ х   квантор существования хХ х

§2. Функции вещественной переменной.

D  R x  D f ( x ) E = yRy = f ( x ), x  D f : D  E y = f ( x )

f : D  E x₁,x₂D x₁  x₂  f ( x₁ )  f ( x₂ ) yE xD : f ( x ) = y

f^-1 : E  D x = f^-1 ( y ) обратная функция

f : X  Y, g : Y  Z. Композиция ( сложная функция) h = g _ f : X  Z h ( x ) = g ( f ( x ))

Элементарные функции. 1. y = x^a, a R. 2. y = a^x, a > 0, a  1. 3. y = log_ax, a > 0, a  1.

4. y = sin x, y = cos x, y = tg x, y = ctg x. 5. y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

    x, y )  R²  x  D, y = f ( x ) 

§3. Предел последовательности вещественных чисел.

Последовательность f : N  R f ( n ) = x_n– n-й член последовательности  x_n  _nN

Число а называется пределом последовательности  x_n _nN ( 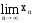=a ), если

>0 N: n> N x_n  a <  Сходящаяся последовательность

Геом. смысл. Вне интервала ( а  , а +  ) может находиться лишь конечное число x_n

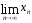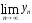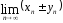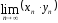Свойства. Если = a, = b, то 1. = a  b 2. = a^.b

§3. Предел последовательности вещественных чисел.

Последовательность: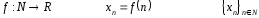

Число а называется пределом последовательности 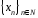, то есть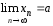, если

: .

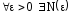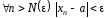Сходящаяся последовательность.

Геометрический смысл:

Вне интервала 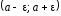может находиться лишь конечное число членов последовательности.

Свойства:

Если 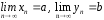, то

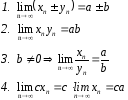
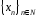- бесконечно малая, если .

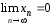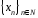- бесконечно большая, если

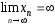
Число 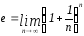- основание натурального логарифма.

Теорема 1 ( о сжатой последовательности).

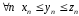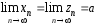Если и, то.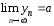

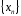называется ограниченной, если

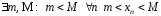
Теорема 2.

Если 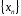- ограничена и не убывает (т.е.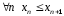), то.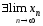

Следствие:

Если 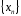- ограничена и не возрастает (т.е.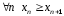), то.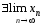

Теорема 3.

Если 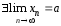, то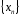- ограничена.

§4. Предел функции.

Пусть функция 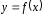определена на множествеD. Число а называется пределом функции 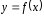в точкеx₀ (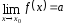), если

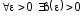такое, что .

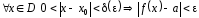«Замечательные» пределы:

1.

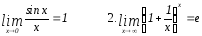
Свойства:

Если 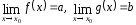, то