§ 1. Определение показательного распределения

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х₁ которое описывается плотностью

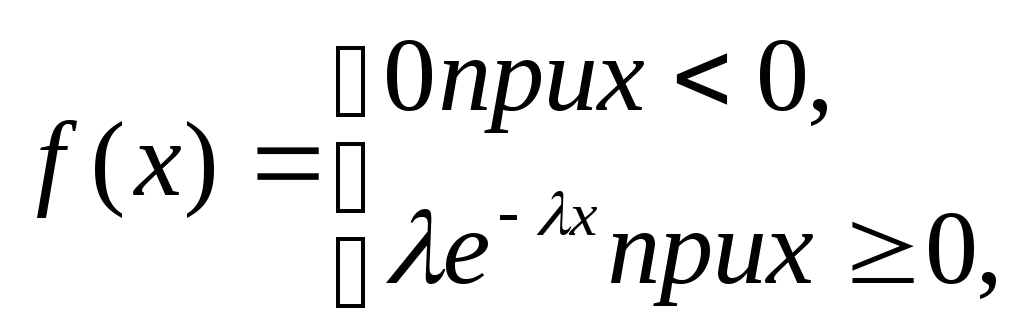
где  — постоянная положительная величина.

Мы видим, что показательное распределение определяется одним параметром . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большею числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т. д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (см. § 5).

Найдем функцию распределения показательного закона (см. гл. XI, § 3):

Итак,

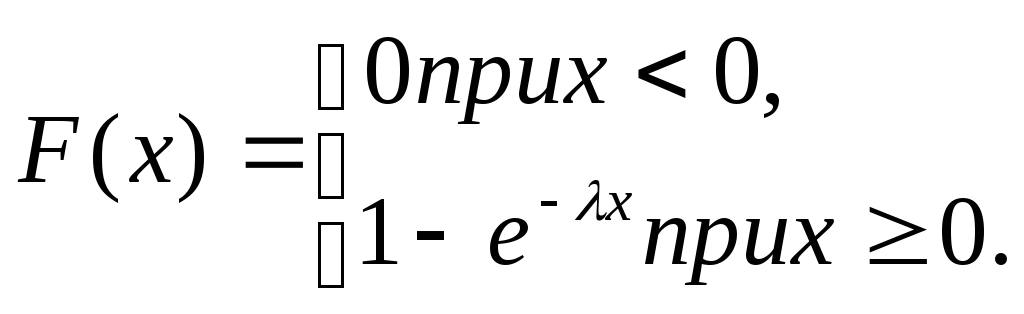
Мы определили показательный закон с помощью плотности распределения; ясно, что его можно определить, используя функцию распределения.

Графики плотности и функции распределения показательного закона изображены на рис. 12.

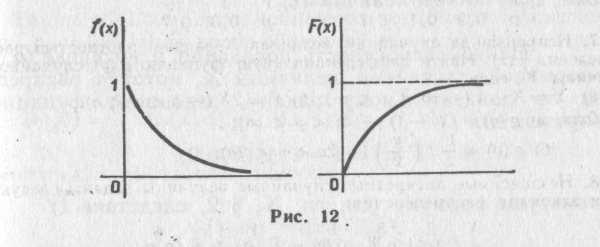
Пример. Написать плотность и функцию распределения показательного закона, если параметр  = 8.

Решение. Очевидно, искомая плотность распределения

f(х) = 8е^-8x при х0; f(x)=O при х < 0.

Искомая функция распределения

F(x) =1—e^-8x при x0; F(x) = 0 при х < 0.

§ 2. Вероятность попадания в заданный интервал показательно распределенной случайной величины

Найдем вероятность попадания в интервал (а,b) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения

Используем формулу (см. гл. X, § 2, следствие 1)

P(a<X<b) = F(b) — F(a).

Учитывая, что F(а)=,F(b)=,получим

P(a<X<b) =(*)

Значения функции е^-x находят по таблице.

Пример. Непрерывная случайная величина X распределена по показательному закону

f(x)=2e^-2x при х 0; f(x)=0 при х < 0.

Найти вероятность того, что в результате испытания X попадает в интервал (0,3, 1).

Решение. По условию,  = 2. Воспользуемся формулой (*):

Р (0,3 < X < 1)=е^-(2*0,3)-е^-(2*1)=е^-0,6-е^-2 = 0,54881—0,135340,41.

§ 3. Числовые характеристики показательного распределения

Пусть непрерывная случайная величина X распределена по показательному закону

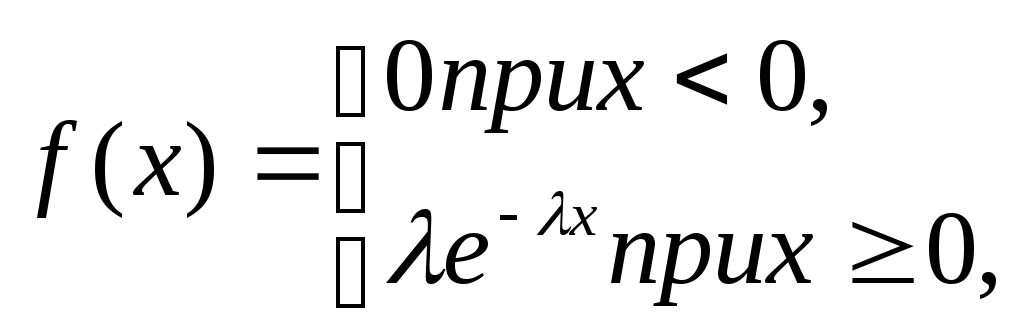
Найдем математическое ожидание (см. гл. XII, § 1):

Интегрируя по частям, получим

(*)

Таким образом, математическое ожидание показательного распределения равно обратной величине параметра ..

Найдем дисперсию (см. гл. XII, § 1):

Интегрируя по частям, получим

Следовательно,

D(X)=1/^

Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:

(X)=1/ (**)

Сравнивая (*) и (**), заключаем, что

М (Х) =(X)=1/

т. е. математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Пример. Непрерывная случайная величина X распределена по показательному закону

f(x)=5e^-5x при x0; f(x)=0 при x<0.

Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Решение. По условию,  = 5. Следовательно,

М (X) =  (X) = 1 / = 1 /5 = 0,2;

D(X)=1/^^

Замечание 1. Пусть на практике изучается показательно распределенная случайная величина, причем параметр  неизвестен. Если математическое ожидание также неизвестно, то находят его оценку (приближенное значение), в качестве которой принимают выборочную среднюю (см. гл. XVI, § 5). Тогда приближенное значение параметра находят с помощью равенства

^.

Замечание 2. Допустим, имеются основания предположить, что изучаемая на практике случайная величина имеет показательное распределение. Для того чтобы проверить эту гипотезу, находят оценки математического ожидания и среднего квадратического отклонения, т. е. находят выборочную среднюю и выборочное среднее квадратическое отклонение (см. гл. XVI, § 5, 9). Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, поэтому их оценки должны различаться незначительно. Если оценки окажутся близкими одна к другой, то данные наблюдений подтверждают гипотезу о показательном распределении изучаемой величины; если же оценки различаются существенно, то гипотезу следует отвергнуть.

Показательное распределение широко применяется в приложениях, в частности в теории надежности, одним из основных понятий которой является функция надежности.