§ 1. Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

Пусть непрерывная случайная величина X задана плотностью распределения f(x). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на п частичных отрезков длиной ,,..., и выберем в каждом из них произвольную точку x_i (i = 1, 2, ..., п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x_i на вероятности попадания их в интервал ; (напомним, что произведениеf(х) приближенно равно вероятности попадания X в интервал ):

Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

M(X)= (*)

Если возможные значения принадлежат всей оси Ох, то

M(X)=

Предполагается, что несобственный интеграл сходится абсолютно, т. е. существует интеграл Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к —, а верхнего—к +.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку[a,b], то

D(X)=

если возможные значения принадлежат всей оси х, то

D(X)=

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

(X)=.

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

D(X)= (**)

D(X)=

Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения

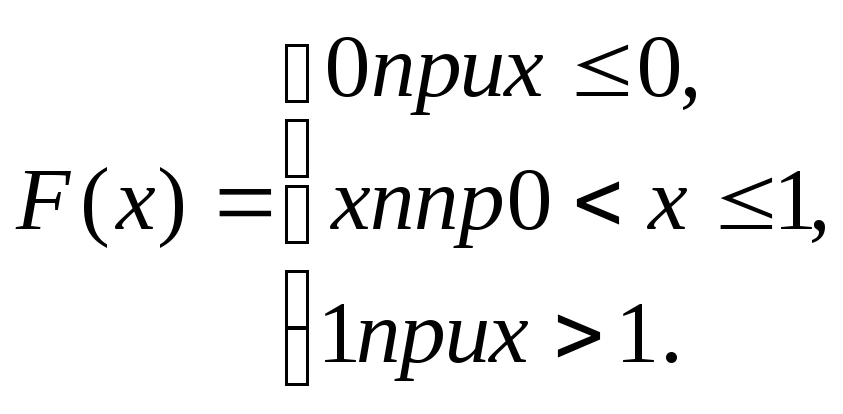
Решение. Найдем плотность распределения:

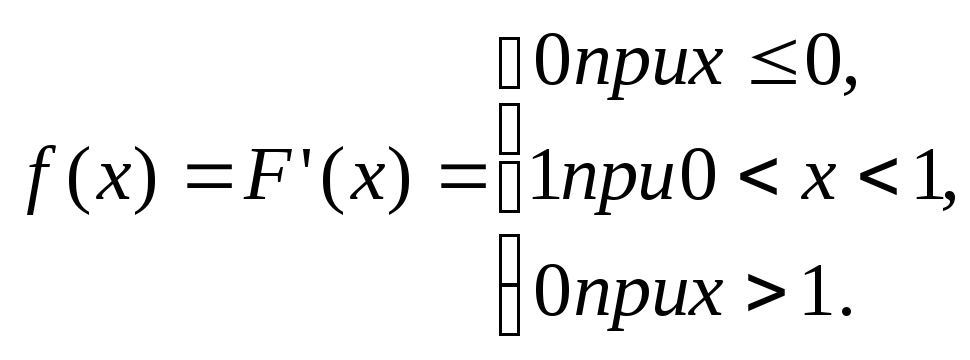
Найдем математическое ожидание по формуле (*):

M(X)=

Найдем дисперсию по формуле (**):

D(X)=

Пример 2. Найти математическое ожидание и дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, b).

Решение. Найдем математическое ожидание X по формуле (*), учитывая, что плотность равномерного распределения f (x) = 1/(b — а)(см. гл. XI, § 6):

M(X)=

Выполнив элементарные выкладки, получим

M(X)=(a+b)/2

Найдем дисперсию X по формуле (**):

D(X)=

Выполнив элементарные выкладки, получим

D(X) = (b — a)²/12.

Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т. е. если a = 0, b=1, как следует из примера 2, соответственно равны М (R) = 1/2, D(R)=l/12. Этот же результат мы получили в примере 1 по заданной функции распределения случайной величины R.

§ 2. Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Мы видим, что нормальное распределение определяется двумя параметрами: а и . Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, —среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины,

M(X)=

Введем новую переменную z = (x—а)/. Отсюда x=z+a, dx=dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

M(X)=

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно a ( интеграл Пуассона ).

Итак, М(Х) = а, т. е. математическое ожидание нормального распределения равно параметру а.

б) По определению дисперсии непрерывной случайной величины, учитывая, что М(Х) = а, имеем

D(X)=

Введем новую переменную z = (x—а)/. Отсюда х—a = z, dx = dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

D(X)=

Интегрируя по частям, положив u = z, dv=, найдем

D(X)=^

Следовательно,

(X)=.

Итак, среднее квадратическое отклонение нормального распределения равно параметру .

Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и  ( > 0).

Нормированным называют нормальное распределение с параметрами а = 0 и =1. Например, если X — нормальная величина с параметрами а и , то U =(X — а)/ — нормированная нормальная величина, причем M(U)=0, (U)=1.

Плотность нормированного распределения

Эта функция табулирована (см. приложение 1).

Замечание 2. Функция F(х) общего нормального распределения (см. гл. XI, § 3)

а функция нормированного распределения

Функция F_o (x) табулирована. Легко проверить, что

F(x)=F₀((x-a)/ ).

Замечание 3. Вероятность попадания нормированной нормальной величины X в интервал (0, х) можно найти, пользуясь функцией Лапласа Действительно (см.гл.XI, § 2),

P(0<X<x)=

Замечание 4. Учитывая, что (см. гл.XI, §4,свойство 2), и, следовательно, в силу симметрии (х) относительно нуля

, а значит, и Р (-< X < 0)=0,5,

легко получить, что

F₀(x)=0,5+(x).

Действительно,

F₀(x)=P(-<X<x)=P(-<X<0)+P(0<X<x)=0,5+(x).