§ 3. Теорема Чебышева

Теорема Чебышева. Если Х₁, Х₂,…, Х_n, ...—попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число е, вероятность неравенства

будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы

Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Доказательство. Введем в рассмотрение новую случайную величину — среднее арифметическое случайных величин

=(X₁+X₂+…+X_n)/n.

Найдем математическое ожидание . Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим

M=. (*)

Применяя к величине неравенство Чебышева, имеем

или, учитывая соотношение (*),

(**)

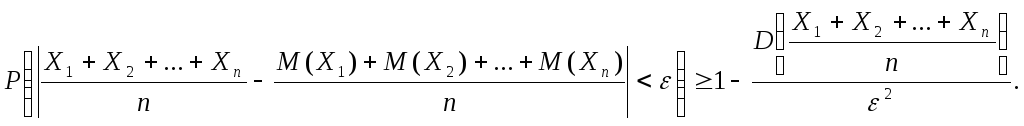Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим

.

По условию дисперсии всех случайных величин ограничены постоянным числом С, т. е. имеют место неравенства: D (X₁) C; D (X₂) C; ...; D (X_n) C, поэтому

(D (X₁)+ D (X₂) +…+D (X_n))/n² (C+C+…+C)/n²=nC/n²=C/n.

Итак,

. (***)

Подставляя правую часть (***) в неравенство (**) (отчего последнее может быть лишь усилено), имеем

Отсюда, переходя к пределу при , получим

Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать

Теорема доказана.

Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.

Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая.

Если Х₁, Х₂, ..., Х_п ,... —попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число  > О, вероятность неравенства

будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы будет иметь место равенство

§ 4. Сущность теоремы Чебышева

Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу (М (X₁) + М(Х₂) +...+М (Х_п))/п (или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.

Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.