Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Дипломная работа (подготовка и защита)

Файл:

IVAN / DIPLOM.DOC

Скачиваний:

Добавлен:

16.04.2013

Размер:

1.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 166 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Расчет передач редуктора

Берем унифицированный редуктор и проверяем его передачи на контактную прочность и напряжения изгиба в соответствии с нашими нагрузками.

Редуктор состоит из 4-х цилиндрических прямозубых передач.

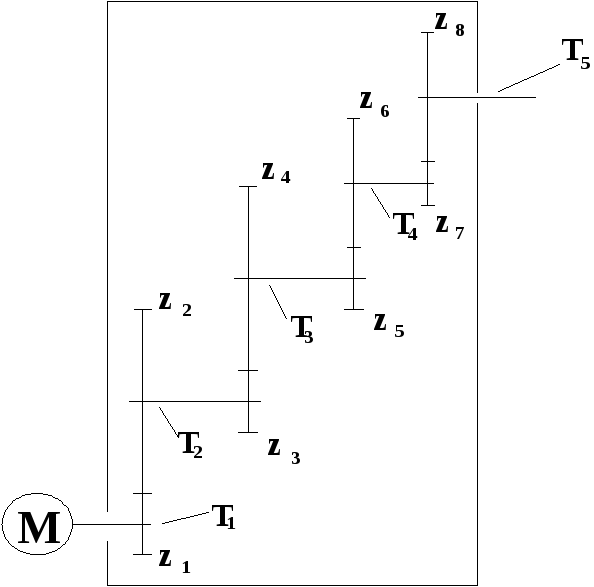
Основные параметры передач редуктора

Число зубьев

Модуль передачи

Передаточное число Межосевое расстояние

=51

=0.4

=5.67

=12 мм

=18

=48

=0.4

=2.67

=13.2 мм

=18

=45

=0.4

=2.5

=12.6 мм

=17

=35

=0.5

=2.05

=13мм

Считаем для передачи

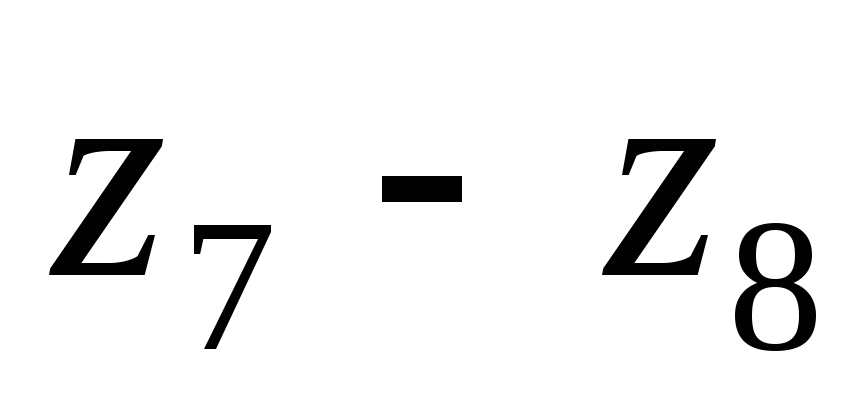
Параметры передачи необходимые для расчета:

Число зубьев: шестерни -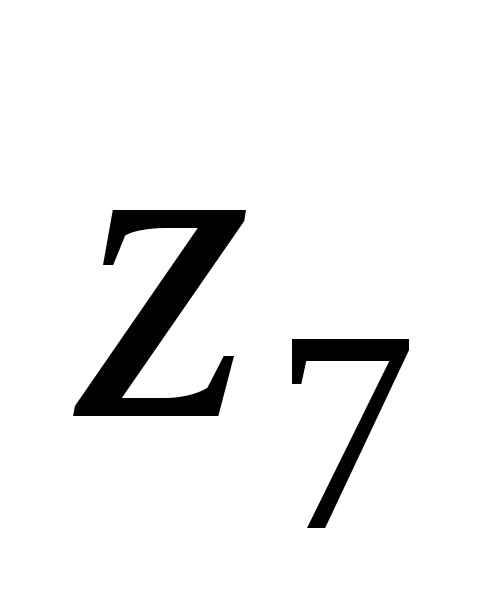=17, колеса -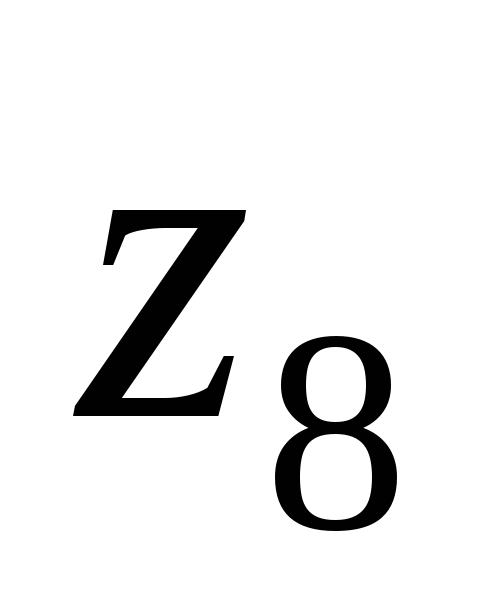=35.
Передаточное число =2.05.
Межосевое расстояние =13 мм.
Модуль передачи 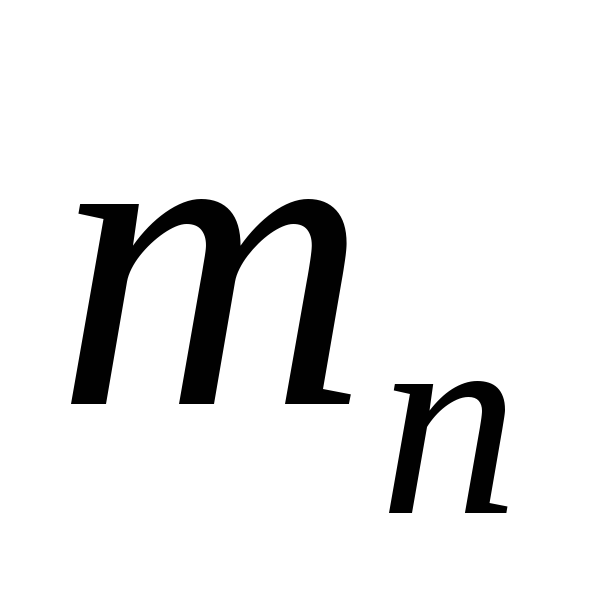=0.5.
Момент на ведомом колесе:

H м

Где - КПД 1-й пары подшипников качения,

- передаточное число открытой цилиндрической передачи,

- КПДоткрытой цилиндрической передачи

материалы зубчатых колес:

шестерни – сталь 40X (улучшение), твердостью HB=270,

колеса – сталь 40X (улучшение), твердостью HB=260.

Допускаемые контактные напряжения 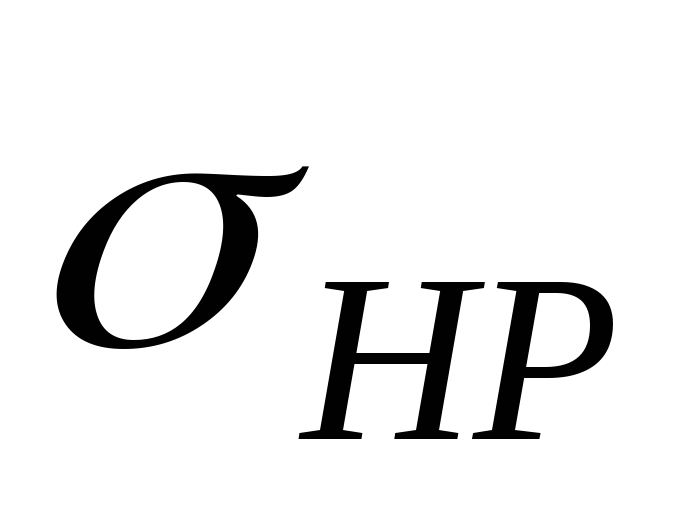для шестерни и колеса по формуле(7.7) и табл. 7.3.

для шестерни:

MПа,

MПа;

где - базовый предел контактной выносливости;

- коэффициент безопасности, для равномерной структуры (улучшение) =1.1.

для колеса:

MПа,

MПа;

В качестве расчетного допускаемого напряжения принимаем меньшее из двух, т.е. - =536 Mпа.

Допускаемые напряжения изгиба по формуле (7.3) и табл.7.4:

для шестерни: Mпа;

=260+ HB= 260+270=530 МПа;

для колеса: Mпа;

=260+ HB= 260+260=520 МПа;

где - базовый предел выносливости зубьев по излому(в зависимости от материала и термообработки);

- коэффициент безопасности;

- коэффициент, учитывающий влияние реверсивности приложения нагрузки;

Определяем диаметры делительных окружностей:

шестерни: 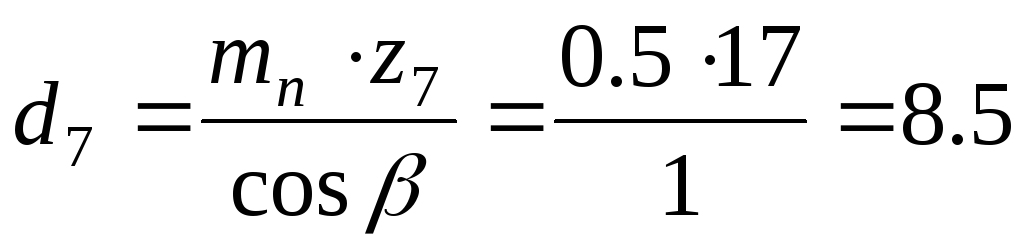мм
колеса: 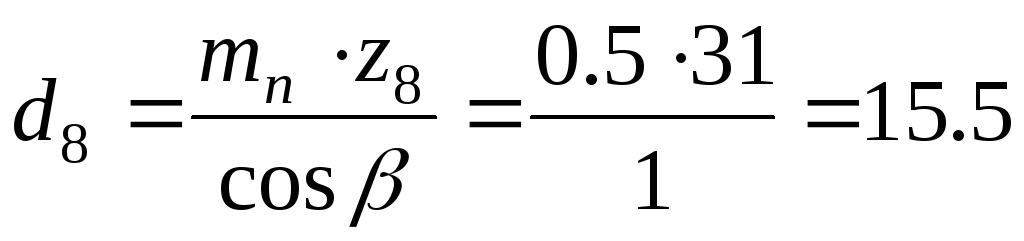мм.

Окружное усилие в зацеплении:

Считаем 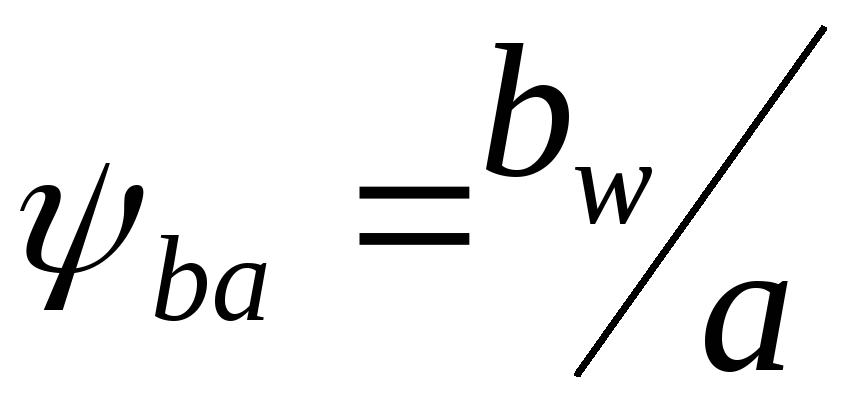-коэффициент ширины зубчатого венца колеса относительно межосевого расстояния. По табл. 1.8 определяем 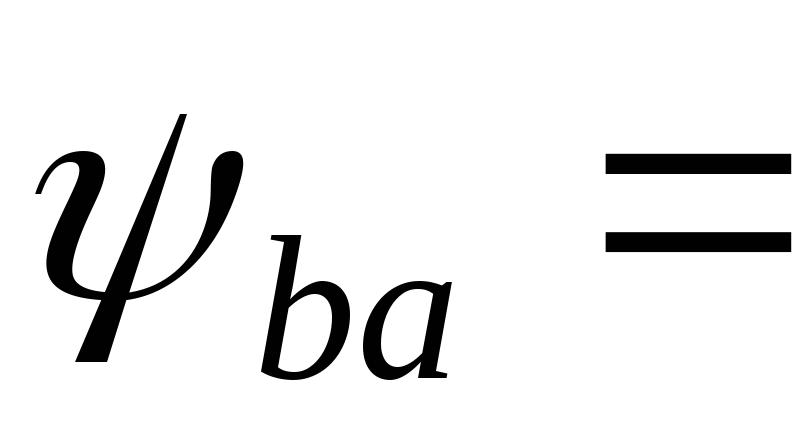0.25и определяем расчетную ширину колес:

мм

по принимаем 4 мм.

Фактическое контактное напряжение:

МПа

Здесь - коэффициент, зависящий от формы сопряженных поверхностей зубьев; для передач, составленных из нулевых колес ;

- коэффициент, учитывающий механические свойства материалов сопряженных колес; для стальных колес =275 МПа;

- коэффициент, учитывающий суммарную длину контактных линий; для прямозубых передач =1.

- коэффициент расчетной нагрузки;

- коэффициент концентрации нагрузки по ширине зубчатого венца, -коэффициент динамичности нагрузки; определяются из табл.1.6, табл.1.7 и формулы (1.6)

- коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых передач =1.

Таким образом МПа

Выполним проверочный расчет зубьев по напряжениям изгиба. По табл.1.10 в зависимости от

определяем

Вычисляем отношения

; ;

Расчет ведем по материалу шестерни, т.к.

Считаем:

МПа;

где - коэффициент формы зуба;

- коэффициент, учитывающий перекрытие зубьев, для прямозубых передач =1;

- коэффициент, зависящий от угла наклона зубьев,

;

- коэффициент расчетной нагрузки;

- коэффициент концентрации нагрузки по ширине зубчатого венца, -коэффициент динамичности нагрузки; определяются табл.1.6, табл.1.7 и формулой (1.6).

- коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых передач =1.

Таким образом

=218.23 МПа.

КПД цилиндрической передачи:

или 86%

где - поправочный коэффициент, учитывающий влияние нагрузки на КПД;

- коэффициент перекрытия, =1.5;

- коэффициент трения, =0.6.

Считаем для передачи

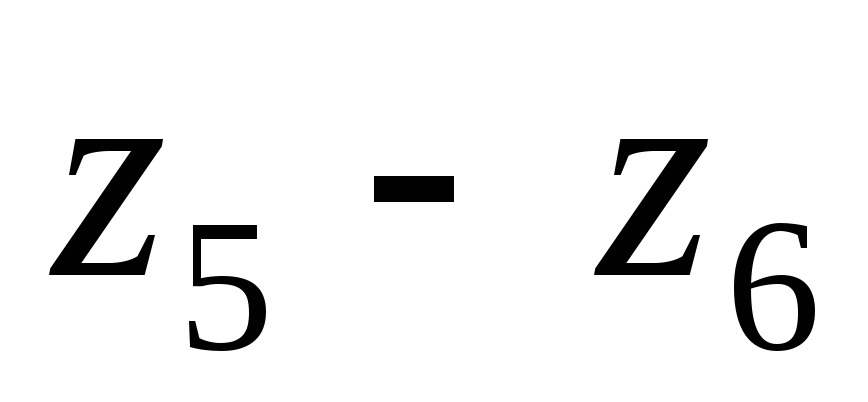
Параметры передачи необходимые для расчета:

Число зубьев: шестерни -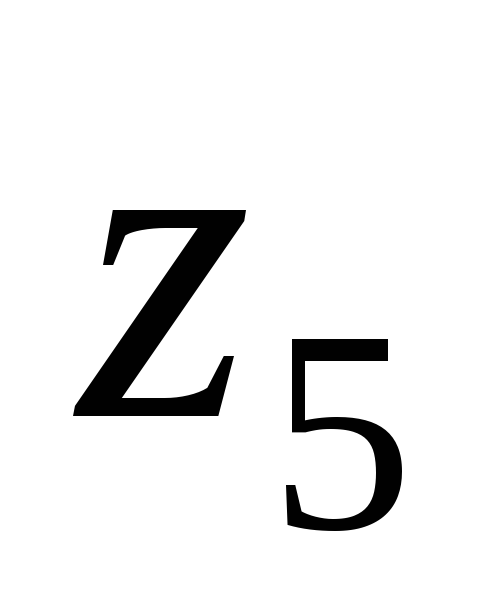=18, колеса -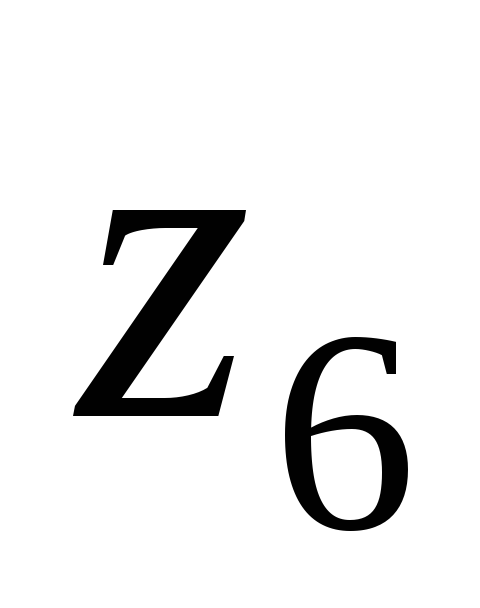=45.
Передаточное число =2.5.
Межосевое расстояние =12.6 мм.
Модуль передачи 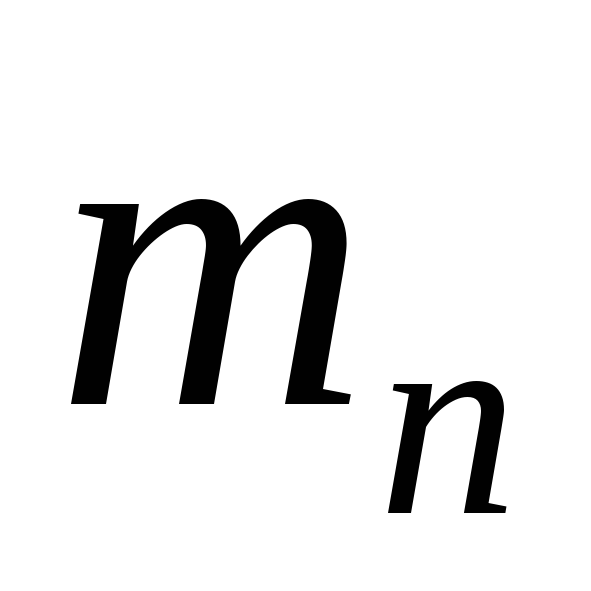=0.4.
Момент на ведомом колесе:

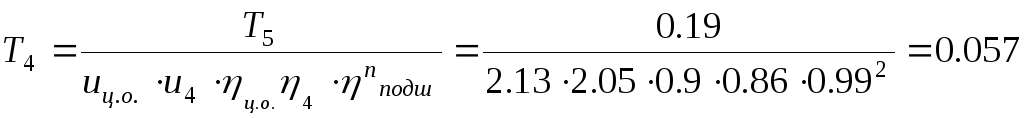H м

Где - КПД 1-й пары подшипников качения,

- число пар подшипников,

- передаточное число открытой цилиндрической передачи,

- КПД открытой цилиндрической передачи.

материалы зубчатых колес:

шестерни – сталь 40X (улучшение), твердостью HB=270,

колеса – сталь 40X (улучшение), твердостью HB=260.

Допускаемые контактные напряжения 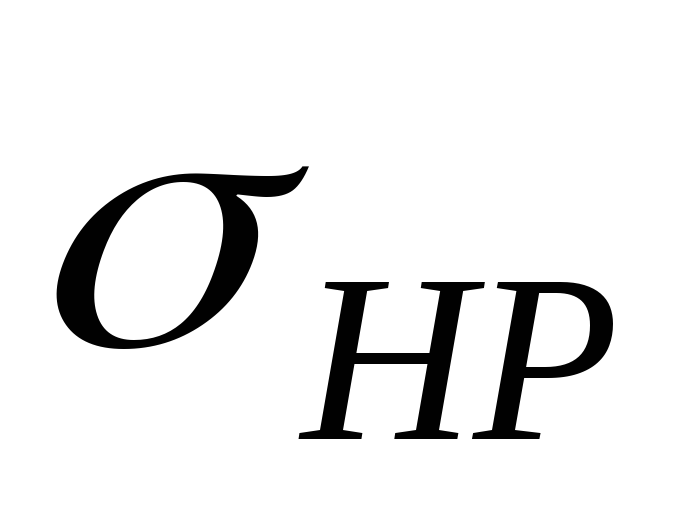для шестерни и колеса по формуле(7.7) и табл. 7.3.

для шестерни:

MПа,

MПа;

где - базовый предел контактной выносливости;

- коэффициент безопасности, для равномерной структуры (улучшение) =1.1.

для колеса:

MПа,

MПа;

В качестве расчетного допускаемого напряжения принимаем меньшее из двух, т.е. - =536 MПа.

Допускаемые напряжения изгиба по формуле (7.3) и табл.7.4:

для шестерни: MПа;

=260+ HB= 260+270=530 МПа;

для колеса: MПа;

=260+ HB= 260+260=520 МПа;

где - базовый предел выносливости зубьев по излому(в зависимости от материала и термообработки);

- коэффициент безопасности;

- коэффициент, учитывающий влияние реверсивности приложения нагрузки;

Определяем диаметры делительных окружностей:

шестерни: 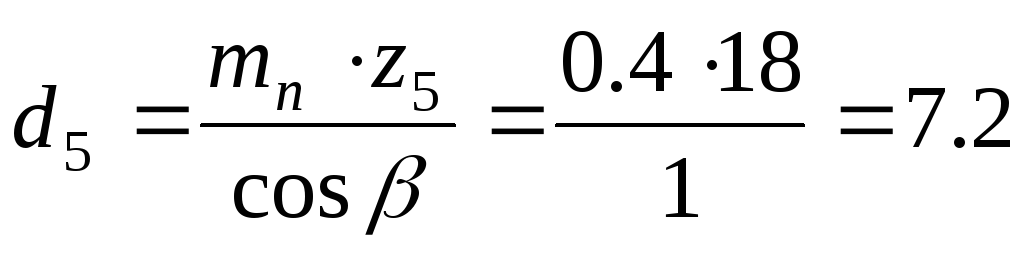мм
колеса: 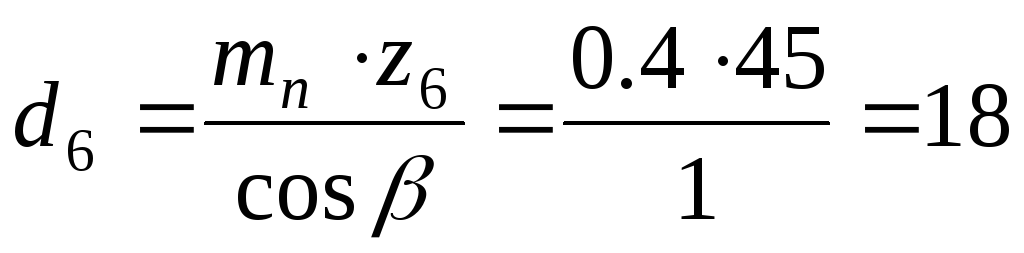мм.

Окружное усилие в зацеплении:

Считаем 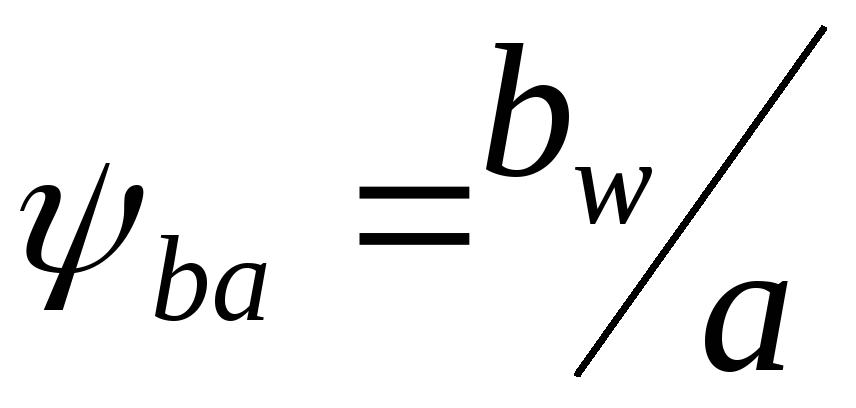-коэффициент ширины зубчатого венца колеса относительно межосевого расстояния. По табл. 1.8 определяем 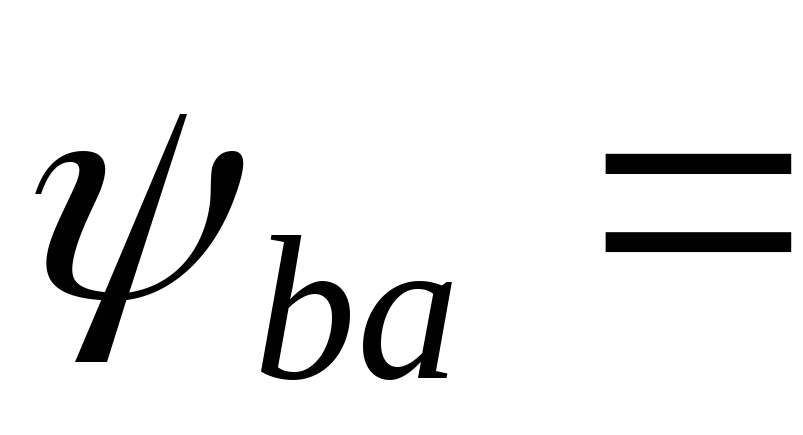0.3и определяем расчетную ширину колес:

мм

по принимаем 4 мм.

Фактическое контактное напряжение:

МПа

- коэффициент, учитывающий механические свойства материалов сопряженных колес; для стальных колес =275 МПа;

- коэффициент, учитывающий суммарную длину контактных линий; для прямозубых передач =1.

- коэффициент расчетной нагрузки;

- коэффициент концентрации нагрузки по ширине зубчатого венца, -коэффициент динамичности нагрузки; определяются из табл.1.6, табл.1.7 и формулой (1.6)

- коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых передач =1.

Таким образом МПа

Выполним проверочный расчет зубьев по напряжениям изгиба. По табл.1.10 в зависимости от

определяем

Вычисляем отношения

; ;

Расчет ведем по материалу шестерни, т.к.

Считаем:

МПа;

где - коэффициент формы зуба;

- коэффициент, учитывающий перекрытие зубьев, для прямозубых передач =1;

- коэффициент, зависящий от угла наклона зубьев,

;

- коэффициент расчетной нагрузки;

- коэффициент концентрации нагрузки по ширине зубчатого венца, -коэффициент динамичности нагрузки; определяются табл.1.6, табл.1.7 и формулой (1.6)

- коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых передач =1.

Таким образом

=218.23 МПа.

КПД цилиндрической передачи:

или 85%

где - поправочный коэффициент, учитывающий влияние нагрузки на КПД;

- коэффициент перекрытия, =1.5;

- коэффициент трения, =0.6.

Считаем для передачи 

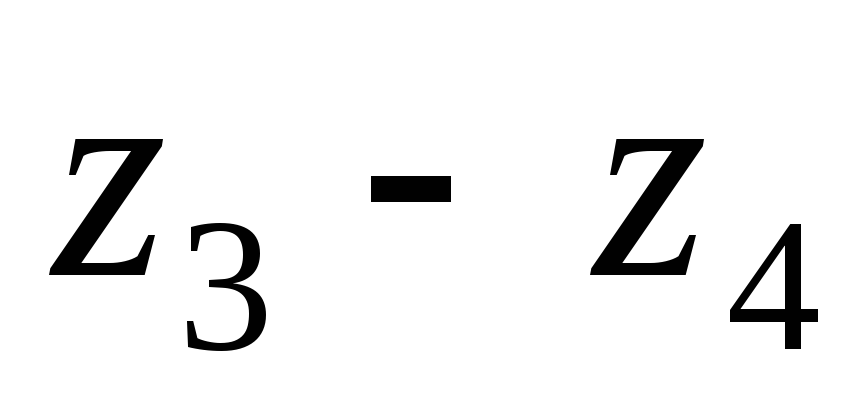
Параметры передачи необходимые для расчета:

Число зубьев: шестерни -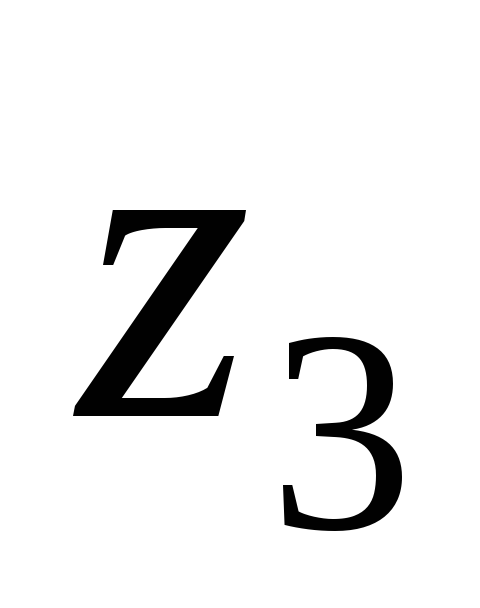=18, колеса -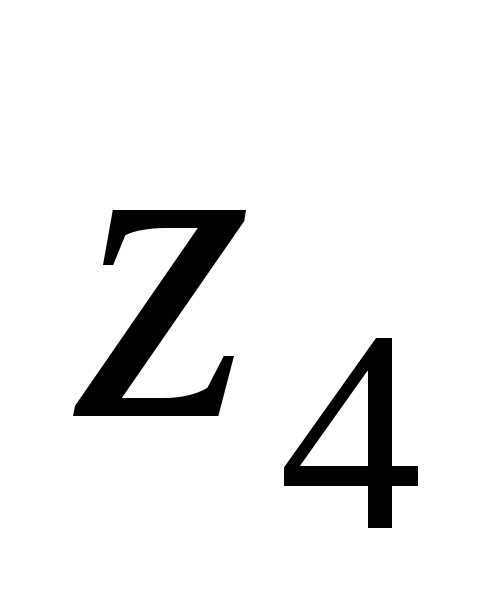=48.
Передаточное число =2.67.
Межосевое расстояние =13.2 мм.
Модуль передачи =0.4.
Момент на ведомом колесе:

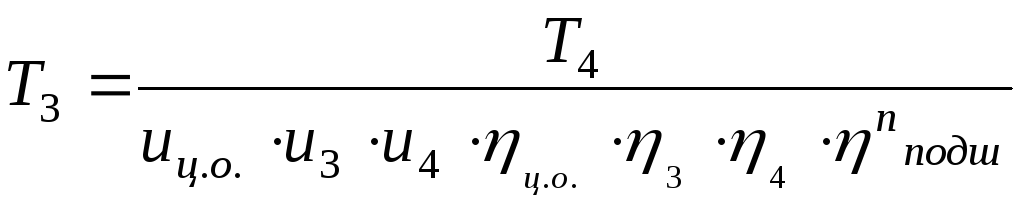
H м

Где - КПД 1-й пары подшипников качения,

- число пар подшипников,

- передаточное число открытой цилиндрической передачи,

- КПД открытой цилиндрической передачи.

материалы зубчатых колес:

шестерни – сталь 40X (улучшение), твердостью HB₃=270,

колеса – сталь 40X (улучшение), твердостью HB₄=260.

Допускаемые контактные напряжения 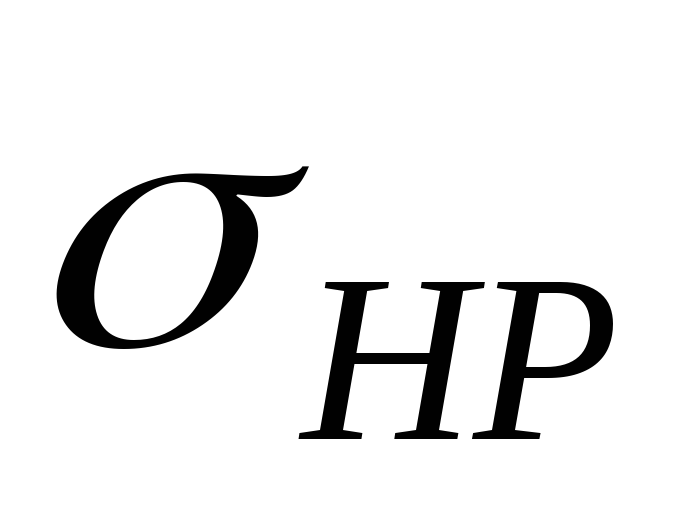для шестерни и колеса по формуле(7.7) и табл. 7.3.

для шестерни:

MПа,

MПа;

где - базовый предел контактной выносливости;

- коэффициент безопасности, для равномерной структуры (улучшение) =1.1.

для колеса:

MПа,

MПа;

В качестве расчетного допускаемого напряжения принимаем меньшее из двух, т.е. - =536 MПа.

Допускаемые напряжения изгиба по формуле (7.3) и табл.7.4:

для шестерни: MПа;

=260+ HB₃= 260+270=530 МПа;

для колеса: MПа;

=260+ HB₄= 260+260=520 МПа;

где - базовый предел выносливости зубьев по излому(в зависимости от материала и термообработки);

- коэффициент безопасности;

- коэффициент, учитывающий влияние реверсивности приложения нагрузки;

Определяем диаметры делительных окружностей:

шестерни: 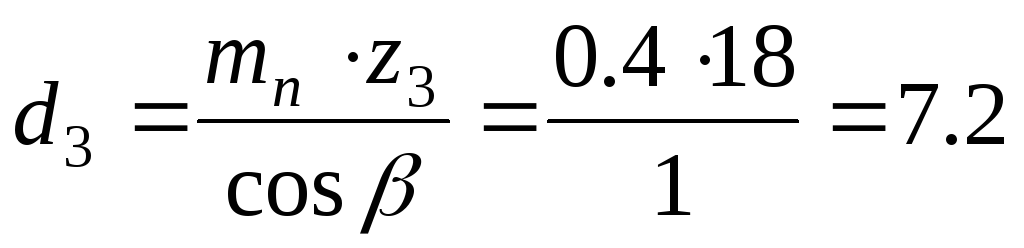мм
колеса: 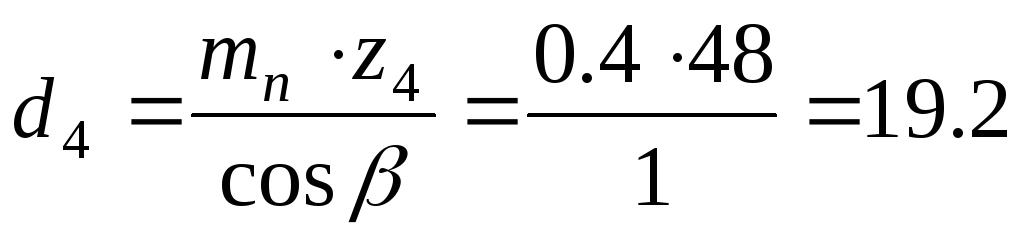мм.

Окружное усилие в зацеплении:

Считаем 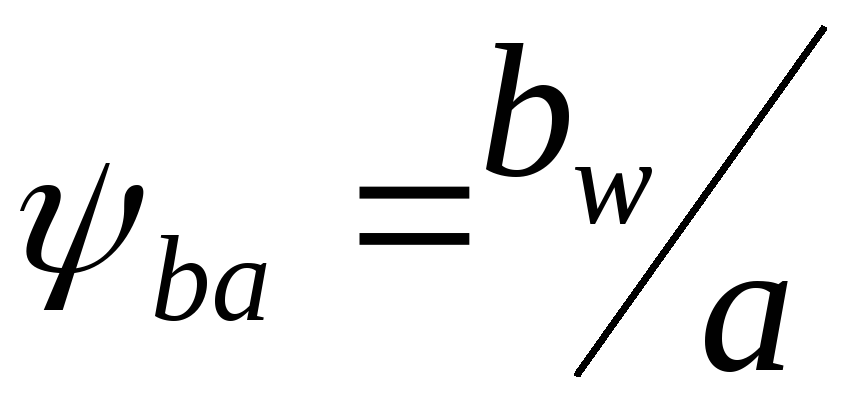-коэффициент ширины зубчатого венца колеса относительно межосевого расстояния. По табл. 1.8 определяем 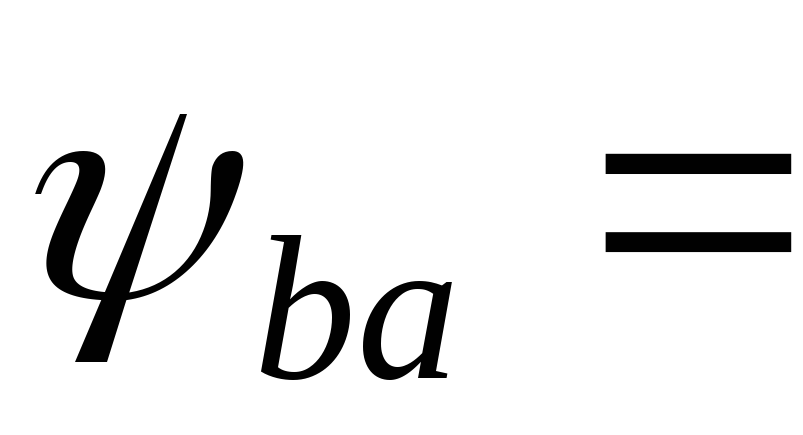0.3и определяем расчетную ширину колес:

мм

по принимаем 4 мм.

Фактическое контактное напряжение:

МПа

- коэффициент, учитывающий механические свойства материалов сопряженных колес; для стальных колес =275 МПа;

- коэффициент, учитывающий суммарную длину контактных линий; для прямозубых передач =1.

- коэффициент расчетной нагрузки;

- коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых передач =1.

Таким образом МПа

Выполним проверочный расчет зубьев по напряжениям изгиба. По табл.1.10 в зависимости от

определяем

Вычисляем отношения

; ;

Расчет ведем по материалу шестерни, т.к.

Считаем:

МПа;

где - коэффициент формы зуба;

- коэффициент, учитывающий перекрытие зубьев, для прямозубых передач =1;

- коэффициент, зависящий от угла наклона зубьев,

;

- коэффициент расчетной нагрузки;

- коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых передач =1.

Таким образом

=218.23 МПа.

КПД цилиндрической передачи:

или 60%

где - поправочный коэффициент, учитывающий влияние нагрузки на КПД;

- коэффициент перекрытия, =1.5;

- коэффициент трения, =0.6.

Считаем для передачи 

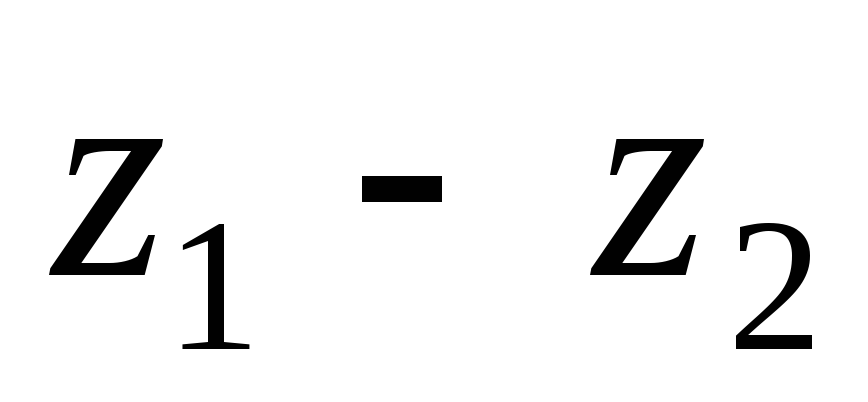
Параметры передачи необходимые для расчета:

Число зубьев: шестерни -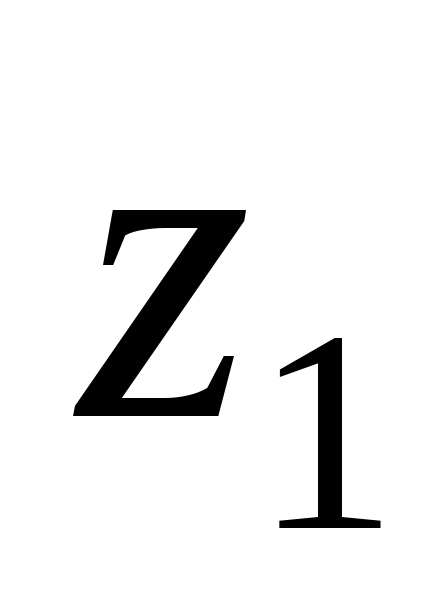=9, колеса -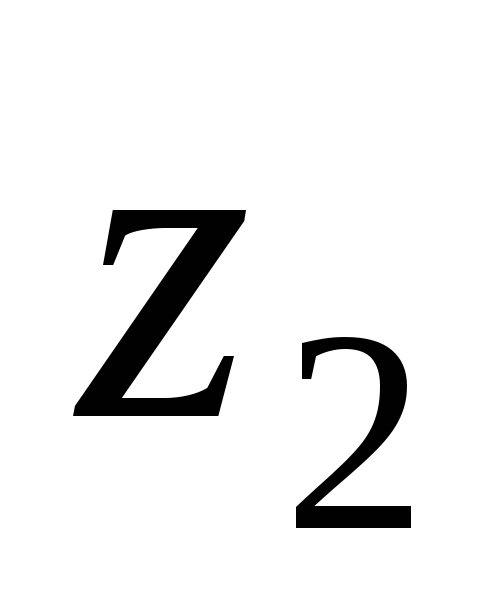=51.
Передаточное число =5.67.
Межосевое расстояние =12 мм.
Модуль передачи 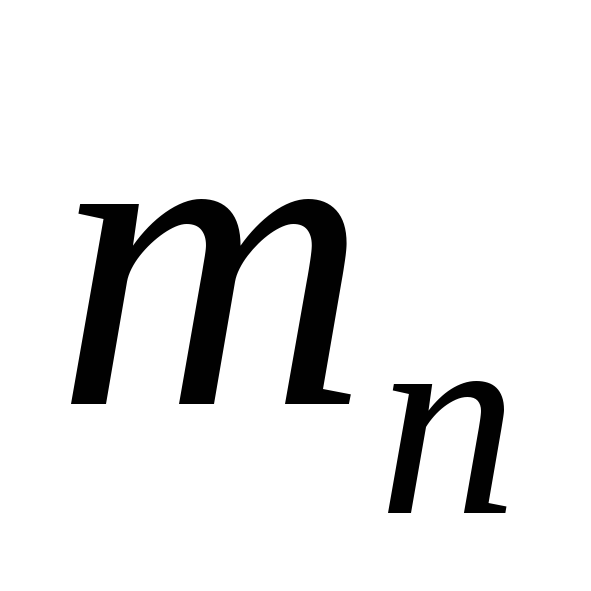=0.4.
Момент на ведомом колесе:

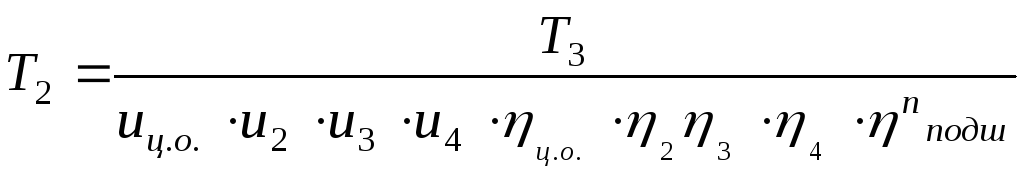
H м

Где - КПД 1-й пары подшипников качения,

- число пар подшипников,

- передаточное число открытой цилиндрической передачи,

- КПД открытой цилиндрической передачи.

материалы зубчатых колес:

шестерни – сталь 40X (улучшение), твердостью HB₁=270,

колеса – сталь 40X (улучшение), твердостью HB₂=260.

Допускаемые контактные напряжения 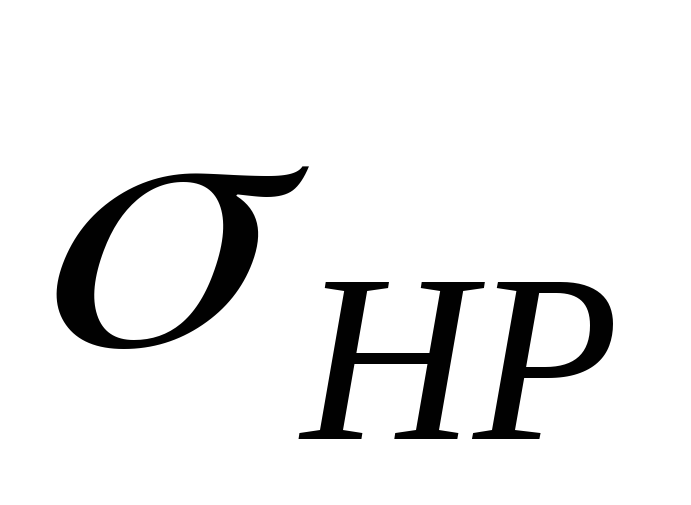для шестерни и колеса по формуле(7.7) и табл. 7.3.

для шестерни:

MПа,

MПа;

где - базовый предел контактной выносливости;

- коэффициент безопасности, для равномерной структуры (улучшение) =1.1.

для колеса:

MПа,

MПа;

В качестве расчетного допускаемого напряжения принимаем меньшее из двух, т.е. - =536 MПа.

Допускаемые напряжения изгиба по формуле (7.3) и табл.7.4:

для шестерни: MПа;

=260+ HB₁= 260+270=530 МПа;

для колеса: MПа;

=260+ HB₂= 260+260=520 МПа;

где - базовый предел выносливости зубьев по излому(в зависимости от материала и термообработки);

- коэффициент безопасности;

- коэффициент, учитывающий влияние реверсивности приложения нагрузки;

Определяем диаметры делительных окружностей:

шестерни: 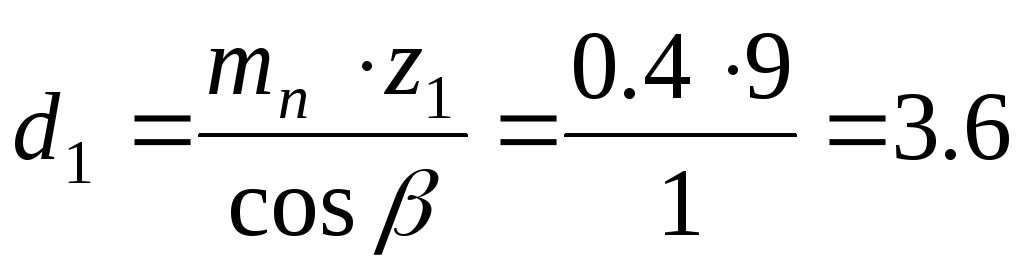мм
колеса: 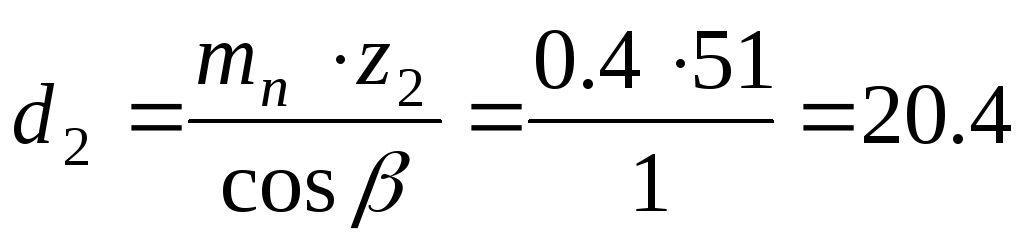мм.

Окружное усилие в зацеплении:

Считаем 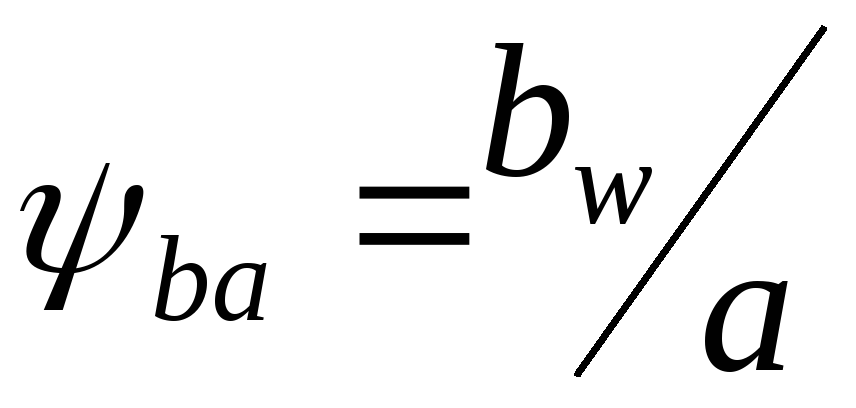-коэффициент ширины зубчатого венца колеса относительно межосевого расстояния. По табл. 1.8 определяем 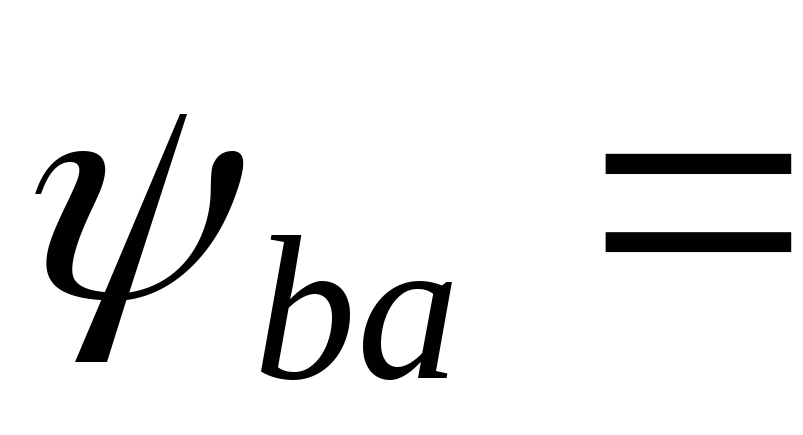0.25и определяем расчетную ширину колес: