2.4. Расчет элементов оптической схемы перестраиваемого по длинам волн лазера на красителях в твердотельной матрице.

Элементы оптической схемы резонатора, их взаимное расположение и углы поворота должны обеспечивать заданный ТТ диапазон длин волн лазерного излучения.

2.4.1 Расчет величины поперечного смещения пучка при прохождении через активный элемент .

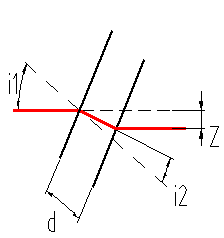
В соответствии с законами геометрической оптики, величина поперечного смещения пучка при прохождении через плоскопараллельную пластину (рис 2.7) определяется формулой [24] , (2.15)

Рис. 2.7 Поперечное смещение пучка в активном элементе

где d=8 мм – диаметр активного элемента, представляющего собой диск с плоскопараллельными поверхностями, а угол преломления определяется выражением sin i₁ = n × sin i₂ (для пластины в воздухе). Угол падения i₁ задается из соображений конструктивных особенностей резонатора и наименьших потерь на отражение, то есть должен быть близок к углу Брюстера для материала активного элемента – полиметилметакрилата (i₁47°).

Показатель преломления активного элемента также представляет собой постоянную величину для заданной длины волны и равен n1.496 для l580¸590 нм (диапазон длин волн, соответствующий максимуму излучения красителя родамина 6Ж). С изменением длины волны n меняется слабо, поэтому ограничимся расчетом Z для этого диапазона.

В связи с вышеизложенным и на основании формулы (2.15) получаем значение отклонения пучка в активном элементе от оси падения Z = 2.8 мм.

2.4.2. Расчет угловой ширины спектра при отклонении пучка призмой (блоком призм).

Отклонение пучка призмой зависит от длины волны падающего излучения, то есть определяется ее угловой дисперсией. Если призма установлена в условиях максимального отклонения, то луч проходит через призму симметрично и для 60°-й призмы i₁= -i₂ = =, а угловое расстояние между крайними лучами заданного спектрального диапазона (угловая ширина спектра) определяется формулой [25]:

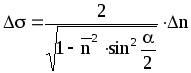, (2.16)

где a – угол при вершине призмы, Dn – разность показателей преломления материала призмы для крайних участков спектра, а –среднее значение показателя преломления в заданном диапазоне (см. рис 2.8).

Для 60°-й призмы (a=60°) формула (2.16) упрощается

При использовании в качестве материала призм вещества с большой дисперсией – тяжелого флинта (стекло ТФ-5) в заданном ТТ диапазоне спектра (550-750 нм) Dn=0,065 =1,755.

Расчет дает следующий результат: Ds = 0,143 рад (или 8°12¢) для одной призмы. При использовании блока из двух призм угловая ширина спектра удвоится, Ds = 16°24¢.

2.4.3. Определение габаритов глухого зеркала

Габариты глухого зеркала, поворотом которого осуществляется перестройка длины волны лазерного излучения, определяются угловой шириной спектра, разложенного призмой в заданном спектральном диапазоне (см. §2.4.2) и расстоянием от призмы до зеркала (рис. 2.8).

Из законов геометрической оптики легко получить следующую зависимость:

(2.17)

Результаты расчета по формуле (2.17) приведены в таблице 2.1.

Таблица 2.1

Зависимость габаритов глухого зеркала от его расположения

Расстояние до зеркала, l,мм	10	20	30	40
Смещение пучка, t,мм	2.8	5.8	8.6	11.5

Расчет проведен для блока из двух призм. При использовании одной призмы величина t будет в два раза меньше. Таким образом, при уменьшении расстояния от глухого зеркала до призмы его габариты могут быть уменьшены. В связи с этим, а также из конструктивных соображений, оптимальным расстоянием следует считать l = 20 мм.

Рис. 2.8. Определение габаритов глухого зеркала