2.3 Расчет оптического резонатора лазера накачки со стабильной каустикой

Оптическая накачка лазерных твердотельных активных элементов приводит к их внутреннему нагреву, который при наличии внешнего охлаждения обуславливает возникновение радиального температурного градиента с параболическим профилем распределения [21]. Внутри резонатора такой активный элемент действует как тонкая линза, оптическая сила которой изменяется пропорционально средней мощности накачки. При изменении оптической силы термической линзы активного элемента в общем случае изменяется мощность, расходимость и модовый состав излучения. Если подбором конфигурации резонатора выполнить условия стабильности каустики – пространственной формы заполнения объема резонатора электромагнитным полем вне зависимости от оптической силы внутрирезонаторной линзы, то в этом случае влияние тепловой линзы на выходные параметры может быть исключено или существенно уменьшено.

Рассмотрим резонатор, состоящий из двух зеркал произвольной кривизны R₁ и R₂, расположенных на расстояниях L₁ и L₂ от линзы с фокусным расстоянием F (рис. 2.6 а). С помощью известного преобразования данный резонатор может быть приведен к эквивалентному безлинзовому. Для этого необходимо зеркало с радиусом кривизны R₁, пространство L₁ и линзу F заменить на эквивалентное зеркало с кривизной R_Э и пространство L_Э (рис. 2.6 б) по формулам:

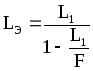
(2.6)

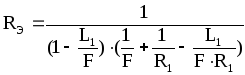
Такая замена не изменяет матрицу двойного прохода по резонатору и форму каустики на участке пространства L₂.

В случае больших чисел Френеля, когда можно пренебречь дифракцией излучения на апертурах зеркал, каустика поля основной моды имеет вид гауссова пучка с радиусом перетяжки w и радиусом кривизны волнового фронта r:

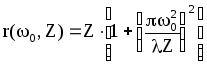, (2.7)

где z – расстояние вдоль оси пучка от перетяжки; l – длина волны излучения.

Как известно [22], гауссовы пучки реализуются только в устойчивых резонаторах, параметры которых удовлетворяют условию 0 < q1×q2 < 1. Это эквивалентно требованию самовоспроизводимости излучения при отражении от зеркал резонатора, необходимым условием выполнения которого является совпадение радиусов кривизны зеркал и волнового фронта пучка.

Применительно к рис. 2.6 б) условие самовоспроизводимости пучка при отражении от зеркал эквивалентного резонатора принимает вид:

(2.8)

При изменении оптической силы термической линзы эквивалентное зеркало меняет свое положение и кривизну. Если кривизна эквивалентного зеркала при его изменении будет все время совпадать с кривизной волнового фронта исходного гауссового пучка, то каустика резонатора останется неизменной.

Математическое условие стабильности каустики можно записать в виде:

; (2.9)

после подстановки всех значений получаем:

, (2.10)

где

Для определения геометрии резонатора со стабильной каустикой необходимо вначале построить эквивалентный резонатор, удовлетворяющий уравнению стабильности каустики, а затем подвергнуть его эквивалентную часть обратному преобразованию.

Выберем вначале гауссов пучок с нужным размером перетяжки w₀, задав тем самым полную расходимость пучка излучения и конфокальный параметр Z₀. Радиус кривизны эквивалентного зеркала R_Э, размещенного на расстоянии Z_Э от перетяжки, определяется условием самовоспроизводимости пучка при отражении. Длина эквивалентной части резонатора находится из уравнения стабильности (2.10):

(2.11)

Построение эквивалентного резонатора завершается установкой оси пучка выходного зеркала. Его расположение относительно линзы может быть в принципе произвольным, а радиус кривизны определяется условием самовоспроизводимости пучка при отражении.

В результате обратного преобразования определяются параметры резонатора L₁ и R₁:

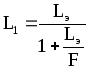
(2.12)

Очевидно, что различным значениям задаваемых величин Z_э и L₂ , будут соответствовать множество различающихся между собой резонаторов со стабильной каустикой. Однако, внимательный анализ взаимных зависимостей параметров R_э, L_э, R₂, L₂, Z₀, Z₂ позволяет получить несколько важных рекомендаций по выбору конкретных параметров резонатора.

Во-первых, хотя длина L₂ может быть выбрана произвольной, но для уменьшения габаритов излучателя выходное зеркало целесообразно размещать в непосредственной близости от линзы. Сушествует также минимальное из всех возможных значений L_э, которому соответствует минимум L₁. Для получения резонатора минимальных размеров эквивалентное зеркало следует размещать на расстоянии Z_э= -(-1)Z₀. Эквивалентная длина при этом равна L_э=2(-1)Z₀, а радиус кривизны эквивалентного зеркала

R_э = -2×Z₀.

Важным параметром является также и размер каустики на линзе, характеризующий заполнение активного элемента ТЭМ₀₀ -моды и энергетику выходного излучения. Величина его связана с другими параметрами соотношением:

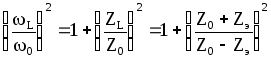(2.13)

Минимальному заполнению активного элемента (w_L / w₀ = 1) соответствует случай , когда зеркало R_э установлено на расстоянии Z_э = -Z₀. Перетяжка при этом находится на линзе. В области Z_э< -Z₀ перетяжка пучка находится вне эквивалентной части резонатора. При R2® (плоско-сферический резонатор) перетяжка пучка на линзе ограничивается величиной w_L <w₀. Располагая эквивалентное зеркало в области Z_э > 0, можно добиться любого желаемого заполнения активного элемента, так так при Z_эZ₀ размер пучка на линзе быстро возрастает, обращаясь в бесконечность при Z_э = Z₀. Этот случай соответствует отражающей точке (R₁0), расположенной в фокусе внутренней линзы (L₁F) [23].

Для оптимизации резонатора следует выбирать области, где выполняются условия

(2.14)