Лекция 16. Автономная нормальная система двух линейных дифференциальных уравнений. Фазовые траектории, фазовый портрет. Понятие об устойчивости точки покоя системы

Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.

В теории автономных систем принято обозначать независимую переменную буквой t, а

искомое решение — .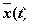

Ограничимся случаем n = 2 и в дальнейшем рассматриваем автономные системы второго порядка:

Будем полагать, что правые части системы f1(x1, x2 ) , f2(x1, x2) непрерывно

дифференцируемы в области 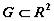, т.е. справедлива теорема существования и единственности. Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dt зависят только от x1 и x2. Автономные системы называют также динамическими системами.

Пусть x1=j1(t), x2= j2(t) — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Для n >2 фазовые траектории располагаются в фазовом пространстве.

Если на рисунке изображено несколько фазовых кривых системы, характеризующих качественное поведение решений системы (кривые с одинаковыми асимптотами, предельными точками и пр.), то такое изображение называется фазовым портретом системы.

Интегральные кривые рассматриваемой системы изображаются в трехмерном пространстве переменных (t, x1, x2) и, если x1=f1(t), x2= f2(t) — решение системы, то интегральная кривая задается в параметрической форме уравнениями

а фазовая траектория — не что иное, как проекция интегральной кривой на фазовую плоскость (плоскость (x1, x2).

ПРИМЕР 1. Фазовые кривые автономной системы.

92

Для фазовых кривых (фазовых траекторий) автономной системы с непрерывно дифференцируемой правой частью

, ,

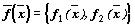справедливы следующие утверждения:

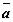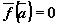·Если существует такая точка , что , то 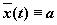, является решением автономной системы, т.е. соответствующая фазовая траектория — точка.

·Если точка (x1(t), x2(t)) принадлежит некоторой фазовой кривой, то при любой постоянной С точка (x1(t+С), x2(t+С)) принадлежит той же фазовой кривой.

·Две фазовые кривые либо не имеют общих точек, либо совпадают.

·Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор).

·Всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.

·Если фазовая кривая, отвечающая решению 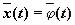, есть гладкая замкнутая кривая, то это решение — периодическая функция.

ПРИМЕР 2. Типы фазовых кривых.

Точка 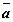, в которой правая часть системы обращается в нуль,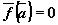, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.

ПРИМЕР 3. Точки покоя автономной системы.

Если в каждой точке области 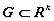задан n-мерный вектор

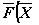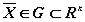,, то говорят, что в области G задано векторное поле. Запишем автономную систему второго порядка

в векторной форме:

где

,

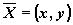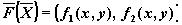
Автономная система

полностью определяется заданием векторного поля

.

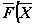Действительно, в каждой точке

гладкой фазовой кривой

существует касательный вектор

93

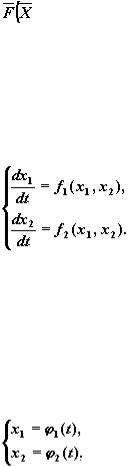
(x'(t0 ), y'(t0 ))

равный (в силу системы) вектору

,

иными словами, векторное поле

автономной системы задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.

Точки векторного поля, в которых вектор — нулевой, называют особыми точками векторного поля. Таким образом, точки покоя автономной системы — это особые точки векторного поля.

Рассмотрим автономную систему второго порядка:

Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1 /dt и dx2 /dt зависят только от x1 и x2 и не зависят от t.

Обозначим

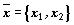и .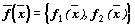

Пусть — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости 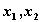. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы.

Точка 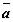, в которой правая часть системы обращается в нуль, 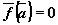, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.

Точка покоя называется устойчивой по Ляпунову, если:

1)существует такое , что для 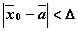при существует решение задачи Коши с начальным условиям ;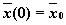

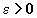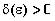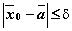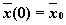2)для всякого существует такое , что если и , то

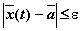при всех .

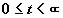Устойчивая точка покоя называется асимптотически устойчивой, если 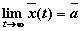при достаточно малых .

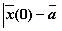94

Очевидно, что линейная автономная система

имеет единственную точку покоя: x1(t) = 0, x2(t) = 0, при всех 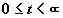. При этом характер точки покоя (0, 0) (ее устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по значениям собственных чисел l1 и l2 матрицы системы.

Аименно, пусть l1 и l2 — собственные значения матрицы A исследуемой системы:

·если l1 и l2— действительные отрицательные числа, то точка покоя устойчива и называется устойчивым узлом (пример 1);

·если l1 и l2 — действительные положительные числа, то точка покоя неустойчива и называется неустойчивым узлом (пример 2);

·если l1 и l2 — действительные числа, имеющие разные знаки, то точка покоя неустойчива и называется седлом (пример 3);

·если l1 и l2 — комплексные числа, l1,2 =Rell ± Imll и Rel не превышает нуля, то точка покоя устойчива, точнее, при Rel =0 точка устойчива, но не асимптотически устойчива и называется центром (пример 4), при Rel< 0 она асимптотически устойчива и называется устойчивым фокусом (пример 5), а если Rel>0, то точка покоя неустойчива и называется неустойчивым фокусом (пример 6);

·если l1 = l2 - отличные от нуля действительные числа, то точка покоя — узел специального вида, называемый диакритическим, устойчивым при отрицательных l1 = l2 и неустойчивым при положительных l1 = l2 (пример 7);

·если l1 = 0 и l2 № 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя (пример 8);

·если l1 = l2 = 0, то все точки плоскости являются точками покоя.

Пример 1. Поведение решений в окрестности устойчивого узла

Рассмотрим автономную систему

ее собственные значения l1 = -1 и l2 = -2 — отрицательные действительные числа. Следовательно, точка покоя (0, 0) — устойчивый узел.

Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

95

Пример 2. Поведение решений в окрестности неустойчивого узла

Рассмотрим автономную систему

ее собственные значения l1 = 1.5 и l2 = 0.5 — положительные действительные числа. Следовательно, точка покоя (0, 0) — неустойчивый узел. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

96

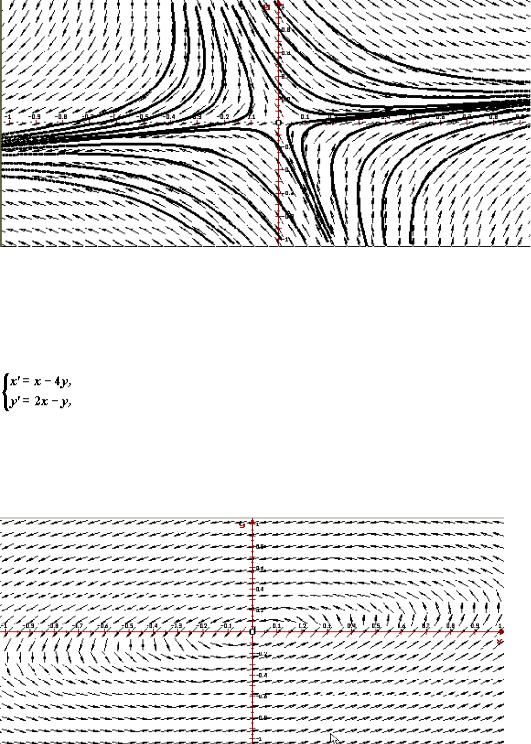
Пример 3. Поведение решений в окрестности седла

Рассмотрим автономную систему

ее собственные значения

,

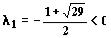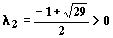
— действительные числа разных знаков. Следовательно, точка покоя (0, 0) — неустойчива, седло. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

97

Пример 4. Поведение решений в окрестности центра

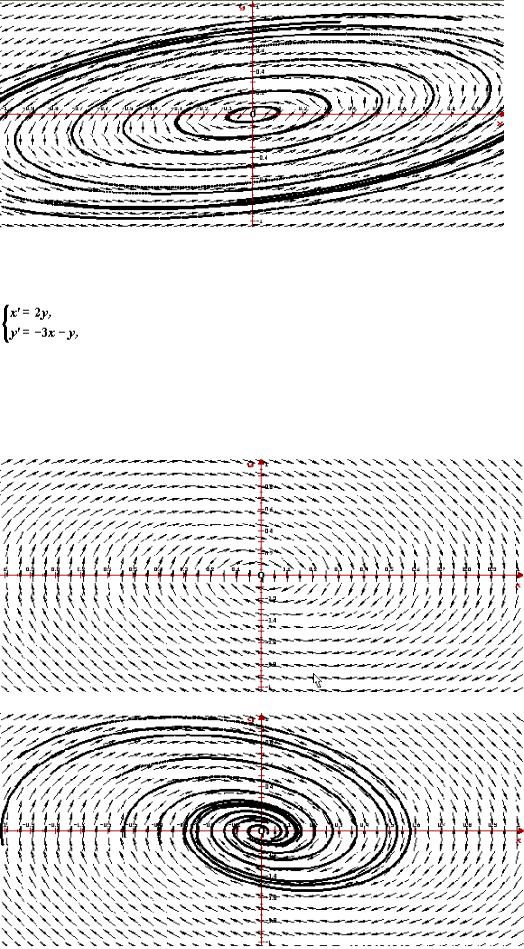
Рассмотрим автономную систему

ее собственные значения 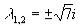— мнимые числа. Следовательно, точка покоя (0, 0)

— центр, устойчивая, но не асимптотически устойчивая точка покоя. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

98

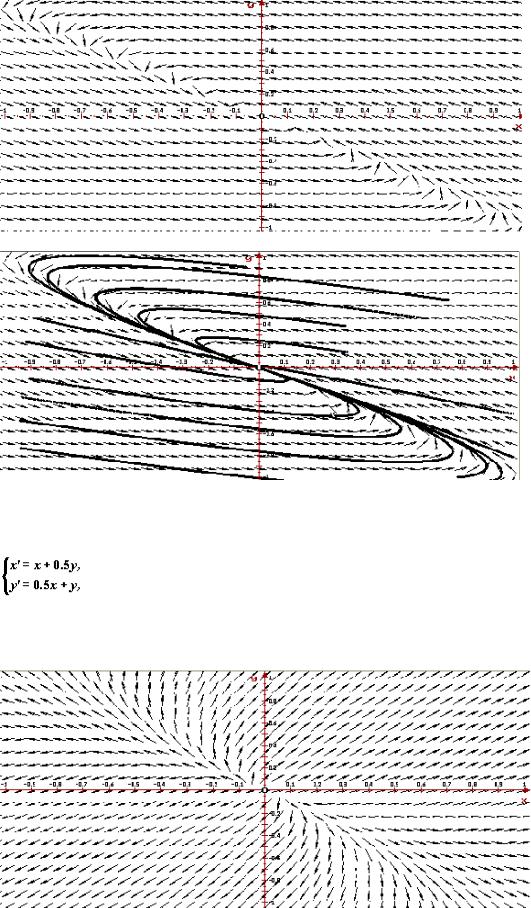
Пример 5. Поведение решений в окрестности устойчивого фокуса

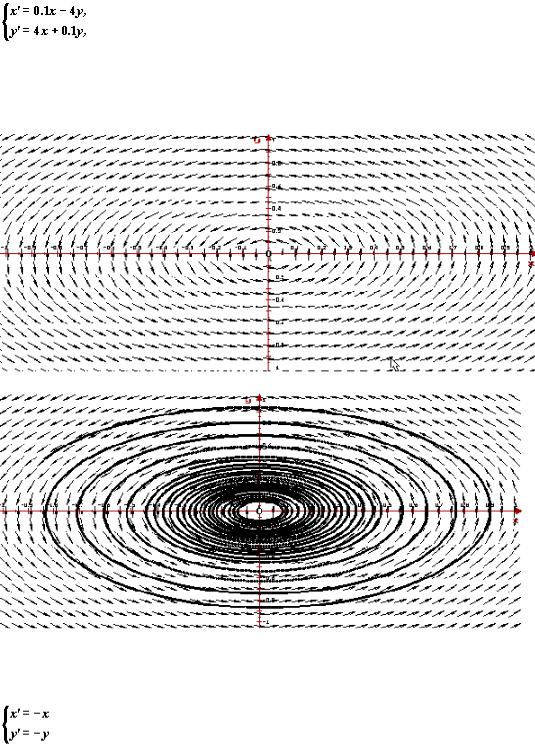
Рассмотрим автономную систему

ее собственные значения 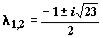— комплексные числа с отрицательными действительными частями. Следовательно, точка покоя (0, 0) — устойчивый фокус. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

99

Пример 6. Поведение решений в окрестности неустойчивого фокуса

Рассмотрим автономную систему

ее собственные значения l1 = 0.1+4 i и l2 = 0.1-4 i — комплексные числа с положительными действительными частями. Следовательно, точка покоя (0, 0) — неустойчивый фокус. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Пример 7. Поведение решений в окрестности диакритического узла

Рассмотрим автономную систему

ее собственные значения l1 = l2 = -1 — одинаковые действительные числа. Следовательно, точка покоя (0, 0) — устойчивый диакритический узел. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

100

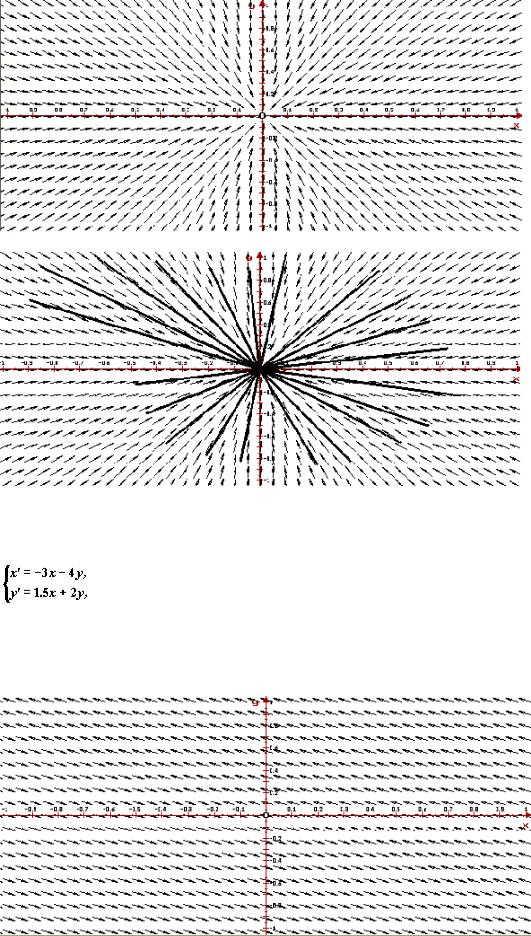
Пример 8. Автономная система с бесконечным множеством точек покоя

Рассмотрим автономную систему

ее собственные значения l1 = 0 и l2 = 1. Следовательно система имеет бесконечное множество точек покоя, расположенных на прямиой 3x+4y=0. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

101