
- •Лекция 2. Дифференциальные уравнения высшего порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл. Методы понижения порядка дифференциального уравнения
- •Лекция 4. Неоднородные линейные дифференциальные уравнения. Структура общего решения. Принцип суперпозиции решения. Метод Лагранжа вариации произвольных постоянных
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера решения однородных уравнений. Метод подбора неоднородных уравнений
- •Лекция 6. Комплексные числа, последовательности комплексных чисел
- •Лекция 7. Функции комплексной переменной. Предел. Непрерывность. Дифференцирование функции комплексной переменной. Понятие аналитической функции комплексной переменной
- •Лекция 8. Ряды с комплексными числами. Степенные ряды. Элементарные функции комплексной переменной
- •Лекция 9. Интеграл от функции комплексной переменной по кривой на комплексной плоскости. Интеграл от аналитической функции. Формула Ньютона-Лейбница
- •Лекция 10. Интегральная формула Коши. Интегральная теорема Коши. Теоремы Морера и Лиувилля. Разложимость аналитической функции в степенной ряд. Ряд Тейлора
- •Лекция 11. Ряд Лорана. Теорема Лорана. Изолированные особые точки однозначной аналитической функции. Вычет в изолированной особой точке
- •Лекция 12. Вычисление контурных интегралов с помощью вычетов
- •Лекция 13. Основные понятия операционного исчисления. Преобразование Лапласа, его свойства
- •Лекция 14. Обращение преобразования Лапласа (формула Меллина). Восстановление оригиналов по известным изображениям. Решение дифференциальных уравнений операционным методом
- •Лекция 16. Автономная нормальная система двух линейных дифференциальных уравнений. Фазовые траектории, фазовый портрет. Понятие об устойчивости точки покоя системы
Лекция 14. Обращение преобразования Лапласа (формула Меллина). Восстановление оригиналов по известным изображениям. Решение дифференциальных уравнений операционным методом
Теорема 13.5 (Меллина).} Пусть F ( p) ÎC ¥ (Re p > a) и
1) | F ( p) |= 0 |
при| p |® ¥ , Re p > a относительно аргумента; |
|||||||||||||||||
2) для "x > a интеграл |
|
|
|
|
|
|
|
|
||||||||||
|
x+i¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ò | F( p) | dy<M равномерно ограничен по |
x . |
|
|||||||||||||||
|
x-i¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда существует |
f (t)ÎA(a): f (t) B F ( p) и |
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
x+i¥ |
|
|
|
|
|
|
|
|
|
|
|
|
f (t) = |
ò e pt F ( p)dp для любого x > a . } |
|
|
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
2pi x-i¥ |
|
|
|
|
|
|
|
|
|
|
||
|
Замечание. Несобственный интеграл |
|
|
|||||||||||||||
1 |
|
x+i¥ |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ò e pt F ( p)dp вычисляется вдоль прямой Re p = x > a и понимается в смысле |
|||||||||||||||||
|
|
|
|
|||||||||||||||
|
2pi x-i¥ |
|
|
|
|
|
|
|
|
|
|
|
||||||
главного значения: |
|
|
|
|
|
|
|
|
|
|||||||||
|
x+i¥ |
|
|
|
x+iA |
|
|
|
|
|
|
|
|
|||||
ò |
e pt F ( p)dp = limA®¥ ò e pt F ( p)dp. |
|
|
|
||||||||||||||
|
x-i¥ |
|
|
|
x-iA |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Изображение произведения |
||||||
Пусть |
f1 (t) Î A(a1 ): f1 (t) B F1 ( p) ÎC ¥ (Re p > a1 ), f2 (t) Î A(a2 ): f2 (t) B F2 ( p) ÎC¥ (Re p > a2 ). |
|||||||||||||||||
Функция |
f (t) = f1 (t) f2 (t) Î A(a1 + a2 ) |
удовлетворяет всем условиям существования |
||||||||||||||||
изображения. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
f (t) B F( p) = òe- pt f1 (t) f2 (t)dt = |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
= á f=(t) |
1 |
x+i¥ e pt |
F ( p)dp для "x > a ñ = |
|
|
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
2pi |
ò |
1 |
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
x-i¥ |
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
¥ |
|
x+i¥ |
|
|
|
|
1 |
|
x+i¥ |
¥ |
|
||
= |
|
|
òe- pt f2 (t) ò eqt F1 (q)dqdt = |
|
ò F1 (q)òe-( p-q)t f2 (t)dtdq = |
|||||||||||||
2pi |
2pi |
|||||||||||||||||
|
|
0 |
|
x-i¥ |
|
|
|
|
x-i¥ |
0 |
|
|||||||
|
|
1 |
|
x+i¥ |
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
ò F1 (q)F2 ( p - q)dq. |
|
|
|
|
|
|
||||||||||
2pi |
|
|
|
|
|
|
||||||||||||
|
|
x-i¥ |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
x+i¥ |
|
|
|
||||
|
a1 < x Req < Re=p - a2 |
ò F=1 ( p - q)F2 (q)dq; |
||||||||||||||||
|
|
2pi |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x-i¥ |
|
|
|
||||
|
a |
< x =Req < Re p - a ; |
F ( p) ÎC¥ (Re p > a + a |
. |
||||||||||||||
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
||
Пример 13.2.
78

f (t) = t B |
1 |
; |
f |
|
(t) = sin(wt) B |
|
w |
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
p2 |
+w2 |
|
|
|
|
|
|
|
||||||||||||||||
1 |
p2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
x+i¥ |
|
|
dq |
|
|
|
|
|
||
f (t) = f1 (t) f2 (t) = t sin(wt) |
B |
|
|
ò |
|
|
|
|
|
|
|
|
|
; |
||||||||||||
|
|
|
( p |
- q) |
2 |
(q |
2 |
+w |
2 |
) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pi x-i¥ |
|
|
|
|
||||||||
= -w Выч= |
é |
= |
|
|
|
|
1 |
|
|
|
|
, q |
|
p |
ù |
(при помощи вычетов, с учетом того что контур |
||||||||||
ê |
|
|
|
2 |
(q |
2 |
|
2 |
) |
|
ú |
|||||||||||||||
|
ë |
( p - q) |
|
|
+w |
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
||||||
интегрирования замыкается вправо и обходится по часовой стрелке --- в отрицательном направлении)
= -w Выч= |
é |
= |
|
1 |
|
|
|
|
, q |
ê |
2 |
(q |
2 |
+w |
2 |
) |
|||
|
ë |
( p - q) |
|
|
|
||||
p |
ù |
|
wd |
é |
|
|
1= |
|
, q |
ú |
= - |
= |
|
|
|
||||
|
|
2 |
2 |
||||||
|
|
dq |
ê |
|
+w |
|
|||
|
û |
|
ë q |
|
|
|
|||
ù |
2w p |
|
|
||
pú |
|
|
|
|
. |
p |
2 |
+w |
2 |
||
û |
|
|
|
||
Указание: можно считать контур интегрирования замкнутым налево и суммировать вычеты в ±iw.
Теоремы свертки и запаздывания.
Теорема. (теорема запаздывания) Если f(t) = 0 при t < 0, то справедлива формула
L[ f (t - t0 )] = e - pt0 L[ f (t)]
где t0 – некоторая точка.
t
Определение. Выражение ò f1 (t) f2 (t - t)dt называется сверткой функций f1(t) и f2(t) и
0
обозначается f1* f2.
Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций f1(t) и f2(t) .
· t
F1 ( p)F2 ( p) =· ò f1 (t) f 2 (t - t)dt
0
Теорема. (Интеграл Дюамеля (Дюамель (1797 – 1872) – французский математик)). Если
··
F ( p) = f (t); G( p) = g(t) , то верно равенство
··
|
|
|
· |
|
t |
|
¢ |
|
|
|
|
|
|
|
· |
|
ò |
|
|
|
|
|
|
|
|
|
pF ( p)G( p) = f (t)g(0) + |
|
f (t)g (t - t)dt |
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для |
нахождения |
изображений |
различных |
функций |
наряду |
с |
непосредственн |
||||
интегрированием применяются приведенные выще теоремы и свойства. |
|
|
|||||||||
Пример. Найти изображение функции sin t . t
79
|
|
|
|
|
|
|
|
|
|
|
|
· |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из таблицы изображений получаем: sin t = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
· |
p 2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) |
· ¥ |
|
|
|
|
|
|
|
|
|
|||
По свойству интегрирования изображения получаем: |
|
|
=· òF(q)dq |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
t |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||
|
|
|
sin t · ¥ |
|
1 |
|
|
¥ |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
=· ò |
|
|
|
|
|
dq = arctgq |
|
= |
|
|
|
|
- arctgp; |
|
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
q |
2 |
+1 |
p |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример. Найти изображение функции sin 2 t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Из тригонометрии известна формула sin 2 t |
= |
1 - cos 2t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
· |
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
p |
|
|
p |
2 |
+ 4 - p |
2 |
|
2 |
|
|
||
Тогда sin 2 t = |
L[1 - cos 2t] = |
L[1] - |
L[cos 2t] = |
- |
|
|
|
|
|
|
= |
|
|
= |
|
. |
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p( p 2 |
+ 4) |
|||||||||||||||||||
· 2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 p 2( p 2 |
+ 4) 2 p( p 2 + 4) |
|
|||||||||||||||||||||
Операционное исчисление используется как для нахождения значений интегралов, так и для решение дифференциальных уравнений.
Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.
|
an x (n) (t) + ... + a1 x¢(t) + a0 x(t) = f (t) |
|
Требуется найти |
решение этого дифференциального уравнения, удовлетворяющее |
|
начальным условиям: |
|
|
|
x(0) = x0 ; x¢(0) = x0¢ ; ... |
x (n-1) (0) = x0(n -1) . |
Если функция x(t) |
является решением этого |
дифференциального уравнения, то оно |
обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция f(t) имеет (по теореме единственности) одно и то же изображение Лапласа.
é n |
d |
k |
x |
ù |
|
Lêåak |
|
ú |
= L[ f (t)] |
||
dt |
k |
||||
ëk =0 |
|
û |
|
||
|
|
|
|
|
|
|
. |
Из теоремы |
|
о |
|
¢ |
|||
|
|
дифференцировании оригинала{ pF ( p) - f (0) = f (t) } можно сделать |
|||||
|
|
|
|
|
|
|
. |
|
|
é |
d |
k |
ù |
|
|
вывод, что Lê |
|
x |
ú |
= p k L[x] - p k -1 x(0) -... - px(k -2) (0) - x (k -1) (0). |
|||
|
|
k |
|||||
|
|
ë dt |
|
û |
|
||
é |
d |
n |
ù |
|
|
|
|
Тогда an Lê |
x |
ú |
+ ... + a0 L[x] = L[ f ]. |
||||
|
n |
||||||
ë dt |
û |
|
|
|
|||
80
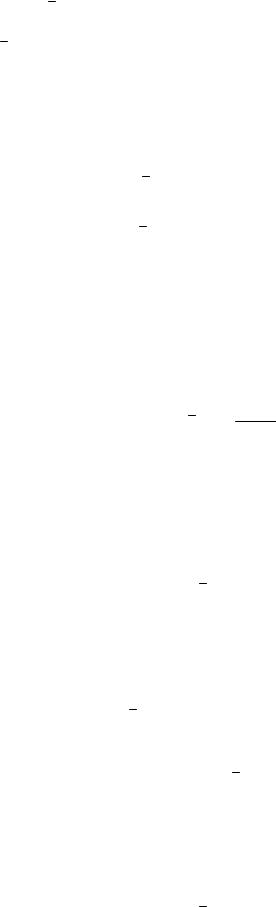
Обозначим L[x] = |
x |
( p), |
L[ f ] = F ( p). |
|
|
|
|
|
|
|
||||||||||||
Получаем: |
x |
( p)[an p n + an-1 p n-1 + ... + a1 p + a0 ] = an [ p n-1 x0 + p n-2 x¢0 + ... + x0(n-1) ] + |
||||||||||||||||||||
|
|
|
|
+ an-1[ p n -2 x0 + p n-3 x0¢ + ... + x0(n -2 ) ] + .... + a2 [ px0 + x0¢ ] + a1 x0 |
+ F ( p). |
|||||||||||||||||
Это уравнение |
|
называетсявспомогательным (изображающим) |
или операторным |
|||||||||||||||||||
уравнением. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда получаем изображение |
x |
( p) , а по нему и искомую функцию x(t). |
||||||||||||||||||||
Изображение получаем в виде: |
x |
( p) = |
F ( p) |
+ |
Yn-1 ( p) |
|
|
|||||||||||||||
Rn ( p) |
Rn ( p) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Где R |
n |
( p) = a |
n |
p n |
+ a |
n-1 |
p n -1 + ... + a p + a |
0 |
; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
Yn-1 ( p) = a1 x0 |
|
+ a2 ( px0 |
+ x0¢ ) + a3 ( p 2 x0 |
+ px0¢ + x0¢¢) + ... + an ( p n-1 x0 + p n-2 x0¢ + ... + px0(n-2) + x0(n-1) ) |
||||||||||||||||||
Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:
x( p) = F ( p) Rn ( p)
Рассмотрим применение этого метода на примерах.
Пример. Решить уравнение y |
¢¢ |
+ 4 y = 2; |
¢ |
= 0. |
|
y(0) = y (0) |
Изображение искомой функции будем искать в виде:
|
|
|
y |
= |
F ( p) |
|
|
|
|
Rn ( p) |
|||
|
|
|
|
|
||
F ( p) = L[ f ] = L[2] = |
2 |
; |
|
Rn ( p) = 1× p 2 + 0 × p |
||
|
|
|||||
|
p |
|
|
|
|
|
y |
= |
|
2 |
|
= |
1 |
é 1 |
- |
|
|
p |
ù |
|
|
|
|
|
ê |
|
|
|
|
ú |
||||
p( p |
2 |
+ 4) |
2 |
|
p |
2 |
+ 4 |
||||||
|
|
|
|
ë p |
|
|
û |
||||||
· |
1 |
|
|||
Находим оригинал, т.е. искомую функцию: |
y |
= y = |
(1 - cos 2 |
||
2 |
|||||
· |
|
||||
|
|
||||
+ 4 = p 2 + 4.
x)
Пример. Решить уравнение y¢ - 2 y = 0; |
y(0) = 1. |
|
||
F ( p) = L[ f ] = L[0] = 0; |
|
Rn ( p) = p - 2; Yn-1 = a1 y0 = 1; |
||
|
y |
= |
1 |
; |
|
p - 2 |
|||
|
|
|
|
|
81
·
y = y = e2 x ;
·
Пример. Решить уравнение:
y |
¢¢¢ |
- 6 y |
¢¢ |
+ |
11y |
¢ |
- 6 y = 0; |
y(0) = 0; |
¢ |
= 1; |
¢¢ |
||||
|
|
|
y (0) |
y (0) = 0; |
|||||||||||
|
F ( p) = L[ f ] = L[0] = 0; |
Rn ( p) = p3 - 6 p 2 |
+11p - 6; |
||||||||||||
Yn-1 ( p) = a1 y0 + a2 ( py0 + y0¢ ) + a3 ( p 2 y0 + py0¢ + y0¢¢) = -6 + p. |
|||||||||||||||
Изображение искомой функции |
|
y |
= |
- 6 + p |
|
|
|
|
|||||||
|
|
|
|
|
|||||||||||
|
p3 - 6 p 2 +11p - 6 |
|
|
||||||||||||
Для нахождения |
оригинала |
необходимо |
разложить полученную дробь |
||||||||||||
элементарные дроби. Воспользуемся делением многочленов(знаменатель делится без остатка на p – 1):
p3 – 6p2 + 11p – 6 |
p - 1 |
|||||||
p3 – p2 |
|
|
|
|
|
|
p2 – 5p + 6 |
|
|
|
|
|
|
|
|
||
|
-5p2 |
+ |
11p |
|
||||
|
|
|||||||
|
-5p2 |
|
|
|
|
|
|
|
|
+ |
5p |
|
|
|
|
||
|
|
|||||||
6p - 6
6p - 6
0
В свою очередь p 2 - 5 p + 6 = ( p - 2)( p - 3)
Получаем: p3 - 6 p 2 +11p - 6 = ( p -1)( p - 2)( p - 3).
Тогда: |
y |
= |
- 6 + p |
= |
A |
+ |
B |
+ |
C |
; |
|
|
|
|
|||||||
|
|
|
p3 - 6 p 2 +11p - 6 p -1 p - 2 p - 3 |
|
||||||
Определим коэффициенты А, В и С.
A( p - 2)( p - 3) + B( p -1)( p - 3) + C( p -1)( p - 2) = -6 + p
Ap 2 - 5Ap + 6 A + Bp2 - 4Bp + 3B + Cp 2 - 3Cp + 2C = -6 + p
82

p 2 ( A + B + C) - p(5A + 4B + 3C) + 6 A + 3B + 2C = -6 + p |
|
|||||||
|
|
|
|
|
ì |
|
5 |
|
ìA + B + C = 0 |
|
ìC = -A - B |
ìC = -A - B |
ïA |
= - |
|
||
|
2 |
|||||||
ï |
+ 4B + 3C |
= -1 |
ï |
ï |
ï |
= 4 |
|
|
í5A |
í2A + B = -1 |
íB = -1 - 2A |
íB |
|
||||
ï |
+ 3B + 2C |
= -6 |
ï |
ï |
ï |
|
3 |
|
î6A |
î4A + B = -6 |
î2A -1 = -6 |
ï |
= - |
||||
|
|
|
||||||
|
|
|
|
|
C |
2 |
||
|
|
|
|
|
î |
|
||
|
|
|
11 - 6 p |
- |
5 |
|
|
4 |
|
- |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
y |
= |
= |
2 |
|
+ |
+ |
2 |
|
; |
||||
|
|
|
|
|
|
|||||||||
|
|
|
p3 - 6 p 2 +11p - 6 p -1 p - 2 p - 3 |
|
||||||||||
y = y = - 5 e x + 4e 2 x - 3 e3x ; |
||||||
· |
|
|
|
|
||
|
|
|
|
|
|
|
· |
2 |
2 |
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
Приемы операционного исчисления можно также использовать для решения систем дифференциальных уравнений.
Пример. Решить систему уравнений:
|
|
|
|
ìx¢ = 3x + 4 y |
; |
x(0) = y(0) = 1 |
í |
||||||
|
|
|
|
îy¢ = 4x - 3y |
|
|
Обозначим |
x |
( p), |
y |
( p) - изображения |
искомых функций и решим вспомогательные |
|
уравнения: |
|
|
||||
¢ |
|
ìL[x ] = 3L[x] + 4L[ y] |
|
í ¢ |
; |
îL[ y ] = 4L[x] - 3L[ y]
ìpx( p) - x(0) = 3x( p) + 4 y( p)
í
îpy( p) - y(0) = 4x( p) - 3y( p)
Решим полученную систему алгебраических уравнений.
ì |
x |
( p) = |
4 |
y |
( p) +1 |
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|||
|
p - 3 |
||||||||||||
ï |
|
|
|
|
|||||||||
í |
|
|
|
|
|
|
|
; |
|||||
ïpy |
( p) -1 = 4 |
4 |
y |
( p) +1 |
- 3 |
y |
( p) |
||||||
|
|
|
|||||||||||
ï |
|
|
|
|
|
|
|
p - 3 |
|||||
î |
|
|
|
|
|
|
|
||||||
ì
ïy( p)
ï
í
ïïx( p)
î
= p +1 p 2 - 25
=
;
p 2 + 4 p - 21
( p 2 - 25)( p - 3)
x |
( p) = |
( p + 7)( p - 3) |
= |
p + 7 |
= |
p |
+ |
7 |
; |
|
|
p 2 - 25 |
p 2 - 25 |
||||||
|
|
( p 2 - 25)( p - 3) |
p 2 - 25 |
|
|
||||
83

x( p) = x(t) = ch5t + 7 sh5t; |
|||||||
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
5 |
|
|
||
|
|
|
|
|
|
||
y |
( p) = |
p |
+ |
1 |
; |
||
|
|
||||||
p 2 - 25 |
p 2 - 25 |
||||||
y( p) = y(t) = ch5t + 1 sh5t; |
||
· |
|
|
|
|
|
· |
5 |
|
|
|
|
Если применить к полученным результатам формулы
chz = |
e z |
+ e- z |
|
; |
|
shz = |
e z - e- z |
; |
||||||||
|
2 |
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то ответ можно представить в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
6 |
|
|
|
5t |
|
1 |
|
|
-5t |
|
||
|
ïx = |
|
|
|
e |
|
- |
|
|
e |
|
|
|
|
||
|
|
5 |
|
|
5 |
|
|
|
|
|
||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
; |
|
||
|
í |
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
||
|
ï |
|
|
|
|
|
5t |
|
|
|
-5t |
|
||||
|
ïy = |
|
|
e |
|
+ |
|
|
e |
|
|
|
||||
|
5 |
|
|
5 |
|
|
|
|||||||||
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Как видно, гиперболические функции |
|
|
|
в |
|
|
|
ответе |
могут быть легко заменены |
|||||||
показательные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Решить систему уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx¢ = 5x + 2 y |
|
|
|
при x(0) = y(0) = 1 |
||||||||||||
í |
|
|
|
|
|
|
||||||||||
îy¢ = 2x + 2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составим систему вспомогательных уравнений:
¢ |
|
ìL[x ] = 5L[x] + 2L[ y] |
; |
í ¢ |
îL[ y ] = 2L[x] + 2L[ y]
ìpx |
( p) - x(0) |
= 5 |
x |
( p) + 2 |
y |
( p) |
||
í |
|
|
|
|
|
; |
||
îpy |
( p) - y(0) |
= 2 |
x |
( p) + 2 |
y |
( p) |
||
ì
ïx( p) =
ï
í
ïïpy( p)
î
2 y( p) +1
p - 5
;
= 4 y( p) + 2 + 2 y( p) +1 p - 5
ì
ïy( p)
ï
í
ïïx( p)
î
p - 3
=
( p -1)( p - 6);
p
=
( p -1)( p - 6)
y( p) = |
A + B = 2 1 + 3 1 = 2 et + 3 e6t ; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p -1 p - 6 5 p -1 5 p - 6 · 5 |
5 |
|
|
|
|||||||||||||||||||||||
x( p) = |
C + D = - |
1 1 + 6 1 =- 1 et + 6 e6t ; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
p -1 p - 6 |
5 p -1 5 p - 6 · 5 |
5 |
|
||||||||||||||||||||||||
84
Если обозначить C = - |
1 |
; |
C |
|
= |
3 |
; то из полученного частного решения системы можно |
||||||
|
2 |
|
|||||||||||
1 |
5 |
|
|
5 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
записать и общее решение: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ì |
t |
+ 2C2 e |
6t |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
ïx = C1e |
|
|
|
|||
|
|
|
|
|
|
|
í |
|
|
t |
|
|
6t |
|
|
|
|
|
|
|
ï |
|
|
+ C2 e |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
îy = -2C1e |
|
|
||||
При рассмотрении нормальных систем дифференциальных уравнений этот пример был решен традиционным способом(См. Другой способ решения.). Как видно, результаты совпадают.
Отметим, что операторный способ решения систем дифференциальных уравнений применим к системам порядка выше первого, что очень важно, т.к. в этом случае применение других способов крайне затруднительно.
85
Лекция 15. Системы дифференциальных уравнений. Задача Коши. Теорема существования и единственности решения задачи Коши.
Структура общих решений однородных и неоднородных
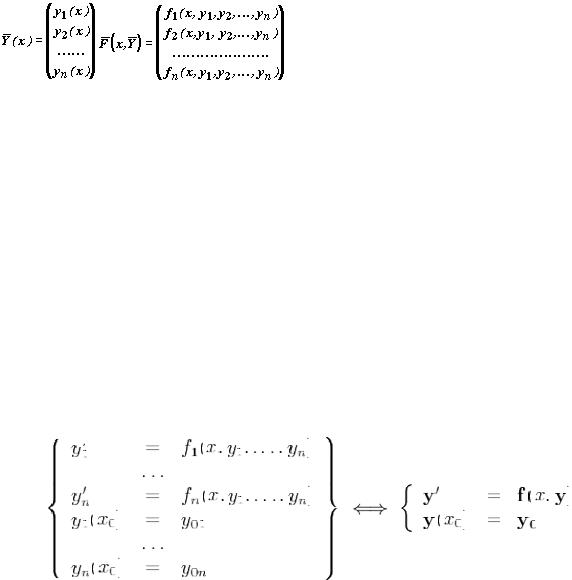
Рассмотрим систему дифференциальных уравнений
y'1 = f1(x, y1, y2 , ..., yn), y'2 = f2 (x, y1, y2 , ..., yn),
..............................
y'n = fn (x, y1, y2 , ..., yn),
где x — независимая переменная, а
y1(x), y2(x), ..., yn(x) — неизвестные функции, n — порядок системы.
Обозначив
запишем систему в векторной форме
`Y '=`F(x,`Y ).
Решением системы называется вектор-функция `Y , которая определена и нерерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех x0О (a, b) справедливо
`Y '(x) =`F(x,`Y (x)).
Задачей Коши (задачей с начальными условиями) называется следующая задача: найти такое решение`Y (x) системы `Y '=`F(x,`Y ), что `Y (x0) =`Y 0,
где x0 — заданное число, а `Y 0 — заданный вектор.
Интегральной кривой системы называется кривая в (n+1) -мерном пространстве Rn+1x,y, заданная уравнением `Y =`Y (x), где `Y (x) - решение системы.Таким образом, решить задачу Коши — это значит найти интегральную кривую, проходящую через заданную точку пространства Rn+1x,y.
·Система  ОДУ первого порядка, разрешённая относительно производных
ОДУ первого порядка, разрешённая относительно производных
(нормальная система  -го порядка)
-го порядка)
·ОДУ  -го порядка, разрешённое относительно старшей производной
-го порядка, разрешённое относительно старшей производной
86
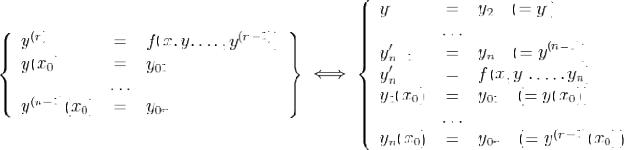
Для нормальных систем обыкновенных дифференциальных уравнений справедлива следующая
Теорема 15.1(теорема существования и единственности решения задачи Коши.)
Если вектор-функция `F(x,`Y (x)) и ее частные производные по переменным yi , i = 1, 2, ..., n, непрерывны в области G пространства Rn+1x,y, то на некотором интервале (x0 -h, x0+h) существует единственное решение системы
`Y '(x) =`F(x,`Y (x)) ,
удовлетворяющее начальному условию
`Y (x0) =`Y 0,
т.е. через каждую точку области G проходит единственная интегральная кривая системы.
Подробнее геометрическая интерпретация систем обыкновенных дифференциальных уравнений и их решений рассмотрена в разделе, посвященном изучению автономных систем.
Опишем алгоритм решения задачи Коши для уравнения второго порядка y'' + a1 y' + a2 y = f(x), y(x0)=y0, (y)'(x0)=y0,1.
Будем искать решение задачи в виде y(x)= c1(x) y1(x) + c2(x) y2(x),
где y1(x), y2(x) — линейно независимые решения однородного уравнения y'' + a1 y' + a2 y = 0.
Вычислим y'(x), y''(x) и подставим полученные выражения в уравнение. Вычислим первую производную
y'(x)= (c1'(x) y1(x) + c2(x)' y2(x)) + (c1(x) y1'(x) + c2(x) y2'(x)), положим c1'(x) y1(x) + c2(x)' y2(x) = 0
и тогда y'(x)= c1(x) y1'(x) + c2(x) y2'(x), y''(x)= (y'(x))'= (c1(x) y1'(x) + c2(x) y2'(x))'=
=c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x).
Подставив y(x) и ее производные в уравнение, получим: y'' + a1 y' + a2 y =
=c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x) +
+a1(c1(x) y1'(x)+c2(x) y2'(x)) + a2(c1(x) y1(x)+c2(x) y2(x)) =
=c1(x)( y1''(x)+a1 y1'(x)+a2 y1(x)) + c2(x)( y2''(x)+a1 y2'(x)+a2 y2(x)) +
+c1'(x) y1'(x) + c2(x)' y2'(x) = 0 + 0 + c1'(x) y1'(x) + c2(x)' y2'(x) = f(x), при условии c1'(x) y1(x) + c2(x)' y2(x) = 0.
Тогда неизвестные функции c1(x) и c2(x) являются решениями системы линейных дифференциальных уравнений c1'(x) y1'(x) + c2(x)' y2'(x) = f(x),
c1'(x) y1(x) + c2(x)' y2(x) = 0
с известными y1(x) и y2(x).
Эта система легко разрешима относительно c1(x) и c2(x):
87
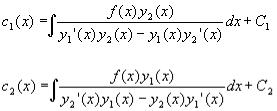
c1'(x) = f(x)y2(x)/(y1'(x)y2(x)-y1(x)y2'(x)), c1'(x)= f(x)y1(x)/(y1(x)y2'(x)-y1'(x)y2(x)).
Вычислив интегралы в правой части системы, получим
Произвольные константы C1 и C2 определяются из начальных условий.
ПРИМЕР 1. Решение методом вариации задачи Коши для линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами.
Заметим, что разрешимость системы дифференциальных уравнений для
c1'(x) и c2'(x) и однозначная разрешимость системы начальных условий для произвольных констант C1 и C2 гарантированы линейной независимостью y1(x) и y2(x), (y1'(x)y2(x)-y1(x)y2'(x))№0 для линейно независимых y1(x) и y2(x).
Для того чтобы решить задачу Коши для уравнения более высокого порядка действуем аналогично.
Решение задачи Коши ищем в виде
y(x)= c1(x) y1(x) + c2(x) y2(x) + ... + cn(x) yn(x),
где y1(x), y2(x), ..., yn(x) — линейно независимые решения соответствующего однородного уравнения.
Неизвестные функции c1(x) , c2(x), ..., cn(x)
находим как решения линейной системы дифференциальных уравнений c1'(x) y1(x) + c2(x)' y2(x) + ... + cn'(x) yn(x) = 0
c1'(x) y1'(x) + c2'(x) y2'(x) + ... + cn'(x) yn'(x) = 0, c1'(x) y1''(x) + c2'(x) y2''(x) + ... + cn'(x) yn''(x) = 0,
.................
c1'(x) y1(n-1)(x) + c2'(x) y2(n-1)(x) + ... + cn'(x) yn(n-1)(x) = f(x),
которая в силу линейной независимости y1(x), y2(x), ..., yn(x) разрешима относительно ci'(x). Вычислив ci(x) = Fi(x) + Ci находим произвольные постоянные Ci из начальных условий и тогда искомое решение уравнения имеет вид
y(x)= F1(x) y1(x) + F2(x) y2(x) + ...+ Fn(x) yn(x) + C1y1(x) + C2 y2(x) +...+ Cnyn(x).
Решение методом вариации произвольных постоянных задачи Коши для линейного неоднородного дифференциального уравнения 3-го порядка с постоянными коэффициентами.
Таким образом, для того чтобы решить методом вариации произвольных постоянных решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения l1, l2, ... , ln; найти фундаментальную систему решений y1(x), y2(x), ..., yn(x));
представить искомое решение задачи Коши в виде линейной комбинации
88

y(x)= c1(x)y1(x) + c2(x)y2(x) + ... + cn(x)yn(x),
с неизвестными функциями c1(x), c2(x), ..., cn(x); составить и решить систему для c1 (x), c2(x), ..., cn(x);
подставить вычисленные ci(x) = Fi(x) + Ci в выражение для решения и записать для него начальные условия;
найти из начальных условий значения констант Ci и записать искомое решение.
Решение методом вариации произвольных постоянных задачи Коши для линейного неоднородного дифференциального уравнения 4-го порядка с постоянными коэффициентами.
Для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения l1, l2, ... , ln, записать фундаментальную систему решений y1(x), y2(x), ..., yn(x));
найти методом вариации произвольных постоянных любое частное решение неоднородного уравнения yч(x);
записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x).
Доказательство формулы Лиувилля-Остроградского для линейной системы обыкновенных дифференциальных уравнений
Пусть вектор-функции 
















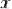
 — решения линейной системы ОДУ. Введем матрицу
— решения линейной системы ОДУ. Введем матрицу  следующим образом
следующим образом
Тогда 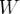








 . Воспользуемся тем, что
. Воспользуемся тем, что 


 - решения системы ОДУ, то есть
- решения системы ОДУ, то есть 











 .
.
В матричном виде последнее представимо в виде
или вводя производную от матрицы как матрицу из производных каждого элемента
Пусть 


 -
-  -я строка матрицы
-я строка матрицы 


 . Тогда
. Тогда
Последнее означает, что производная от  -й строки матрицы
-й строки матрицы 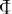


 есть линейная комбинация всех строк этой матрицы с коэффициентами из
есть линейная комбинация всех строк этой матрицы с коэффициентами из  -й строки матрицы
-й строки матрицы 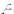


 .
.
89
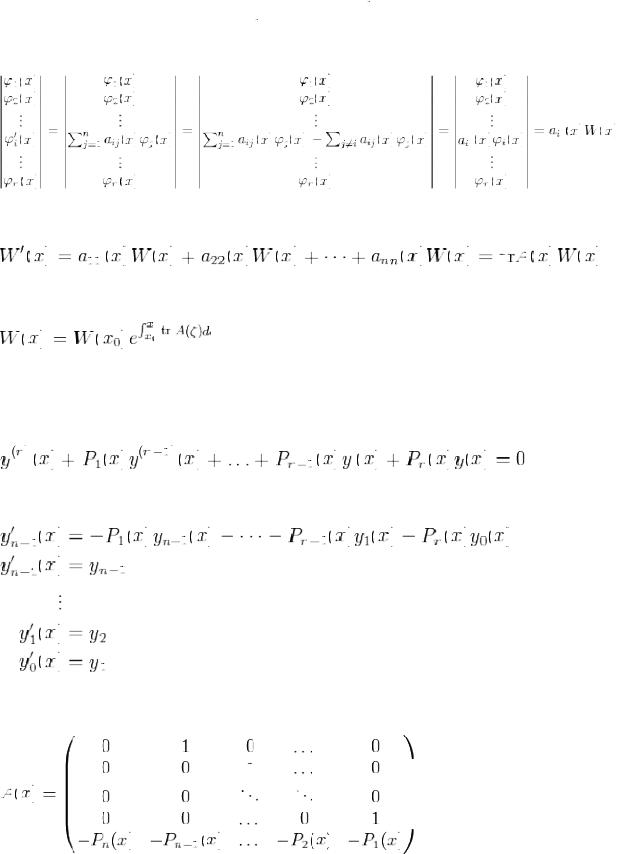
Рассмотрим определитель матрицы 


 , в которой
, в которой  -я строка продифференцирована. Определитель не изменится, если из
-я строка продифференцирована. Определитель не изменится, если из  -й строки этой матрицы вычесть линейную комбинацию всех остальных строк.
-й строки этой матрицы вычесть линейную комбинацию всех остальных строк.
Пользуясь формулой дифференцирования определителя, получаем
Последнее обыкновенное дифференциальное уравнение имеет решение
Доказательство для линейного дифференциального уравнения произвольного порядка
Линейное дифференциальное уравнение 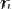 -го порядка
-го порядка
эквивалентно следующей системе
с матрицей 


 следующего вида
следующего вида
Вронскианы исходного уравнения и системы совпадают, а след матрицы 


 равен
равен




 . Подстановкой в формулу для системы получаем
. Подстановкой в формулу для системы получаем
90
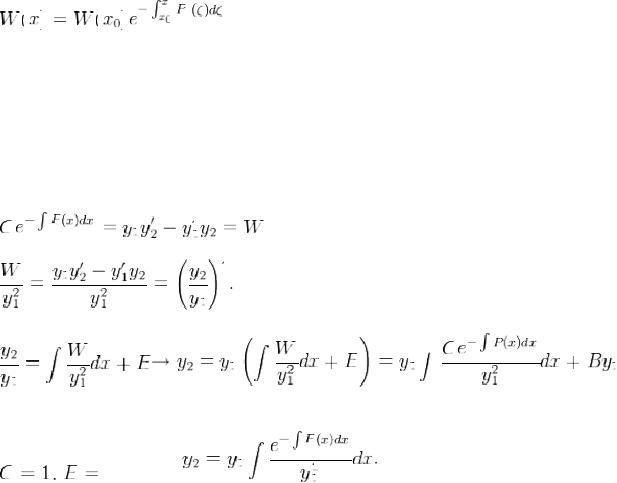
Применение формулы Лиувилля-Остроградского
Пусть известно решение 



 линейного обыкновенного дифференциального уравнения второго порядка. Используя формулу Лиувилля-Остроградского возможно найти линейно
линейного обыкновенного дифференциального уравнения второго порядка. Используя формулу Лиувилля-Остроградского возможно найти линейно
независимое от него решение 


 той же системы.
той же системы.
Распишем вронскиан:
поэтому
Так как для линейной независимости 



 и
и 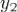


 достаточно
достаточно 

 , приняв
, приняв

 получим
получим
91
