Теоремы Ляпунова об устойчивости линейной системы

Полученное выше условие устойчивости справедливо для обыкновенных линейных систем автоматического управления. На практике приходится иметь дело с линеаризованными системами, и фактическая нелинейность характеристик системы может привести к неверным выводам о её устойчивости на основании исследования линеаризованного дифференциального уравнения.

Границы применимости линеаризованных дифференциальных уравнений при исследовании устойчивости систем определяются общими теоремами устойчивости А.М. Ляпунова. Эти теоремы приводятся ниже без доказательств. С доказательством теорем можно ознакомиться в учебниках по теории управления или в трудах А.М. Ляпунова.

1. Реальная система устойчива «в малом», если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями.

2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то реальная система будет неустойчива.

3. При наличии корней характеристического уравнения с нулевой вещественной частью поведение реальной системы может не совпадать с поведением линеаризованной системы, и решение вопроса об устойчивости системы требует дополнительных исследований.

Понятие "в малом" соответствует поведению системы при небольших начальных возмущениях, когда нелинейные зависимости между сигналами в системе не оказывают существенного влияния на её поведение.

Критерии устойчивости системы Общие сведения

Признаки, по которым можно судить об устойчивости системы автоматического управления без нахождения корней характеристического уравнения, в совокупности с правилами применения этих признаков, называются критериями устойчивости системы автоматического управления. Поскольку устойчивость системы определяется знаком вещественной части корней характеристического уравнения системы, то критерии устойчивости позволяют определить этот знак без нахождения самих корней.

Применение критериев устойчивости упрощает задачу исследования устойчивости системы, а также позволяет выявить причину её неустойчивости и наметить пути для устранения неустойчивости системы (для приведения системы к устойчивости).

Все критерии устойчивости делятся на алгебраические критерии, основанные на исследовании коэффициентов характеристического уравнения, ичастотные критерии, основанные на исследовании амплитудно-фазовых частотных характеристик системы.

В настоящее время известны алгебраические критерии А.И. Вышнеградского, Рауса и Гурвица. Критерий Вышнеградского и так называемая диаграмма Вышнеградского справедливы для систем регулирования, описываемых линейным дифференциальным уравнением третьего порядка. Критерий Рауса представляет собой алгоритм исследования коэффициентов характеристического уравнения. Наиболее распространен и удобен алгебраический критерий Гурвица. Критерии Рауса и Гурвица применимы для дифференциальных уравнений любого порядка.

Из частотных критериев получили распространение критерии А.В. Михайлова и Найквиста.

Критерии устойчивости Гурвица

Критерий Гурвица использует для оценки выполнения условия устойчивости системы коэффициенты характеристического уравнения замкнутой системы. Следовательно, для применения критерия Гурвица необходим характеристический полином замкнутой системы

.

Первым условием устойчивости системы автоматического управления по Гурвицу является положительность всех коэффициентов c_iхарактеристического уравнения. Если это условие не соблюдается, то система неустойчива. Для заключения об устойчивости системы условия положительности коэффициентов недостаточно.

Вторым условием устойчивости системы по Гурвицу является положительность всех определителей, составленных из коэффициентов характеристического полинома на основе таблицы Гурвица. Для уравненияn-порядка таблица Гурвица имеет следующий вид:

C1	C3	C5	C7	C9		0	0
C0	C2	C4	C6	C8		0	0
0	C1	C3	C5	C7		0	0
0	C0	C2	C4	C6		0	0
0	0	C1	C3	C5		0	0
0	…	…	…	…	….	0	0
0	…	…	…	…	….	Cn	0
0					….	Cn-1	0
0	0	0	0	0	….	Cn-2	Cn

При составлении таблицы по ее главной диагонали выписываются все коэффициенты характеристического уравнения, начиная с c₁поc_n. Затем каждый столбец таблицы, начиная с главной диагонали, дополняется коэффициентами: вверх – с возрастающим номером, вниз – с убывающим номером. Вместо отсутствующих коэффициентов ставятся нули. В результате получается таблица (матрица), содержащая нули и коэффициенты характеристического полинома замкнутой системы.

На основе таблицы составляются определители

;…

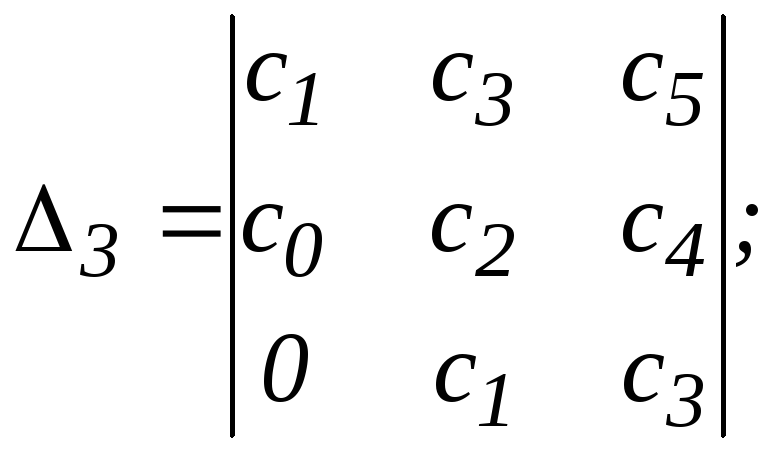Критерий Гурвица сводится к требованию положительности всех n определителей, составленных на основе таблицы, т.е. должно быть

,,….

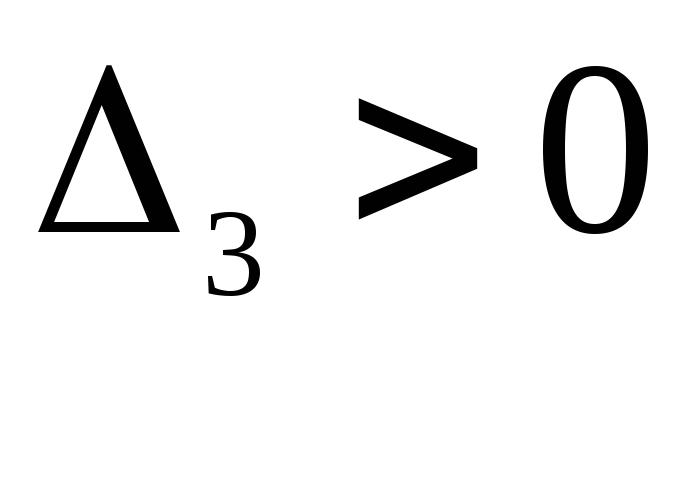Условием нахождения системы на границе устойчивости является равенство нулю последнего определителя

или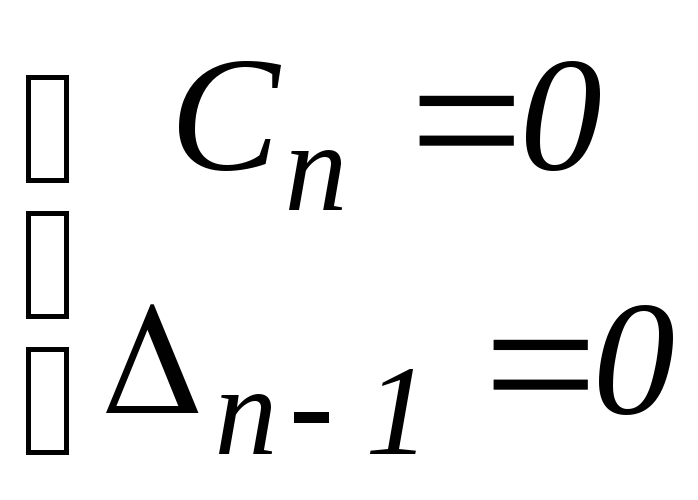

определяет границу устойчивости апериодического типа,– границу устойчивости колебательного типа.

Например, для системы третьего порядка характеристический полином

.

Т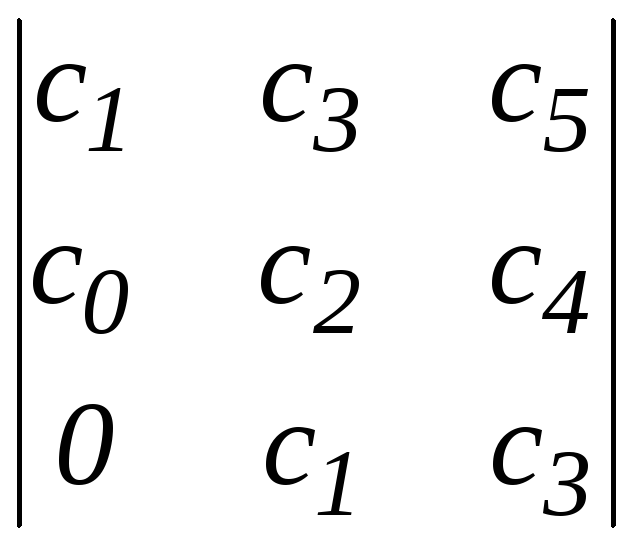аблица Гурвица для этого случая будет иметь следующий вид:

Для устойчивости системы необходимо выполнение требований ;;;, а также

При исследовании устойчивости по Гурвицу достаточно рассмотреть знак главных определителей, которые определяют знак всех остальных (зависимых) определителей. В литературе по теории управления на основе раскрытия определителей приводятся конечные условия устойчивости для систем разного порядка и нет необходимости каждый раз составлять таблицу Гурвица.