Преобразования структурных схем

При рассмотрении структурной схемы системы не всегда в её составе удаётся выделить в чистом виде одно из рассмотренных выше соединений. В этом случае возникает необходимость преобразования структурной схемы к такому виду, чтобы её можно было бы представить типовыми соединениями звеньев. Естественно, что при таком преобразовании сигналы в преобразованной структуре не должны измениться.

Преобразование структурных схем сводится либо к переносу точки соединения двух звеньев, либо к переносу внешнего воздействия (сумматора, к которому подводится внешнее воздействие). Для сохранения адекватности преобразованной схемы необходимо выполнять при преобразовании следующие правила.

1. Внешнее воздействие можно перенести со входа звена на его выход, добавив между воздействием и точкой приложения фиктивное звено с передаточной функцией исходного звена.

П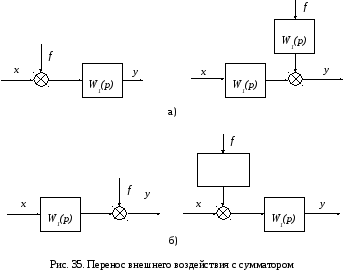ример показан на рис. 35а. Внешнее воздействиеf вместе с сумматором переносится со входа звенана выход этого звена. Чтобы сигналы в преобразованной схеме не изменились, при преобразовании добавляется фиктивное звено с передаточной функцией. Слева на рис. 35 показана исходная структура, справа – преобразованная.

Для исходной структуры , для преобразованной −, т.е. с точки зрения выходного сигнала обе схемы адекватны.

2. Внешнее воздействие можно перенести с выхода звена на его вход, добавив между воздействием и новой точкой его приложения фиктивное звено с передаточной функцией, обратной передаточной функции и исходного звена.

На рис. 35б внешнее воздействие fвместе с сумматором переносится с выхода звена(левая структурная схема) на его вход (правая схема). Для обеспечения адекватности преобразованной схемы в её структуру добавлено фиктивное звено с передаточной функцией. Легко убедиться в одинаковости выходной величиныв обеих схемах.

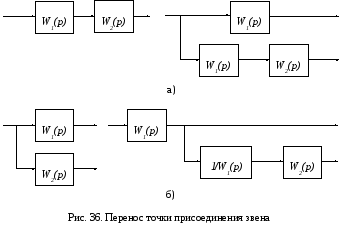3. Точку присоединения звена 2 можно перенести с выхода звена 1 на его вход, добавив между новой точкой присоединения звена 2 и входом звена фиктивное звено с передаточной функцией.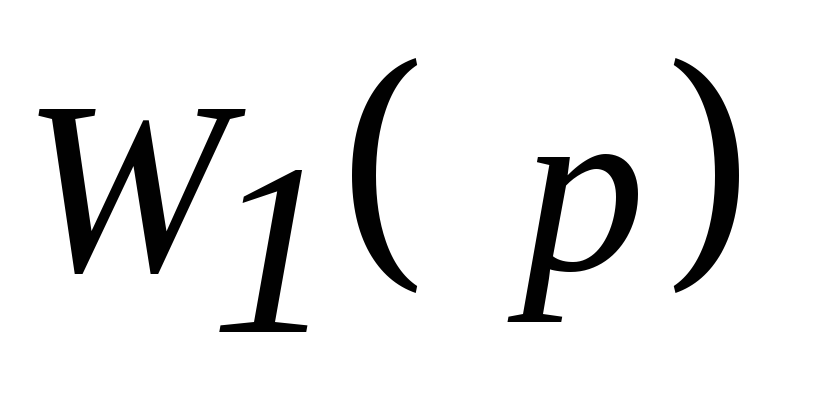

На рис. 36а звено присоединено к выходу звена(левая схема). Точка присоединения звенапереносится на вход звена(правая схема). Для сохранения сигналов в преобразованную схему добавлено фиктивное звено.

4. Точку присоединения звена 2 можно перенести со входа звена 1 на его выход, добавив между новой точкой присоединения звена 2 и его входом фиктивное звено с передаточной функцией, обратной передаточной функции первого звена.

Это правило поясняется рис. 35б. В исходной структуре звено присоединено ко входу звена. В преобразованной структуре точка присоединения перенесена на выход звена. Добавление фиктивного звена позволяет сохранить сигналы в системе неизменными.

Передаточная функция замкнутой системы автоматического управления

В

y(t)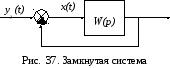

системах автоматического управления наиболее распространён принцип управления по отклонению (по ошибке). Структурную схему системы автоматического регулирования с управлением по отклонению можно представить в виде, показанном на рис. 37. Структура замкнутой системы включает глобальную единичную обратную связь с выхода системы на её вход. Наличие глобальной обратной связи обеспечивает реализацию управления по ошибке, когда устройство управления постоянно сравнивает фактическое значение выходной управляемой величины с её заданным значением и вырабатывает управляющее воздействие таким образом, чтобы устранить возникающую ошибку.

Свойства замкнутой системы автоматического управления описывает передаточная функция замкнутой системы

.

Для структуры на рис. 37 общая передаточная функция может быть найдена с использованием правила нахождения передаточной функции соединения звеньев с обратной связью

,

где W(p) –передаточная функция разомкнутой системы.

Передаточная функция замкнутой системы иногда называется в литературе главным оператором системы. Передаточная функция замкнутой системы в общем случае является дробной функцией вида

.

Поскольку передаточная функция W(p)разомкнутой системы является дробью

, то,.

Полином C(p), стоящий в знаменателе выражения передаточной функции замкнутой системы, называетсяхарактеристическим полиномом замкнутой системы. Приравнивание нулю характеристического полинома даётхарактеристическое уравнение замкнутой системы

.

Характеристическое уравнение замкнутой системы является алгебраическим уравнением степени n и имеет в общем случаеn корней. Эти корни являютсяполюсами передаточной функциизамкнутой системы. Решение уравнения, полученного приравниванием нулю полинома, стоящего в числителе передаточной функции,

дает нули передаточной функциизамкнутой системы автоматического управления.

Подстановкой из передаточной функции замкнутой системы можно получить частотную передаточную функцию замкнутой системы

.
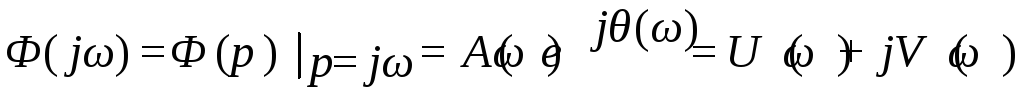