Частотная передаточная функция системы автоматического управления

Частотные характеристики системы автоматического управления определяются при подаче на вход системы гармонического воздействия:

,

где (формула Эйлера).

При подаче такого сигнала на вход и после затухания переходных процессов на выходе установятся также гармонические колебания с той же частотой , но с другой амплитудой и фазой (рис. 19). Тогда для выходного сигнала можно записать

y(t) = y_m=y_m,

где – угол фазового сдвига выходного сигнала относительно входного;– период сигнала;– круговая частота сигнала.

Пусть исследуемая линейная система описывается обыкновенным линейным дифференциальным уравнением

При гармоническом входном сигнале можно в этом уравнении определить все производные входной величины:

,

,

....................................................................................

.

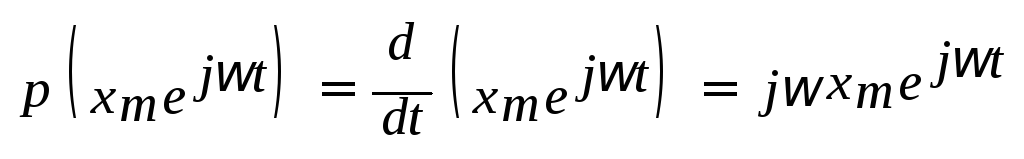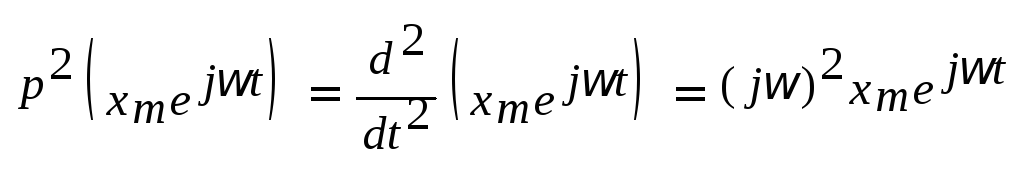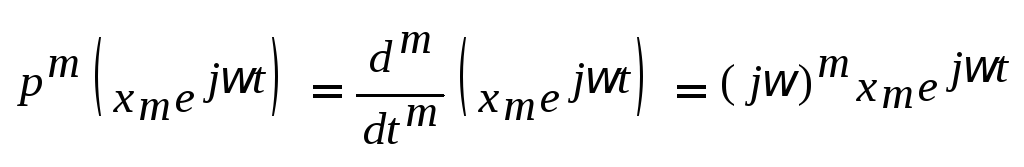Аналогично определятся и производные выходной величины. В результате исходное дифференциальное уравнение можно переписать в виде алгебраического уравнения

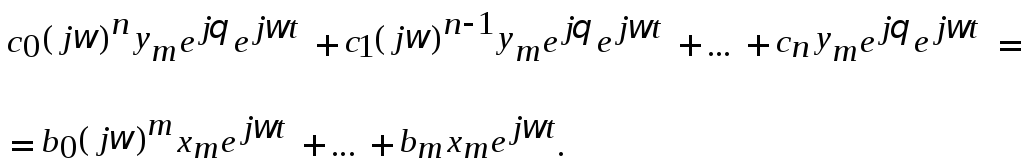
Решив это уравнение, получим

^.

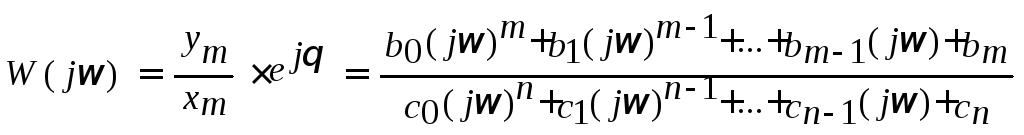Величина W(j)называетсякомплексной частотной функцией (или частотной передаточной функцией). Комплексная частотная функция может быть найдена по передаточной функции путем подстановкиp = j:

Частотная передаточная функция является комплексным выражением

где A()– модуль частотной передаточной функции;θ() – фазовый угол (аргумент); – вещественная составляющая передаточной функции;V() = JmW(j)– мнимая составляющая частотной передаточной функции.

Для частотной передаточной функции справедливы следующие соотношения:

,.

Зависимости А () и () определяют изменение амплитуды и фазы колебаний на выходе системы при изменении частотывходных колебаний. Модуль частотной характеристикиA () определяет коэффициент усиления системы для гармонического сигнала с частотой.

Частотные характеристики системы автоматического управления

Частотную передаточную функцию W(j), являющуюся комплексным выражением, можно представить в векторной форме. При изменении частоты входного сигнала в пределах –<< +конец вектора опишет годограф, который называютамплитудно-фазовой частотной характеристикой(АФЧХ) (рис. 20).

А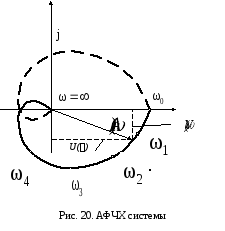ФЧХ строится по точкам. Отрицательная ветвь характеристики АФЧХ при(на рис. 20 показана пунктиром) зеркально ото-бражает положительную ветвь. Поэтому при аннализе системы достаточно построить положитель-ную ветвь АФЧХ при изменении частоты.

Амплитудно-фазовая час-тотная характеристика широко применяется при исследовании систем автоматического управления, например при исследовании устойчивости системы автоматического управления.

Наряду с АФЧХ частотные свойства системы описываются также логарифмическими частотными характеристиками (ЛХ):логарифмическая амплитудно-частотная характеристика(ЛАХ) илогарифмическая фазовая частотная характеристика(ЛФХ). Логарифмическая амплитудно-частотная характеристика обычно обозначается какL()и находится из соотношениядБ. Величинавыражается в децибелах.

Логарифмическая амплитудная частотная характеристика ЛАХ строится в координатах –, при этом для осииспользуется логарифмический масштаб. Использование логарифмического масштаба для оси частот приводит к тому, что эта ось разбивается на одинаковые участки –декады, в пределах которых частота увеличивается в 10 раз.

Логарифмическая фазовая характеристика ЛФХстроится в координатах–. Координатные сетки обеих характеристик объединяются и представляются в общепринятой форме, показанной на рис. 21.

Особенностью построений на рис. 21 является то, что положительное направление оси θ() выбирается вниз – противоположно общепринятому направлению.

По оси абсцисс оцифровка ведется в единицах частоты , сами величины откладываются в логарифмическом масштабе. Частотный интервал, соответствующий удвоению частоты, называетсяоктавой. Частотный интервал, соответствующий изменению частоты в 10 раз, называетсядекадой.

Достоинством логарифмических характеристик является их более простое построение, по сравнению с АФЧХ, а также возможность получения суммарной характеристики для соединения элементов простым суммированием ЛАХ и ЛФХ элементов.

Л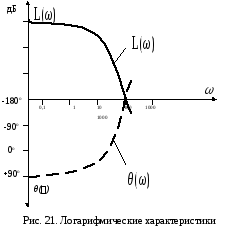огарифмическая амплитудно-частотная характеристика строго может быть построена в том случае, когда передаточная функция не имеет размерности. Поэтому при построении логарифмических характеристик системы передаточную функ-цию системы следует преобразовать к такому виду, когда коэффициент преобразования системы становится безразмерным.

Частотные характеристики системы используются при исследовании устойчивости и качества системы автоматического управления.