Posob_2012_Ok

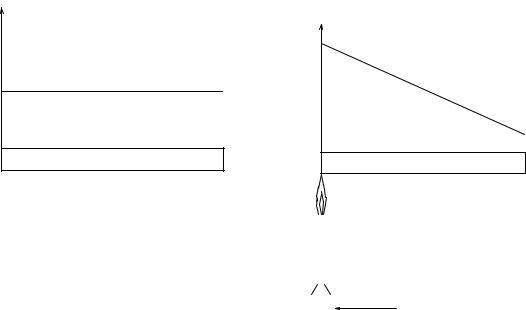
ется такое состояние системы, которое не изменяется во времени, причем эта неизменность не поддерживается каким либо внешним по отношению к системе процессом (см. рис. 2.1). При равновесном состоянии системы температура и давление во всех ее частях остаются одинаковыми.

Впростых системах состояние равновесия может определяться Р, Т,

вболее сложных (например, растворы) - еще и концентрациями слагающих систему веществ.

Все эти величины, определяющие состояние системы (неравновесное, стационарное, равновесное), называются параметрами состояния.

Равновесное состояние теперь можно определить как состояние, определяющееся конечным числом остающихся постоянными во времени параметров, с условием, если это постоянство не поддерживается внешним по отношению к данной системе процессом.

Равновесное состояние в системе нередко устанавливается в результате уравновешивания скоростей противоположных процессов, такое равновесие носит название динамического. Например, L+S (жидкое и твердое) при температуре плавления или L+V (жидкое и парообразное) при температуре кипения.

Рис. 2.1. Примеры равновесного (а) и стационарного (б) процессов.

Определим теперь понятия равновесных и обратимых процессов. Равновесным, или квазистатическим, процессом называется непрерывная последовательность равновесных состояний, характеризующихся тем, что система, пройдя ее, выполняет наибольшую работу, которую она способна произвести, проходя данный непрерывный ряд состояний. Для того чтобы получить эту работу, необходим соответствующий аппарат; без него это

21

количество энергии, эквивалентное работе, выделится в виде теплоты.

В равновесных процессах система при прямом и при обратном процессе проходит через одни и те же состояния.

Под обратимым подразумевается процесс, для которого начальное и конечное состояния таковы, что возможен процесс, имеющий своим единственным результатом возвращение системы из конечного состояния в начальное. Условием обратимости процесса является равновесность всех его слагающих частных процессов.

2.2. Понятие о компонентах и фазах. Гетерогенные равновесия Компоненты - индивидуальные химические вещества, которые, бу-

дучи взятыми в наименьшем числе, достаточны для построения всей системы, находящейся в состоянии равновесия.

Другое определение: компоненты - независимые составные части системы, например: СаО + СО2 = СаСО3. В этом случае для образования всей системы достаточно двух веществ: СаО и СО2, СО2 и СаСО3, СаО и

СаСО3.

Если в системе химические реакции не могут идти, то число компонентов равно числу составных частей, причем под составными частями системы подразумеваются те образующие ее вещества, которые способны к существованию в изолированном виде, такая система называется физической или системой первого класса.

Если в системе протекают химические реакции, то число компонентов равно числу составных частей, уменьшенному на число независимых химических реакций, которые идут в ней; такая система называется химической или системой второго класса.

Фазой называется совокупность всех гомогенных частей системы, одинаковых во всех точках по составу и по всем химическим и физическим свойствам и отграниченных от других частей некоторой поверхностью раздела, на которой скачкообразно изменяются все эти признаки.

Другими словами, фаза - это гомогенная часть гетерогенной системы, находящейся в термодинамическом равновесии.

Приведем примеры фаз. Если вода находится в равновесии с паром, то в этой системе имеются две фазы: вода и пар. В системе, состоящей из насыщенного раствора соли, кристаллов соли и пара, имеются три фазы. Право- и левовращающие кристаллы NаСlО3 мы считаем одной фазой, так как их термодинамические свойства одинаковы. Различия в их оптических свойствах зависят исключительно от строения кристаллов. Наоборот, право- и левовращающие кристаллы винной кислоты мы относим к разным фазам, так как вращательная способность является свойством самой молекулы, т. е. оптические изомеры винной кислоты - это различные вещества

(Н6С4О6).

Равенства давления, температуры и химических потенциалов каж-

22

дого компонента во всех фазах представляют собой условия равновесия в гетерогенной системе.

2.3. Термодинамические и химические потенциалы и их применение в учении о равновесии

Для изолированных систем энтропия (S) является удобным параметром для оценки самопроизвольного протекания процессов, а также достижения равновесия. В качестве такового выступает величина dS или ∆S. Увеличение энтропии системы представляет собой критерий самопроизвольного протекания процесса: dS > 0. В момент достижения равновесия:

системы.

Если же системы не изолированы, то этот критерий оценки самопроизвольного протекания процессов и достижения равновесия становится неприемлемым. С другой стороны, на практике постоянно приходится встречаться именно с таким случаем, когда, например, при изотермическом проведении процесса постоянство температуры обеспечивается теплообменом со средой (термостатом). Значит, в данном случае нужно использовать другой критерий.

2.3.1. Энергия Гельмгольца (свободная энергия, изохорно-изотермический потенциал)

По первому началу термодинамики δQ = dU + δА. Если вместо δQ подставить величину ТdS, учитывая как обратимые, так и необратимые

Видно, что работа системы при постоянной температуре равна или меньше убыли функции F за время процесса. Зададимся вопросом: каков же физический смысл функции F?

Согласно предыдущему, U = F + ТS. Сравнивая это выражение с (2.2), можно отметить, что при постоянной температуре в работу может перейти не вся внутренняя энергия, а только та ее часть, которую мы обо-

23

значили буквой F. Эта часть энергии названа свободной энергией системы (энергия Гельмгольца, изохорно-изотермический потенциал, изохорный потенциал).

Таким образом, свободной энергией называется та часть внутренней энергии системы, которая может быть превращена в работу при постоянной температуре; эта работа максимальна, т. е. равна падению свободной энергии системы, если процесс обратим; при необратимых процессах часть свободной энергии теряется непроизводительно (трение, лучеиспускание и т.п.) и работа меньше максимально возможной.

Та часть внутренней энергии, которая при постоянной температуре не превращается в работу (ТS), называется связанной энергией. Обозначим

еечерез К:

К= ТS; dК = ТdS + SdТ; dТ = 0, поэтому dК = ТdS = δQ и ∆К = Т∆S

=Q.

Итак, связанная энергия при изменении системы при Т= const не дает работы, а переходит только в теплоту, она - изотермически бесполезная часть внутренней энергии. К = ТS. Видно, что энтропия является фактором емкости связанной энергии, а этот фактор обладает свойством аддитивности.

Покажем, что свободная энергия - это сложная функция несколь-

ких переменных. F = U - ТS; dF = dU - ТdS - SdТ; так как dU = ТdS - δА

(для обратимых процессов), то получаем: dF = -δА - SdТ. Когда совершает-

т. е. давление есть мера убыли свободной энергии с ростом объема при постоянной температуре; энтропия есть мера убыли свободной энергии системы с ростом температуры при постоянном объеме.

Вернемся несколько назад: dF =dU - ТdS - SdТ; рассматривая как

Рассмотрим уравнение (2.6). Полагая Т = const и V = const, а также при условии отсутствия всех других видов работы, получаем (∂F)V, T ≤ 0, т.е. изохорный потенциал системы, находящейся при постоянных V и T, не изменяется при равновесных (обратимых) процессах и убывает при неравновесных (необратимых) процессах.

24

Таким образом, мы получили новый критерий оценки направления течения процесса и критерий равновесия при T = const и V = const.

Условия, которым должны удовлетворять процессы, для того чтобы по изменениям величины F можно было судить о направлении этих процессов, иные, чем для энтропии. Для энтропии это были условия постоянства внутренней энергии и объема (условия изолированной системы), для изохорного потенциала - это условие постоянства объема и температуры - легко измеряемых параметров системы. Изохорный потенциал, являясь производным понятием по отношению к энтропии, представляет собой практически более удобный критерий направления процессов, чем энтропия.

2.3.2. Энергия Гиббса (свободная энтальпия, изобарно-изотермический потенциал, свободная энергия при постоянном давлении)

Рассмотрим теперь случай, когда в системе происходят одновременно две работы, например в гальваническом элементе - электрическая работа и работа расширения. Первая работа полезная, вторая - нет, но она неизбежна в случае постоянства давления.

Для такого случая мы можем записать первый закон термодинамики в виде: δQ = dU+pdV+δА', откуда δА' = δQ - dU - pdV, и после подстановки

При использовании формулы δА ≤ ТdS-dU мы налагали на нее только одно условие - постоянство температуры, а поэтому в выражении А ≤ F1 - F2 работа А могла быть и при постоянном объеме и при постоянном давлении. При дальнейшем же использовании формулы (2.7) мы сразу налагаем на нее два условия - постоянство температуры и постоянство давления, и тогда после интегрирования (2.7) получим: А' ≤ Т(S2-S1) ' - (U2 -U1) - p(V2 -V1), или А' ≤ (U1 - ТS1 + pV1)-(U2 - ТS2 + pV2).

откуда, в частности, следует, что G = F +pV и G = H -TS, тогда получим: А'≤G1-G2, или А' ≤ - ∆G, если процесс протекает при постоянных давлении и температуре.

Величина G есть новая функция состояния системы; она носит название энергии Гиббса (изобарно-изотермического потенциала, изобарного потенциала, свободной энергии при постоянном давлении). Работа А′ называется полезной работой, в ее состав не входит работа изменения объе-

25

ма. Она является полезной максимальной работой в случае обратимых

процессов, когда А' = -∆G; при необратимых процессах эта работа А' < -

∆G.

Для получения полного дифференциала функции G при переменных p и Т дифференцируем уравнение (2.8):

dG = dU - ТdS - SdТ + pdV + Vdp; dU ≤ТdS - pdV - δА'; dG ≤ -δА'- SdТ+Vdp.

При отсутствии всех видов работы, кроме работы расширения

увеличением давления при постоянной температуре, а энтропия есть мера убыли G с ростом температуры при постоянном давлении. Из уравнения dG ≤ Vdp - SdТ получаем при постоянных p и Т: (∂ G)P, T ≤ 0, т.е. изобарный потенциал системы при постоянных p и Т уменьшается при неравновесных (необратимых) процессах и остается постоянным при равновесных (обратимых) процессах. Очевидно, равновесное состояние системы при данных p и Т соответствует минимуму изобарного потенциала. Таким образом, условием равновесия системы при постоянных p и Т является:

(∂G) P, T < 0 - критерий самопроизвольного протекания процессов. Снова вернемся к формулам G = H - ТS и G = F + pV. Первая из них

показывает, что ∆G = ∆H - Т∆S, вторая же показывает, что ∆G = ∆F + p∆V,

или -∆G = -∆F - p∆V, что окончательно дает: A'max = Аmax- p∆V, т.е. полезная максимальная работа равна общей максимальной работе процесса

за вычетом работы изобарного расширения (p∆V). Изохорно-изотермический и изобарно-изотермический потенциалы

принадлежат к классу функций состояния системы, носящих название термодинамических потенциалов. Это величины, которые имеют размерность энергии и стремятся к минимуму, если процессы в системе протекают в определенных условиях. Термодинамические потенциалы являются в этих условиях критериями направления процесса; минимальные значения их при тех же условиях отвечают равновесию системы и являются условиями равновесия.

К термодинамическим потенциалам относятся также внутренняя

26

энергия U и энтальпия H системы. Как известно, ТdS ≥ dU +δА, отсюда

Видно, что U = U(S,V). Снова можно через частные производные выразить параметры состояния: (∂U/∂S)V = Т; (∂U/∂V)S = -p. При

постоянных S и V получим (∂U)S,V ≤ 0.

При всех неравновесных (необратимых) изохорно-изэнтропных процессах внутренняя энергия убывает, т.е.(∂U)S,V < 0 - критерий направления самопроизвольного протекания процессов. Когда величина U достигает минимума, система приходит в равновесие. Условия равновесия, очевидно, следующие:

Итак, U - это тоже термодинамический потенциал, это изохорноизэнтропный потенциал.

Для энтальпии также можно получить уравнение, аналогичное

(2.11): H=U+pV; dH = dU +pdV + Vdp;

dH ≤ ТdS + Vdp. (2.12)

Видно, что H = H(S,p). Через частные производные можно выразить некоторые параметры состояния системы: (∂H/∂S)P = Т; (∂H/∂P)S = V. При постоянных S и p уравнение (2.12) приобретает вид: (∂H )S, P ≤ 0. Итак, критерием направления процесса служит (∂H)S, P< 0. Условия равновесия, очевидно, следующие:

Итак, H - это тоже термодинамический потенциал, это изобарно-из- энтропный потенциал.

Эти функции U и H могут служить критериями равновесия при условии постоянства энтропии. Энтропию непосредственно измерить нельзя, и контроль ее постоянства при неравновесных (необратимых) процессах затруднен. Поэтому функции U и H не находят широкого применения в качестве критериев направления процесса и равновесия.

Напишем и сопоставим еще раз выражения для полных дифференциалов функций U, H, F и G:

dU = ТdS - pdV, dH = ТdS + Vdp, dF = -SdТ - pdV, dG = -SdТ + Vdp.

Эти выражения образуют замкнутую группу, в которой две пары переменных - Т и S (параметры, связанные с теплотой) и p и V (параметры, связанные с работой) - дают все возможные сочетания.

27

В зависимости от характера изучаемого процесса может быть использована та или иная функция.

Частными производными четырех функций при данном, характерном для каждой из них наборе независимых переменных являются основные параметры состояния системы: p, V, T и S. Отсюда вытекает важное свойство этих функций: через каждую из этих функций и ее производные можно выразить в явной форме любое термодинамическое свойство системы.

Каждая из функций U, H, F, G дает полную термодинамическую характеристику системы. Поэтому указанные функции (термодинамические потенциалы) называют характеристическими.

Характеристические функции (например, термодинамические потенциалы, а также энтропия) могут служить критериями направления процесса и равновесия:

На основании этого сопоставления можно сформулировать условия равновесия системы следующим образом: в состоянии равновесия системы термодинамические потенциалы ее имеют минимальное значение при постоянстве своих естественных переменных, а энтропия имеет максимальное значение при постоянстве внутренней энергии и объема системы.

Все сказанное справедливо для процессов, происходящих в системах, в которых исключены химические превращения, приводящие к изменению масс составных частей этих систем. Если же в системе возможны химические процессы, то следует еще учесть dU, dH, dF, dG, вызванное изменением этих масс.

Например, внутренняя энергия раствора изменяется при поглощении или выделении теплоты, совершении работы и при изменении масс компонентов, поэтому выражение первого начала термодинамики нужно

Здесь n1, n2,...ni - массы компонентов раствора, выраженные числом молей; µ1, µ2, ... µi - коэффициенты пропорциональности между dU и dni. Учитывая, что F=U-ТS, получим dF = dU - ТdS - SdТ. Если сюда вместо dU подставить его значение из (2.14), то dF = ТdS - pdV + Σµidni - ТdS - SdТ

Это выражение есть полный дифференциал функции F = F(V, Т, n1,

28

потенциала по массе i-го компонента при постоянстве объема и температуры системы и масс остальных компонентов (индекс \ni показывает, что масса i-го компонента исключается из ряда индексов неизменных масс).

Величины µi называются химическими потенциалами.

Выражение для полного дифференциала изобарного потенциала по-

Из этого снова заключаем, что µi является частной производной изобарного потенциала по массе i-го компонента при постоянстве давления, температуры и масс остальных компонентов.

Из определения µi как частной производной F и G вытекает следующее. Если при постоянной температуре к бесконечно большому количеству раствора определенного состава (т.е. с определенными концентрациями компонентов) добавить один моль какого-нибудь одного компонента, то химический потенциал будет равен приросту изобарного потенциала в том случае, когда p=const, или приросту изохорного потенциала в том случае, когда V=const.

Бесконечно большое количество раствора рассматривается здесь потому, что только в этом случае добавление в раствор одного моля компонента не изменит состава (концентраций компонентов) раствора.

Химический потенциал можно также выразить через частную производную внутренней энергии из уравнения (2.14):

жения для полного дифференциала энтальпии: H = U + pV; dH = dU + pdV + Vdp;

ni.

Таким образом, химический потенциал компонента раствора данного состава при данных p и Т имеет определенное числовое значение, хотя и неизвестное по абсолютной величине.

Все рассмотренные уравнения применимы ко всей системе в целом

Функция G = G(n1, n2,...ni) обладает интересным свойством: если массы всех компонентов системы возрастают в одно и то же число раз, то и изобарный потенциал системы возрастает в то же число раз. На самом деле, увеличение массы всех компонентов раствора (при постоянных p и Т), например, в 2 раза идентично увеличению массы всего раствора в 2 раза без изменения его состава. Очевидно, величина G = U - ТS + pV возрастает также в 2 раза (ибо U, S, V возрастают пропорционально массе).

Таким образом, интегрируя уравнение (2.22) при постоянных отно-

При указанных условиях величины µi остаются постоянными в процессе нарастания массы, т.е. (при постоянных p и Т) они зависят только от состава раствора, а не от абсолютных масс компонентов и являются факторами интенсивности.

Изложенное позволяет определить химический потенциал компонента как изобарный потенциал системы (или фазы), приходящийся на один моль компонента.

Продифференцируем уравнение (2.23):

dG = n1dµ1 + n2dµ2 + ....+ nidµi + µ1dn1 + µ2dn2 +....+ µidni = Σnidµi +

Σµidni Правые части этого уравнения и уравнения (2.22) равны, поэтому

(при p = const, Т = const):

Уравнения (2.24) и (2.25) называются уравнениями Гиббса-Дюгема. Они имеют большое значение в термодинамике растворов.

Сейчас нужно вывести соотношение между химическими потенциалами компонента, входящего в состав нескольких фаз гетерогенной системы.

Переход массы dni компонента из одной фазы (′) в другую (′′) при равновесии и постоянных давлении и температуре обусловливает изменение изобарного потенциала dG системы, которое складывается из измене-

ний изобарных потенциалов dG′ и dG′′ обеих фаз: dG = dG′′ + +dG′ =

µi′′dni′′+ µi′dni′.

Так как dni′′= - dni′ и при условии равновесия dG = 0, то µi′′dni′′-

µi′dni′′ = 0, или (µi′′- µi′)dni′′= 0, или µi′′- µi′ = 0; µi′′ = µi′.

Данный вывод можно распространить на третью, четвертую и т.д. фазы. Таким образом, химические потенциалы данного компонента во всех фазах системы, находящейся в равновесии, равны между собой.

При отсутствии равновесия, очевидно, dG = (µi′′- µi′)dni′′ < 0. Отсюда следует, что если µi′′- µi′ > 0 (µi′′> µi′), то dni′′< 0, если же

30