Тема 2. Динамика материальной точки

1. Дифференциальные уравнения движения материальной точки

Используя основное уравнение динамики материальной точки (1.5), можно получить дифференциальные уравнения движения материальной точки в различных системах координат.

1.1. Дифференциальное уравнение движения материальной точки в векторной форме

Пусть материальная точка M массой движется под действием равнодействующей всех заданных сил и сил реакций связей (рис. 2), применяяуравнение динамики материальной точки (1.5), получим

, (2.1)

где - вектор ускорения точкиM.

Из кинематики точки известно, что ускорение движущейся точки и ее радиус-векторсвязаны соотношением

.

Подставляя это соотношение в формулу (2.1), получим

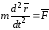.(2.2)

Формула (2.2) является дифференциальным уравнением движения материальной точки в векторной форме.

1.2. Дифференциальные уравнения движения материальной точки

в декартовой системе координат

Проецируя уравнение (2.1) на оси декартовой прямоугольной системы координат, получим

,,,

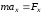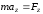где ,,- проекции ускорения точки на оси декартовых координат.

Из кинематики точки известны соотношения:

, ,,

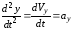йгде , ,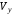-проекции скорости точки на оси декартовых координат.

Окончательно, получим

,

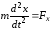, (2.3)

.

Полученная система уравнений (2.3) представляет собой дифференциальные уравнения движения материальной точки в декартовой системе координат.

1.3. Дифференциальные уравнения движения материальной точки

для естественных подвижных осей

Проецируя уравнение (2.1) на естественные подвижные оси координат (рис. 3), получим

; ;,

где ,,,,,– соответственно проекции векторов ускорения и равнодействующей силы на касательную, главную нормаль и бинормаль к траектории.

Из кинематики точки известны следующие соотношения:

; ;,

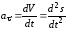где - радиус кривизны траектории,

- скорость материальной точки.

Подставляя эти соотношения в выражения для ,,, получим

;

; (2.4)

.

Полученные уравнения называют дифференциальными уравнениями движения материальной точки для естественных подвижных осей. Эти уравнения иногда удобны для исследования движения точки по плоским траекториям.

2. Две основные задачи динамики материальной точки

Используя дифференциальные уравнения движения материальной точки в векторной (2.2), координатной (2.3) или естественной (2.4) форме, можно решать две основные задачи динамики материальной точки. Рассмотрим эти задачи.

2.1. Первая основная задача динамики материальной точки

Первую основную задачу динамики материальной точки формулируют следующим образом: по заданной массе материальной точки и закону ее движения требуется определить действующую на эту точку силу.

Рассмотрим порядок решения этой задачи для случая, если движение материальной точки массой задано координатным способом.

1. Пусть координаты движущейся точки заданы как функции времени:

; ;.

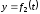2. Определяем проекции силы на координатные оси из дифференциальных уравнений движения (2.3) по формула

; ;.

3. Зная проекции силы на координатные оси, определяем модуль искомой силы, а также ее направляющие косинусы по формулам

,

; ;.