6.5.2.3. Кинетическая энергия твердого тела при его плоском движении

При плоском движении твёрдого тела кинетическую энергию определяют по теореме Кёнига. Рассмотрим применение этой теоремы для определения кинетической энергии твердого тела при его плоском движении.

Рассмотрим плоское движение твёрдого тела в плоскости Oxy (рис. 27).

Рис. 27. Плоское движение твердого тела

В качестве полюса выберем центр масс твёрдого тела точку С. Тогда по теореме сложения скоростей для произвольной точки твёрдого тела 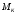при его плоском движении, получим

,

где - вектор скорости центра масс телаC,

- скорость точки в ее движении по отношению к центру масс C (движение носит вращательный характер).

Подставляя данное выражение в формулу (4.60), получим

.

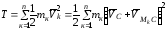Раскрывая скобки, получим

. (4.63)

Рассмотрим первое слагаемое выражения (4.63), которое характеризует движение центра масс:

.

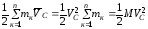Рассмотрим второе слагаемое выражения (4.63):

,

где - статический момент массы твердого тела относительно его центра масс.

Таким образом, получили, что второе слагаемое выражения (4.63) равно нулю:

.

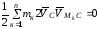Рассмотрим третье слагаемое выражения (4.63):

,

где - угловая скорость вращения тела,

- момент инерции тела относительно центральной оси проходящей через центр масс С и перпендикулярной плоскости Oxy.

Учитывая приведенные выражения, для кинетической энергии твёрдого тела, совершающего плоское движение, окончательно получим

. (4.64)

Таким образом, при плоском движении твёрдого тела кинетическая энергия складывается из кинетической энергии центра масс, считая что в нём сосредоточена вся масса тела и кинетической энергии вращательного движения твёрдого тела по отношению к центру масс.

6.6. Теорема об изменении кинетической энергии для точки

Рассмотрим движение материальной точки M массой m, движущуюся со скоростью , под действием силы.

Представим основной закон динамики материальной (2.1) точки в виде

.

Умножив обе части равенства скалярным образом на дифференциал радиус-вектора точкиM, получим

.

Рассмотрим правую и левую части этого равенства. Правая часть этого равенства представляет собой элементарную работу силы , выражаемую по формуле (4.31):

.

Для левой части получим

.

Таким образом, окончательно имеем

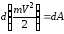. (4.65)

Формула (4.65) выражает теорему об изменении кинетической энергии материальной точки в дифференциальной форме, которую можно сформулировать следующим образом: дифференциал от кинетической энергии материальной точки равен элементарной работе силы, действующей на эту точку.

Разделив (4.65) на , получим

. (4.66)

Формула (4.66) выражает вторую формулировку теоремы об изменении кинетической энергии материальной точки в дифференциальной форме. Производная по времени от кинетической энергии материальной точки равна мощности силы, действующей на точку.

Интегрируя выражение (4.65) в соответствующих пределах, получим

, (4.67)

где - масса материальной точки,

- скорость точки в момент времени, когда она занимает положение ,

- скорость точки в начальный момент времени, когда она занимает положение ,

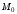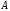- полная работа силы, действующей на точку при её перемещении из начального положения M₀ в конечное М, определяемая по формуле (4.36)

.

Формула (4.67) выражает теорему об изменении кинетической энергии в интегральной (конечной) форме, которая формулируется следующим образом: изменение кинетической энергии точки, на каком-либо её конечном перемещении равно полной работе силы, действующей на точку на этом же перемещении.