6. Теорема об изменении кинетической энергии

6.1. Элементарная работа силы

Рассмотрим материальную точку М массой m, движущуюся по произвольной траектории со скоростью , под действием силы (рис. 19).

Рис. 19. Движение материальной точки под действием силы

Введем понятие элементарной работы силы. Элементарной работой силы F на элементарном бесконечно малом перемещении dS называется произведение проекции этой силы на направление скорости на элементарное перемещение. Элементарную работу определяют по формуле

, (4.29)

где - проекция силына направление скорости точки ее приложения или на направление элементарного перемещения, которое считается направленным по вектору скорости точки.

Элементарная работа является скалярной величиной, и её знак определяется знаком проекции силы . Если> 0, то> 0, если< 0, то< 0.

Обозначим φ угол между вектором силы 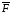и вектором скорости, тогда

Подставляя в выражение (4.29), получим

(4.30)

В формуле (4.30) величины F и dS положительны, поэтому если φ < 90⁰, то dA положительна, если 180<φ<90, то dA отрицательна.

Рассмотрим три частных случая:

1. Если , то;

2. Если , то;

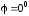3. Если , то.

Таким образом, если сила перпендикулярна к элементарному перемещению (то есть к вектору скорости ее точки приложения) то ее элементарная работа равна нулю.

Из кинематики точки известны следующие соотношения:

; ;,

Учитывая их, получим

.

Подставляя это выражение в формулу (4.30), получим

, (4.31)

где - дифференциал от радиус-вектора точки, считается направленным по касательной.

Таким образом, элементарной работой силы называют скалярную величину, равную скалярному произведению силы на дифференциал радиус-вектора точки приложения этой силы.

Учитывая, что , получим

, (4.32)

где - элементарный импульс силы.

Если силу и радиус-векторразложить по осям координат, получим

,

,

.

Подставляя полученные равенства в выражение (4.31), получим аналитическое выражение для элементарной работы силы

. (4.33)

Полученное выражение (4.33) называют аналитическим выражением для элементарной работы силы.

6.2. Полная работа силы

Рассмотрим конечное перемещение точки из положения М₀ в М положение (рис. 19). Разобьём это конечное перемещение на n элементарных бесконечно малых перемещений.

Тогда полная работа силы на конечном перемещении точки приложения из начального положенияМ₀ в конечное М определяется по формуле

. (4.34)

Используя выражения (4.29), (4.31) и (4.33), получим

(4.35)

, (4.36)

. (4.37)

Выражение (4.37) называют аналитическим выражением для полной работы силы на конечном перемещении точки приложения из начального положения М₀ в конечное М.

Если на материальную точку действует система сил , то элементарная работа равнодействующей силы определяется по формулам

,

, (4.38)

где - равнодействующая сила.

Формула (4.38) выражает важное свойство полной и элементарной работы силы. Это свойство можно сформулировать следующим образом: работа равнодействующей силы на элементарном или конечном перемещении равна сумме работ совершаемых всеми силами, образующими эту равнодействующую на этом же перемещении.

Если сила не меняется по величине и угол φ между этой силой и вектором скорости остается постоянным, то из формулы (4.35) получим

. (4.39)

В системе единиц СИ работа измеряется в джоулях,

Дж.