3.5. Частные случаи теоремы об изменении количества движения для системы (Законы сохранения количества движения)

При применении теоремы об изменении количества движения системы выделяют два частных случая, в зависимости от особенностей системы внешних сил, действующих на рассматриваемую механическую систему. Эти частные случаи получили название законов сохранения количества движения. Рассмотрим эти законы.

1. Первый закон сохранения количества движения.

Если главный вектор внешних сил системы равен нулю, то вектор количества движения системы постоянен по величине и направлению.

Таким образом, если , то справедливо

. (4.14)

Проецируя на координатные оси, получим

,,, (4.14^/)

где,,– постоянные величины.

В соотношения (4.14) и (4.14/) входят производные от координат точек по времени не выше первого порядка. То есть, эти соотношения являются первыми интегралами системы дифференциальных уравнений (4.3).

2. Второй закон сохранения количества движения системы.

Если проекция главного вектора всех внешних сил системы на какую-либо ось (например Ox) равна нулю, то проекция вектора количества движения системы на эту же ось является постоянной величиной.

Таким образом, если 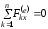, то справедливо

. (4.15)

4. Теорема о движении центра масс системы. Дифференциальные уравнения поступательного движения твердого тела

4.1. Теорема о движении центра масс системы

Теорема о движении центра масс системы является следствием теоремы об изменении количества движения систем.

По теореме об изменении количества движения системы (4.11) имеем

.

Количество движения системы можно определить по формуле (4.6)

,

где - масса системы,

- вектор скорости центра масс системы.

Подставляя (4.6) в (4.11) и учитывая, что масса системы постоянна, получаем теорему о движении центра масс в векторной форме:

, или

, (4.16)

где – ускорение центра масс системы.

Теорема о движении центра масс системы формулируется следующим образом: центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.

Проецируя (4.16) на оси декартовой системы координат, получим дифференциальные уравнения движения центра масс системы:

,

, (4.16^/)

,

где ,,– координаты центра масс системы.

Рассмотрим два следствия из теоремы о движении центра масс системы.

1. Следствие 1.

Если главный вектор внешних сил, действующих на систему, равен нулю , то из формулы (4.16) следует, что ускорение центра масс системы также равно нулю, то есть вектор скорости центра масс не меняется ни по величине ни по направлению. Если, в частности, в начальный момент времени центр масс механической системы неподвижен, то его положение не меняется в течение всего времени, пока главный вектор внешних сил равен нулю.

2. Следствие 2.

Если проекция главного вектора внешних сил, действующих на систему, на какую-либо из осей (например на ось Ox), равна нулю 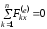, то из формулы (4.16^/) следует, что проекция ускорения центра масс на эту же ось также равна нулю , то есть проекция скорости центра масс на эту ось является постоянной величиной:.

Следует обратить внимание, что внутренние силы не влияют явно на движение центра масс. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных ее частей и, следовательно, изменить взаимодействие с внешними телами, вызывая этим реакции связей (внешние силы). Эти силы реакций могут изменить движение центра масс или вывести его из равновесия.