
podyak
.pdfса исходит из прямого преобразования Фурье, в котором комплексный оператор j заменяется оператором p = + j , носящим название комплексной частоты. Использование его позволяет перейти от решения системы дифференциальных уравнений к решению более простой системы алгебраических уравнений.
Пусть некоторая функция f(t) определена при t 0 и тождественно равна нулю при t 0. Для нее преобразование Лапласа записывается в следующем виде:
|
|
F ( p) f (t)e pt dt . |
(1.21) |
0 |
|
Функцию f(t) называют оригиналом, а функцию F(p) – ее изображением. Зная изображение функции, можно восстановить ее оригинал с помощью обратного преобразования Лапласа, сходного с обратным пре-
образованием Фурье:
|
1 |
j |
|
|
f (t) |
|
F ( p)e pt dp. |
(1.22) |
|
2π j |
||||
|
j |
|
||
|
|
|
Решение последнего уравнения детально исследуется в теории функций комплексного переменного и может быть получено во многих случаях с помощью следующего алгоритма, называемого теоремой разложения.
Смысл ее состоит в следующем. Пусть изображение искомой функции имеет вид
F ( p) |
A( p) |
, |
(1.23) |
|
B( p) |
||||
|
|
|
где А(p), B(p) – полиномы комплексной переменной p степеней m и n, причем m n:
A(p) = ampm + am–1pm–1 + am–2pm–2 +…a0, |
(1.24) |
B(p) = bnpn + bn–1pn–1 + an–2pn–2 +…b0. |
(1.25) |
Предполагается также, что коэффициенты a, b – действительные числа и полиномы A(p), B(p) не имеют общих корней.
Вынося коэффициент bn при старшей степени p полинома B(p), представим новый полином B1(p) в виде произведения простых сомножителей:
11
F ( p) |
A( p) |
|
|
|
|
A( p) |
|
|
|
, |
(1.26) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
bn B1 |
( p) |
|
bn |
( p p1 ) |
s1 |
( p p2 ) |
s2 |
...( p pq ) |
sq |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
где p1, p2, …, pq – корни характеристического уравнения B1(p) = 0; s1, s2, …, sq – числа, определяющие кратность корней полинома B1(p).
Следующим шагом является разложение функции F(p) на простые составляющие по формуле
|
1 |
q |
sk |
Kki |
|
|
|
|
F ( p) |
|
|
|
|
|
|
, |
(1.27) |
|
s |
|
i 1 |
|||||
|
|
|||||||
|
bn k 1 i 1 |
( p pk ) |
k |
|
|
|
||
в которой коэффициенты Kki рассчитываются по следующему соотношению:
|
|
|
|
(i 1) |
|
|
|
|
|
|
|
||
K |
1 |
|
d |
|
|
(p p |
)sk F (p) |
, |
p p , |
i 1, 2,..., s . (1.28) |
|||
|
|
|
|
i 1 |
|||||||||
ki |
(i 1)! |
|
|
|
k |
|
|
|
k |
k |
|||
|
dp |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поясним сказанное на примере функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
F ( p) |
|
5( p 1) |
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
p( p |
2)2 ( p 4) |
|
|
|
|
|
|
|
|||||||||||
1. |
Записываем исходную функцию в виде суммы простых дробей: |
|||||||||||||||||||||||||||||
|
F ( p) |
K1 |
|
|
|
K21 |
|
|
|
|
K22 |
|
|
|
|
K3 |
|
. |
(1.29) |
|||||||||||
|
|
|
( p 2)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
p |
|
|
|
( p 2) |
|
p |
4 |
|
|
||||||||||||||||
2. |
По формуле (1.29) находим коэффициенты: |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
K |
pF ( p) |
|
|
|
|
|
5 |
, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
p 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
K |
|
|
( p 2)2 F ( p) |
|
|
|
|
5 |
, |
|
|
|
|
||||||||||||||||
|
21 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
4 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
5( p 1) |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||||||
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||
|
22 |
|
p( p 4) |
|
|
|
|
4 |
|
|
|
|||||||||||||||||||
|
|
|
dp |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|||||||||
12

K3 ( p 4)F ( p) p 4 1615 .
Для нахождения оригиналов полученных выражений обратимся к табл. 1.1 соответствия между ними и их изображениями для часто встречающихся временных функций. Воспользовавшись данными 2, 3 и 9 строк, запишем уравнение искомой функции времени:
|
|
|
|
|
|
s(t) |
|
5 |
|
|
15 |
e 4t |
5 |
e 2t |
5 |
e 2t |
|||||||||||||||
|
|
|
|
|
|
16 |
16 |
4 |
4 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а 1.1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Функция времени |
|
|
|
|
|
|
Преобразованная функция |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. (t) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
2. (t) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. 1 – e |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( p ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 2 |
|||||||||||
6. sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 2 |
|||||||||||
7. kt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
||||||||
8. tn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn 1 |
|||||||||
|
|
t |
n 1 |
pk t |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||
9. |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(p p )n |
|||||||||||||||
|
(n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||||
10. |
d s(t) |
|
|
|
|
|
|
|
|
|
|
|
ps( p) s(0) |
||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13

t |
s(p) |
(0) |
11. s(t)dt |
|
|
|
p |
|
p |
|
0 |
|
||
|
|
|
Примечание. В строках 10, 11 через s(0) и (0) обозначены соответственно
начальные значения функции и ее оригинала.
1.5. ФУНКЦИИ ЭЛЕКТРОННОЙ ЦЕПИ. КОМПЛЕКСНЫЙ И ОПЕРАТОРНЫЙ КОЭФФИЦИЕНТЫ ПЕРЕДАЧИ
Обратимся к рис. 1.1 и введем следующие параметры, позволяющие судить о свойствах электронной цепи, представленной в виде четырехполюсника:
Z |
|
|
|
|
Uвх |
|
|
– комплексное входное сопротивление цепи; |
||||||
вх |
Iвх |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z |
|
|
|
|
|
Uвых |
– комплексное выходное сопротивление цепи, опреде- |
|||||||
вых |
|
|
|
|||||||||||
|
|
|
Iвых |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
ляемое как входное со стороны выходных зажимов цепи; |
||||||||||||||
KU |
( j ) |
|
Uвых |
– комплексный коэффициент передачи по напря- |
||||||||||
|
|
Uвх |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
жению; |
|
|
|
|
|
|
|
|
|
|||||
K |
|
( j ) |
Iвых |
|
– комплексный коэффициент передачи по току. |
|||||||||
I |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Iвх |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Все названные параметры определяются при подаче на вход цепи сигнала гармонической формы, который представляется в символической форме
f (t) Acos( t ) Ae j ( t ) Ae j e j t |
|
Ae j t , |
где Ae j A – комплексная амплитуда гармонического сигнала.
Из сказанного следует, что все функции цепи будут комплексно зависимыми от частоты входного сигнала. Обращаясь в частности к коэффициенту передачи по напряжению KU, удобно записать его в форме
комплексной величины: |
|
K ( j ) K ( )e j ( ) , |
(1.30) |
14

где K( ) – модуль комплексного коэффициента передачи по напряжению; ( ) – фаза комплексного коэффициента передачи.
Соответствующие зависимости от частоты называются амплитудночастотной характеристикой (АЧХ) и фазочастотной характеристикой
(ФЧХ).
Для их определения надо иметь принципиальную схему цепи, с помощью законов электротехники рассчитать параметры ее электрического состояния и через них выразить требуемые функции цепи.
В целом ряде практических задач возникает необходимость установить временную связь между входным и выходным сигналами. Одним из распространенных здесь приемов является применение преобразования Лапласа, позволяющее входную функцию времени и комплексную функцию коэффициента передачи привести в одну систему координат и решить задачу сначала в области комплексной переменной p, а затем перенести решение во временную область. Последовательность действий при этом:
1)переводим временной входной сигнал в операторную форму;
2)переводим комплексный коэффициент передачи K(j ) формальной заменой оператора j на оператор р;
3)находим операторное выражение выходного сигнала по формуле
Uвых ( p) Uвх ( p) K ( p) j p , |
(1.31) |
где p j ;
4)используя известные методы нахождения оригинала функции по
ееизображению, находим временной образ выходного сигнала.
(Отметим, что записанный в операторной форме комплексный коэффициент передачи называется передаточной функцией.) Особое значение при анализе передаточных свойств электронной цепи имеет переходная характеристика, под которой понимается отклик цепи на входной сигнал, представляющий собой функцию единичного скачка
(t). С помощью переходных характеристик обычно рассчитывают определяющие параметры переходного процесса и устанавливают их связь с параметрами элементов цепи.
Приведем несколько примеров нахождения частотных и временных зависимостей в конкретных цепях.
Пример 1.3. Получить выражения комплексного |
UВЫХ |
|
R |
||
коэффициента передачи, АЧХ и ФЧХ, переходной |
||
UВХ |
||
характеристики для цепи, изображенной на рис. 1.3. |
C |
|
|
Рис. 1.3 |
15
1. В этой цепи комплексный коэффициент определяется отношением емкостного сопротивления к полному входному сопротивлению:
1
K ( j ) 1 j RC .
1
2. Амплитудно-частотная характеристика (АЧХ): K ( )  .
.
1 ( RC)2
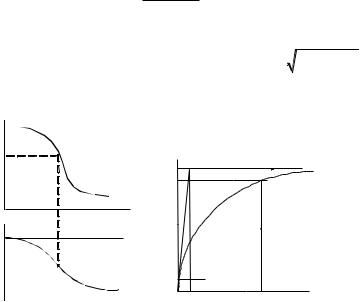
3. Фазочастотная характеристика (ФЧX): ( ) = –аrctg RC. Графики полученных зависимостей показаны на рис. 1.4.
1 |
к |
|
|
|
|
|
|
0.7 |
|
( t) |
|
|
|
|
|
|
|
1 |
|
|
|
0.9 |
|
|
в |
|
|
|
|
|
|
- /4 |
|
|
|
|
|
0.1 |
t |
- /2 |
|
|
|
|
|
tф н |
|
|
|
||
|
Рис. 1.4 |
|
Рис. 1.5 |
Обратим внимание на значение частоты в, называемой верхней граничной частотой. На этой частоте коэффициент передачи цепи уменьшается в корень из двух раз, т. е. составляет величину 0.7 от максимального значения. Частота в определяется из равенства
вRC = 1:
в = 1/RC. |
(1.32) |
Граничная частота условно разделяет область нижних ω < ωв и область ω > ωв верхних частот. В области нижних частот цепь пропускает сигнал почти без ослабления, поэтому ее называют фильтром нижних частот. В области верхних частот сигнал ослабляется почти обратно
16

пропорционально частоте. Еще одно замечательное свойство цепи состоит в способности осуществлять операцию интегрирования входного сигнала при условии выполнения неравенства RC >> 1. В этом случае выходное напряжение на конденсаторе оказывается пропорциональным интегралу от входного напряжения.
Частотные и временные характеристики связаны между собой. При подаче функции включения (t) на вход цепи выходное напряжение принимает операторный образ:
Uвых (p) |
1 |
|
1 |
. |
(1.33) |
|
|
||||
|
p 1 pRC |
|
|||
Полученному изображению соответствует оригинал (строка 3 в
табл. 1.1):
|
t |
|
|
|
|
h(t ) 1 e |
RC . |
|
Зависимость выходного напряжения от времени и есть переходная характеристика рассматриваемой цепи (рис. 1.5), представляющая собой экспоненциально нарастающую кривую, начинающуюся от нулевого начального значения и стремящуюся к установившемуся значению 1. Зависимость характеризуется также временем нарастания фронта tфн, когда выходное напряжение изменяется от 0.1 до 0.9 своего максимального значения:
tфп = 2.2 RC,
где произведение RC τ называется постоянной времени цепи. Касательная к функции h(t) в точке t = 0 определяет максимальную скорость изменения переходной характеристики, равную V 1 . Напом-
. Напом-
ним, что цепь подобного вида определялась ранее с точки зрения частотных свойств как фильтр низших частот и характеризовалась зна-
чением верхней граничной частоты в RC1 . Сопоставив два послед-
них соотношения, получим полезный для практики результат, устанавливающий связь между частотными и временными искажениями:
17
C
UВЫХ
UВХ R
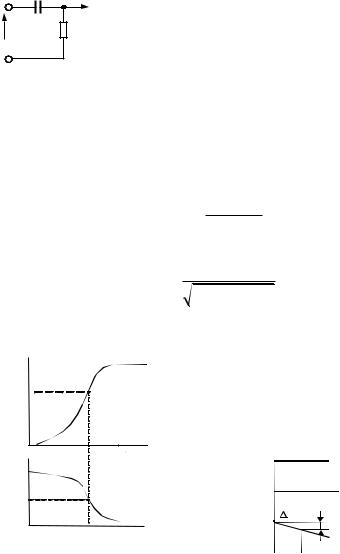
Рис. 1.6
2.2
tфн в .
Чем больше постоянная времени RC, т. е. меньше полоса пропускания цепи, тем медленнее изменяется выходное напряжение на емкости в процессе достижения своего установивше-
гося значения.
Пример 1.4. Получить выражения комплексного коэффициента передачи, АЧХ и ФЧХ, переходной характеристики для цепи, изображенной на рис. 1.6.
1. В этой цепи комплексный коэффициент определяется отношением емкостного сопротивления к полному входному сопротивлению:
j RC
K ( j ) 1 j RC .
2. Амплитудно-частотная характеристика:
1
K ( ) .

 1 1 / ( RC)2
1 1 / ( RC)2
3. Фазочастотная характеристика: ( ) = аrctg (1/ RC). Графики полученных зависимостей приведены на рис. 1.7.
1 к |
|
|
|
|
0.7 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
н |
|
1 |
U ВХ |
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
/4 |
|
|
U ВЫХ |
|
|
|
|
U ВЫХ |
|
|
|
|
1 |
|
|
н |
|
|
|
|
|
|
||
|
|
|
|
t |
|
Рис. 1.7 |
|
|
Рис. 1.8 |
18

Обозначенная на АЧХ частота н называется нижней граничной частотой. На этой частоте коэффициент передачи уменьшается в корень из двух раз, т. е. примерно 0.7 от максимального значения коэффициента передачи:
н = 1/RC. |
(1.35) |
Способность цепи подавлять нижние частоты, содержащиеся в спектре входного сигнала, делают понятным отнесение ее к классу «фильтров высших частот».
Если выбрать величины элементов схемы таким образом, что Uвх >> UR, то общий ток цепи сделается приблизительно равным
i С |
dUC |
C |
dUвх |
|
Uвых |
. |
(1.36) |
|
|
|
|||||
С |
dt |
|
dt |
|
R |
|
|
|
|
|
|
||||
А это в свою очередь означает, что выходное напряжение оказывается пропорциональным производной входного сигнала, что позволяет назвать цепь дифференцирующей. Способность цепи подавлять нижние частоты, содержащиеся в спектре входного сигнала, делает понятным отнесение ее к классу «фильтров высших частот». Применительно к гармоническому входному сигналу условие дифференцирования означает обеспечение неравенства
1 |
R или RC << 1. |
(1.37) |
|
С |
|||
|
|
Если же входной сигнал представляет более сложную функцию, то для операции дифференцирования необходимо выполнить условие дифференцирования для гармоники самой низкой частоты, входящей в состав спектра входного сигнала.
4. Переходная характеристика цепи. Преобразованная по Лапласу комплексная передаточная функция имеет вид
pCR
K (p) 1 pCR .
При подаче сигнала (t) выходное напряжение, выделяемое на резисторе R и представляющее собой переходную функцию, запишется в операторной форме:
19
h( p) |
CR |
, |
||
|
|
|||
1 pCR |
||||
что соответствует оригиналу: |
|
|
|
|
|
|
t |
|
|
h(t ) e |
RC . |
(1.38) |
||
График этой функции, показанный на рис. 1.8, представляет собой затухающую экспоненту с максимальным значением, равным 1.
В некоторый произвольный момент времени tи выходное напряжение уменьшится на величину Uвых:
|
|
|
|
|
tи |
|
|
|
|
|
U |
вых |
1 e |
RС . |
(1.39) |
||
|
|
|
|
|
|
|
||
Отношением |
Uвых |
100 % |
принято характеризовать степень ис- |
|||||
Uвых max |
||||||||
|
|
|
|
|
|
|
||
кажения переходной характеристики рассматриваемой цепи, что при RC >> tи дает следующий результат:
Uвых |
|
tи |
|
100 % , |
(1.40) |
|
Uвых max |
RC |
|||||
|
|
|
||||
Uвых |
t 100 % , |
(1.41) |
||||
|
||||||
Uвых max |
|
и н |
|
|
||
|
|
|
|
|
||
что еще раз подчеркивает взаимную связь частотных и временных параметров.
С уменьшением значения постоянной времени цепи = RC cкорость спада выходного напряжения увеличивается, и оно приобретает форму затухающего импульсного скачка конечной длительности.
1.6. УПРАЖНЕНИЯ К РАЗДЕЛУ 1
1. Поясните понятия комплексного коэффициента передачи, ампли- тудно-частотной и фазочастотной характеристик электронной цепи.
2. Дайте определение переходной характеристики электронной цепи.
20
