Примеры числовых множеств:

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

16.1.4. Правило Лопиталя – Бернулли

Это правило описывает раскрытие неопределенностей типа

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северный государственный медицинский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1 кур 5 лет / Менеджмент / Математика / kurs_vysshey_matematiki.pdf

Скачиваний:

Добавлен:

25.03.2015

Размер:

9.85 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

94							.	ru	Лекции 8 – 9
94									Лекции 8 – 9
		Числа вида		m	: m	, n	образуют множество рациональ-
	О			m
	О		= q =	n

ных чисел.

antigtu

< n ,

правильной, если

Если

то рациональная дробь называется

≥ n – неправильной.

Рациональные дроби представляются в виде конечных или бесконечных

периодических десятичных дробей после деления числителя на знаме-

натель.

Пример:

1 = 0,333... = 0,(3) ,

= 0, 4 = 0,3999... = 0,3(9) ,

= 0,0707... = 0,(07) .

О Числа, выражающиеся бесконечной непериодической десятичной дробью, составляют множество иррациональных чисел I . Например,

			с
	2 =1,41... , π = 3,14159265359..., e = 2,71828 18284 59045... .
О	Рациональные и иррациональные числа составляют множество действи-
	тельных чисел = I .
!	Между множеством дей твительных чисел и множеством точек число-
	Скачано
	вой прямой существует взаимно-однозначное соответствие.
8.3. Числовые пр межутки
	Примеры числовых множеств:
	Множество элеме тов x:		x
	Множество элеме тов x:		{	}
	Элемент множества:		x {x}
	Отрезок (сегмент):		x =		[	a,b	]	: a ≤ x ≤b, где a	x ,b	x
	Отрезок (сегмент):		{	}	[		]		{ }	{ }
	Интервал:		{x}= (a,b): a < x < b
Полуинтерв л (полусегмент):				{x} = (a, b]: a < x ≤ b,
Полуинтерв л (полусегмент):				{x} =[a, b): a ≤ x < b,
				{x} =[a, b): a ≤ x < b,
		Луч:		{x} =[a, ∞) : (x ≥ a)
		Луч:		{x} = (−∞, b]: (x ≤ b)
				{x} = (−∞, b]: (x ≤ b)

Элементы теории множеств и математической логики. Числовые последовательности

Окрестность точки c - это произвольный интервал

(a,b), содержащий точку с.

Эпсилон – окрестность точки с. {x :

x − c

<ε}

или c −ε < x < c + ε .

8.4. Ограниченные множества

Множество {x}

называется ограниченным сверху, если существует та-

кое число М, что x {x}: x ≤ M , где М называется верхней гранью мно-

жества {x}

(ВГ {x}).

Пример:

{

−1, 2,3, 4,5

, M

= 5,

= 6,

=10,....

}

antigtu

{ }

Т Ограниченное сверху множество имеет бесконечное число верхних гра-

ней.

Наименьшая из всех верхних граней называется точной верхней гра-

нью x = Sup x

(от латин кого supremum - наивысшее) (ТВГ x ).

Пример:

Скачано

{−1, 2,3, 4,5}, x = 5 .

Множество {x}

называется граниченным снизу, если существует та-

кое число m, что x {x}: x ≥ m , где m – нижняя грань {x} (НГ {x}).

Ограниченное с изу м ожество имеет бесконечное число нижних гра-

ней.

Наибольш я из всех нижних граней называется точной нижней гранью

x = Inf {x} (от латинского infimum - наинизшее) (ТНГ {x}).

Множество {x}

называется ограниченным, если существует число

М > 0 т кое, что x {x}:

≤ M . Ограниченное множество является

одновременно ограниченным и снизу, и сверху.

Множество {x}называется неограниченным, если для любого сколь

угодно большого числа М > 0 найдется элемент x {x}, удовлетворяю-

щий неравенству:

≥ M .

Лекции 8 – 9

Пример:

Неограниченные множества:

(-∞,∞) – неограниченное множество,

(-∞,2] – неограниченное снизу множество,

[-5,∞) -

неограниченное сверху множество.

antigtu

Для того чтобы множество было неограниченным, достаточно, чтобы

оно было неограниченным либо сверху, либо снизу.

{x},

Число

называется

наибольшим

элементом

множества

M =max{x}, если 1) M {x}; 2) x {x}: x ≤M .

{x},

Число

называется

наименьшим

элементом

множества

m = min{x}, если 1) m {x}; 2) x {x}: x ≥ m .

Ограниченное сверху (снизу) множество может иметь наибольший (наи-

меньший) элемент, а может и не иметь его:

{x} =[a;b]

, max{x}=b, min{x} = a ;

{x} = (a;b),

max{x},

min{x} не существуют.

8.5. Числовые последовательности

Если каждому натуральному чи лу n по определенному закону постав-

Скачано

xn ,

то

множество

лено

соответствие

некоторое

число

{

{ 1

}

1 2

x , x

, x ,....x

,...

нумерсванных чисел x , x , x ,.... называется чи-

словой послед вательн стью. Элементы этого множества называются

членами или элементами п след вательности.

Числовая последователь ость может быть задана:

1) перечисле ием элеме тов;

2) зад нием общего члена последовательности как функции номера

xn = f

(n);

3) в виде рекуррентных (возвратных) соотношений; в этом случае за-

дается несколько первых членов последовательности и закон, по кото-

рому вы исляются последующие члены:

xn+1 = f (xn ),

x1 = const -

одно-

членн я рекуррентная формула, xn+2 = f (xn+1, xn ),

x1 = c1,

x2 = c2

- дву-

членн я рекуррентная формула, и т.д.

Элементы теории множеств и математической логики. Числовые последовательности																			97
Пример:
Пример:
	3)	{1, 2,3,...} = {n};															.	ru
	1)	{−1,1, −1,1,...}={(−1)n }												;
	2)		1	,	2						n −1
	2)	0,	2	,	3		,...			=		n	;			antigtu
			2		3							n
						xn									1
	4)	x	=			xn		,	x		=1		x	=	1	, n =1, 2,3,...;
	4)	x	=					,	x		=1		x	=		, n =1, 2,3,...;
		n+1			2				1				n		2n−1
					2										2n−1
	5)	xn+2 = xn+1 + xn ,										x1 =1,		x2	=1	x3 = 2, x4 = 3,...

Если рассмотреть произвольную возрастающую последовательность на-

туральных чисел: k1,k2 , k3 ,....kn ,...

и выбрать из последовательности {xn}

ее члены с соответствующими номерами xk , xk

,...,xk ,... то полученная по-

следовательность называется подпоследовательностью последователь-

ности {xn}. Например, для произвольной последовательности подпосле-

довательностями являются последовательности четных или нечетных

членов.

Числовые последовательности являются

упорядоченными числовыми

множествами, для них

праведливы теоремы об ограниченных множест-

вах.

Пример:

Скачано

Последовательность

{ n }

{

}

{

−1, −2,

}

ограничена сверху,

−n

−3,... −n,...

поскольку все члены эт й п следовательности удовлетворяют неравенству

xn ≤ −1.

Последователь ость {xn } ={n2 }

ограничена снизу, т.к. xn = n2 ≥1 .

Последователь ость

ограничена. Для

любого

n N 0 < 1 ≤1, т.е.

M =1, m = 0 .

Пример:

Неограни енные последовательности:

1) {xn } ={n2 }. При любом M > 0 достаточно взять n > M .

2) {(1 − (−1)n )n}. Среди нечетных всегда найдется член, удовлетворяющий

условию

≥ M для любого M > 0 .

98 Лекции 8 – 9

8.6. Свойства ограниченных последовательностей

Сумма двух ограниченных последовательностей есть последователь-

ность ограниченная.

Разность двух ограниченных последовательностей есть последова-

тельность ограниченная.

Произведение двух ограниченных последовательностей

есть после-

довательность ограниченная.

Неограниченные последовательности таких свойств не имеют.

9.1. Предел числовой последовательности

Конечное число a называется пределом числовой последовательности

{xn}(обозначается

lim xn = a или

→ a ),

если для любого положи-

n→∞

→∞

тельного числа ε

найдется такое натуральное число

N (зависящее от

ε ), что при всех n > N выполняется неравенство

xn − a

<ε .

Это может быть описано также в следующих терминах:

последовательность

{xn

}

сходится к

;

последовательность

{xn

} имеет предел, равный a ;

antigtu

xn (общий член по ледовательно ти) стремится к a .

Сокращенная запись:

lim x = a

ε > 0 N = N (ε ): n > N (ε )

x − a

< ε

(n→∞ n

)

(

)

Последовательн сть,

имеющая конечный предел, называется сходящей-

ся.

То же утвержде ие может быть сформулировано короче.

Число a есть предел последовательности {xn}, если ее члены отли-

чаются от a сколь угодно мало, начиная с некоторого места.

Исходное определение уточняет, как следует понимать «сколь угодно

мало» и «н чин я с некоторого места».

ε > 0

xn − a

< ε -

точная

формулировка первого утверждения, а n > N (ε ) -

второго

Пример:

Д но: {xn }

n −1

lim xn = lim

n −1

−

= lim 1

= 1.

n→∞

До ажем, что lim

−

=1.

n→∞

Доказательство:

Скачано

Элементы теории множеств и математической логики. Числовые последовательности																																99
									ε > 0,	n −1 −1 <				ε 1 −									1		− 1 < ε;	1	< ε, n >		1
									ε > 0,	n −1 −1 <				ε 1 −									1		− 1 < ε;	1	< ε, n >		1
										n													n			n			ε
		Если				взять			N (ε )	– любое				целое,									большее,				чем	1	,	то неравенство
																												ε		.	ru
			n −1			−1	< ε		будет выполнено					n > N (									ε ), ч.т.д.
			n −1
				n
						Геометрическая интерпретация примера:
						Геометрическая интерпретация примера:

					0						1				2			3		4			5		1
					x1					2					3				4		5			6
					x1					x				x3			x4			x5				x6
										2
				− ε < x n − 1 < ε , 1 − ε < x n < ε + 1 .
		ε =			1			1	= 2; n > 2				xn −1	<		1		.
					1			1								1
						, N
					2			2								2
		ε =			1			1	= 5; n > 5			xn −1		<	1		.
					1			1							1
						, N
					5			5							5
	Последовательность {(−1)n} не имеет предела,
!	Последовательность {(−1)n} не имеет предела,																										так как нельзя указать
																						antigtu
																						antigtu
	номер, после которого в е члены по ледовательности окажутся в сколь
	угодно малой окрестно ти какого-либо числа.

О Последовательности, не имеющие предела, называются расходящими-

ся.

9.2. Бесконечно большие и бесконечно малые

последователь ости

Последов тельность {xn}

называется бесконечно большой, если для

любого положительного

числа M

можно

указать

такое натуральное

число N (зависящее от M ), что при всех n > N выполняется неравенст-

во

> M .

M > 0 N = N (M ): n > N (M )

> M .

Если числов я последовательность {xn} бесконечно большая и ее члены

(по райней мере, начиная с какого-то номера) сохраняют определенный

знак ( + или −), говорят, что последовательность {xn}

имеет предел +∞

(или −∞ ): lim x

= +∞ , x

→ +∞ или lim x

= −∞ , x

→ −∞.

n→∞

n→∞ n

n→∞

Скачано

100

Лекции 8 – 9

Пример:

Последовательности

{nα }, α > 0 , являются бесконечно большими, т.к.

для любого M > 0 из nα > M следует, что если n > α M , то условие оп-

ределения выполнено.

Последовательность {xn}

называется бесконечно малой, если для лю-

бого сколь угодно малого положительного числа ε найдется такое нату-

ральное число N (зависящее от ε ), что при всех n > N

(ε) выполняется

неравенство

<ε .

( ε > 0 N (ε ): n > N (ε ):

< ε ).

Из определения предела последовательности следует, что последова-

тельность {xn} бесконечно мала, если lim xn = 0 .

Пример:

n→∞

Бесконечно убывающая геометрическая прогрессия

= qn ,

<1, явля-

ется бесконечно малой последовательностью, т.к. для любого ε > 0 из

неравенства

q n

< ε

следует, что при n > log

ε это неравенство выпол-

[log

ε].

нено, т.о. N (ε

) =

antigtu

9.3. Свойства бесконечно малых последовательностей

Бесконечно малая п след вательность ограничена.

Доказательство:

Пусть {xn} – беско еч о малая последовательность. Тогда для данного

ε , начиная с

екоторого

омера, имеет место неравенство

<ε . Вы-

бирая в качестве M максимальное из чисел ε,

,...,

xn −1

, получим

< M для всех n , что и требовалось доказать.

Сумма двух

бесконечно

малых последовательностей есть последова-

тельность бесконечно малая.

Р зность двух бесконечно малых последовательностей есть последова-

тельность бесконечно малая.

Произведение ограниченной последовательности на бесконечно малую

есть последовательность бесконечно малая.

Скачано

						ru	101
Элементы теории множеств и математической логики. Числовые последовательности							101
Доказательство:					.
Пусть {xn} – бесконечно малая, а {yn} – ограниченная последовательно-
сти, т.е. для любого ε > 0 существует N (ε) такое,				что для		n > N (ε)
		antigtu
	xn	<ε , и существует такое число M , что для всех	n	yn	< M	Тогда для
		последовательности {xn yn} при n > N (ε) имеем	xn yn		< ε M		Так как
	M – фиксированное число, а ε – сколь угодно малое, то ε M также
сколь угодно малое. Теорема доказана.

Произведение двух бесконечно малых последовательностей есть после-

довательность бесконечно малая.

Справедливость этого утверждения следует из того, что бесконечно ма-

лая последовательность всегда ограничена.

Если элементы бесконечно малой последовательности {xn}

не равны

нулю, то последовательность

будет бесконечно большой.

Если {xn} бесконечно большая последовательность и xn ≠ 0 ,

то после-

довательность

– бесконечно малая.

Пример:

1). Последовательно ть

sin n

– бе конечно малая,

т.к. ее элементы яв-

Скачано

ляются произведением

элементов

ограниченной

последовательности

{sin n} и беск нечно мал й псследовательности

2). Последовательн сть

n +1

– бесконечно малая, т.к. является суммой

бесконеч о малых последовательностей

−n

3). Последов тельность

– бесконечно малая, т.к. является произве-

дением бесконе но малой последовательности {e−n } на бесконечно малую

последовательность

Последов тельность {xn}

называется фундаментальной, если для лю-

бого положительного ε > 0 найдется номер N (ε)

такой, что для всех n ,

удовлетворяющих условию n > N (ε),

и для всех натуральных чисел m

( m =1,2,3,...) справедливо неравенство

xn+m − xn

< ε.

ε > 0 N (ε) : n > N (ε) m N : xn+m − xn < ε .

102

Лекции 8 – 9

Критерий Коши. Для того чтобы последовательность {xn}

была сходя-

щейся, необходимо и достаточно, чтобы она была фундаментальна.

antigtu2 n

9.4. Свойства сходящихся последовательностей

1º.

Элементы сходящейся последовательности имеют вид:.xn = a +αn ,

где

{

– бесконечно малая последовательность.

Доказательство:

По определению предела ε > 0 N (ε ): n > N (ε ),

xn − a

< ε .

Рассмотрим αn = xn − a xn = a +αn , подставим

a +αn − a

< ε ε > 0 N (ε) : n > N (ε)

αn

< ε , т.е.

limαn = 0 αn - бесконечно малая последовательность.

n→∞

2º.

Сходящаяся последовательность имеет только один предел.

Доказательство:

Пусть a = lim x и b = lim x ,

≠ b ,

< r < b – два предела сходящейся

n→∞ n

n→∞

последовательности {xn }.

ε > 0 N1 : n > N1

xn − a

r − a

n > N1 xn < r ;

ε > 0 N : n > N

x −b

b − r

n > N x > r .

Выберем

N = N (ε )

max{N1 ,N2} и

n ≥ N : тогда должно одновременно

Скачано

xn > r , что невозможно, значит, a = b .

выполняться

xn < r

3º.

Сходящаяся п след вательнссть ограничена.

Обратное

утверждение

неверно,

например,

последовательность

{xn} =

πn

sin

является ограниченной, но предела не имеет.

4º.

Сумма, разность, произведение и

также частное (при условии,

что

≠ 0 и lim yn ≠ 0) двух сходящихся последовательностей {xn} и

n→∞

{yn} есть сходящ яся последовательность, и ее предел равен соответст-

венно сумме, разности, произведению и частному пределов исходных

последовательностей.

Док з тельство (сумма):

Пусть

{xn}

и {yn

}

– сходящиеся

последовательности

lim xn

= a ,

n→∞

lim yn

= b . Тогда xn = a +αn ,

yn = b + βn где {αn}

и {βn} – бесконечно

n→∞

xn + yn = a +b +αn + βn , т.е.

последова-

малые

последовательности, и

тельность {xn + yn − a −b}

– бесконечно малая, и поэтому {xn + yn}

схо-

дится и имеет своим пределом a + b .

Элементы теории множеств и математической логики. Числовые последовательности										103
	Арифметические операции над сходящимися последовательностями
С
С	приводят к таким же операциям над их пределами.
	приводят к таким же операциям над их пределами.
	5º.	Если элементы сходящейся последовательности {xn}, начиная с не-
	которого номера, удовлетворяют неравенству xn ≤ b ( xn ≥ b ), то и предел
	этой	последовательности		lim xn ≤ a удовлетворяет			неравенству			a ≤ b
	( a ≥ b ).			n→∞				.	ru
									ru

									{xn} и {yn},
С	1. Если элементы xn		и yn	сходящихся последовательностей					{xn} и {yn},
	начиная с некоторого номера,				удовлетворяют неравенству xn ≤ yn , то их
	пределы удовлетворяют такому же неравенству: lim xn							≤ lim yn .
						n→∞		n→∞
	2. Если все элементы сходящейся последовательности {xn} находятся на
	отрезке [a;b], то и ее предел также находится на этом отрезке.
6º.	Пусть {xn} и {zn} – сходящиеся последовательности и lim xn = lim zn = a .
								n→∞	n→∞
	Пусть, начиная с некоторого номера, элементы последовательности {yn}
	удовлетворяют неравенствам					xn ≤ yn ≤ zn .Тогда последовательность
	{yn}	сходится и lim yn = a .
7º.		n→∞
7º.	Любая подпоследовательность сходящейся последовательности сходит-
	ся к тому же пределу.					antigtu
						antigtu
9.5. Монотонные последовательности
				с
	Последовательн сть		{xn}	называется неубывающей (невозрастаю-
О	Последовательн сть		{xn}	называется неубывающей (невозрастаю-
	щей), если каждый последующий член этой последовательности не
	меньше (не больше) предыдущего, т.е. если для всех номеров n									спра-
	ведливо нераве ство xn ≤ xn+1 ( xn ≥ xn+1 ).
	Неубыв ющие и невозрастающие последовательности называются мо-
О
	нотонными последов тельностями.
	нотонными последов тельностями.
	Если вместо нестрогих неравенств xn ≥ xn+1 и xn ≤ xn+1						имеют место стро-
О	Если вместо нестрогих неравенств xn ≥ xn+1 и xn ≤ xn+1						имеют место стро-
	гие неравенства xn < xn+1 или xn > xn+1 , то последовательности называют-

	ся возр ст ющей и убывающей соответственно.
	Скачано

104

Лекции 8 – 9

Пример:

(

)

1). Последовательность {1,1, 2, 2,3,3, 4, 4,..., n, n,...}

- неубывающая.

antigtu

2). Последовательность

– возрастающая, так как xn+1 > xn

2 +1

(n +1)

(n +1)2 n2 +1

− n2

(

(n +1)2 +1

Действительно,

(

n +

)

2 +1

−

n2 +1

((n +1)

+1)(n

+1)

2n +1

> 0 .

((n +1)2 +1)(n2 +1)

3). Последовательность 1

– убывающая, так как

− x =

−

= −

< 0 .

n+1

( +1)

Признак сходимости монотонной последовательности. Если

неубывающая (невозрастающая) последовательность

{xn} ограничена

сверху (снизу), то она сходится.

Докажем, что если неубывающая последовательность ограничена свер-

ху, то она сходится (имеет предел).

Доказательство:

{xn} имеет

{xn}-

ограничена

сверху

x = Sup

= x .

п кажем, что lim x

{ }

n→∞

1) n, xn ≤ x ;

2) ε > 0

айдется элеме т xN > x −ε ,

n > N, xN ≤ xn (по условию {xn}- неубываю-

щая), т.е. з пишем последовательно:

x −ε < xN ≤ xn ≤ x x −ε < xn ≤ x

−x ≤ −xn < −x +ε 0 ≤ x − xn < ε

xn − x

<ε ,

то есть по определению предела x = lim xn .

n→∞

1. Люб я

неубывающая последовательность всегда ограничена снизу

первым элементом.

Любая невозрастающая последовательность всегда

ограничена сверху первым элементом.

2. Не всякая сходящаяся последовательность является монотонной.

Скачано

105

Элементы теории множеств и математической логики. Числовые последовательности

Пример:

{x }

=1+

(−1)k

, lim x

=1, однако {x } - немонотонная.

n→∞

Неограниченная

монотонная

antigtu

бесконечно

последовательность

является

большой.

9.6. Число е как предел монотонной последовательности

Рассмотрим последовательность {x

1 n .

Исходя из признака сходимости монотонной последовательности, доста-

точно доказать, что:

{xn} - является возрастающей;

{xn} - ограничена сверху.

Из 1) и 2) делаем вывод о существовании предела 1+

Доказательство:

Воспользуемся формулой бинома Ньютона:

Скачано

n(n −1)

(a +b)

= anb0 + nan−1b1 +

an−2b2

n(n

−

1)(n

−

n−3 3

(

n −

)(

− 2

)

...

(

−

(

))

0 n

+...... +

a b ,

где n! =1 2 3 ... n .

Тогда

xn =

1 n

=1+ n

n(n

−1) 1

n(n −1)...(n −(n −1)) 1

+...

n −1

2 +

−

+... +

1−

... 1

−

Ан логично для xn+1

xn+1

= 2 +

−

1−

+... +

n +1

e ≈ 2,7 1828 1828 459045...

106 Лекции 8 – 9

	1				1			2			n
+			1	−		1	−		... 1	−		,
	(n +				n +1			n +1			n +1
		1)!

1 − 1

1 −

. Заметим, что

содержит на одно положитель-

n+1

n +1

ное слагаемое больше, чем xn , следовательно n xn < xn+1

Таким образом, {xn} – последовательность возрастающая

При n ≥ 2

<1=> xn > 2 .

0 < 1−

< 2

+... +

; если заменить каждое слагаемое еще боль-

шим:

= 1 ,

,... ,

2 3

2 2

2n−1

2! 2 3!

получаем:

xn < 2 +

+... +

2 −1

{...} - сумма убывающей геометрической прогрессии, для которой

b =

, q =

,b =

S =

b (1 − qn )

S =1−

;

2n−1

1 − q

n S <1 n x <3.

antigtun

Вывод: возрастающая по ледовательность {xn} ограничена сверху, следовательно, последовательность сходится.

		n
	1	с
	1	= e , 2 < e < 3 (Эйлер);
! 1. Обозначение lim 1	+	= e , 2 < e < 3 (Эйлер);
n→∞	n
	n
Скачано

2. Число e имеет большое значение в математическом анализе. y = ex - показатель ая функция с основанием e ;

y = ln x - н тур льный логарифм (логарифм по основанию e ).

3. Спр ведливо утверждение: если {αn} – произвольная бесконечно малая последовательность и αn ≠ 0 , то

lim (1+αn ) 1 αn = e. n →∞

		ru	107
Элементы теории множеств и математической логики. Числовые последовательности			107
9.7. Предельные точки. Верхний и нижний пределы
	.
О Точка x бесконечной прямой называется предельной точкой числовой
последовательности {xn }, если в любой ε -окрестности этой точки име-
antigtu	{ xn }
ется бесконечно много элементов последовательности	{ xn }

! Иногда предельная точка именуется точкой сгущения (что связано с геометрической интерпретацией действительных чисел как точек на числовой оси). Точки, представляющие собой члены последовательности, как бы «сгущаются» вблизи предельной точки.

Подобный «геометрический» подход позволяет высказать два утверждения, строгое доказательство которых опустим:

1) всякая сходящаяся последовательность имеет только одну предельную точку; 2) последовательность, имеющая несколько предельных точек, расходится.

Пример:

1). Последовательность {

1−(−1)

} имеет две предельные точки x = 0 и

x = 2 , но не имеет предела.

2). Последовательность {e−n } имеет одну предельную точку x = 0, кото-

рая является одновременно пределом этой последовательности.

Принцип Больцано – Вейерштра

а. У всякой ограниченной последо-

Скачано

вательности существует хотя бы одна предельная точка.

Наибольшая предельная т чкас

последовательности {xn}

называется

верхним предел м п след вательности и обозначается

lim

x .

n→∞ n

Наименьшая предельная точка

последовательности {xn}

называется

нижним пределом последовательности и обозначается a = lim xn .

n→∞

Пример:

1). Последовательность 1,

1 , 1,

, ..., 1, 1

имеет верхний предел a = 1 и нижний предел a = 0 .

2). Последовательность 1, 2, 3, 1, 2, 4, 1, 2, 5, ..., 1, 2, n, ....

имеет нижний предел a =1 ,

тогда как обычного предела у нее нет, по-

с ольку она неограниченная.

108									Лекции 8 – 9
			Сформулируем без доказательства теорему, показывающую важность
								ru
	этих понятий (значения пределов в ней могут быть и несобственными числа-
	ми, т.е. +∞			или −∞).		antigtu	.
	ми, т.е. +∞			или −∞).
	Т
	Т		Для любой числовой последовательности верхний и нижний пределы
			всегда существуют. Их равенство есть условие, необходимое и доста-
			точное для существования предела (в обычном смысле).
			Предел в обычном смысле также может оказаться несобственным чис-
	!
			лом.
			лом.

			В результате изучения материала, изложенного в этих лекциях,
			студент должен владеть следующими понятиями:
				множество, элемент множества;
				целые, натуральные, рациональные, действительные числа;
			виды числовых множеств (интервал, сегмент, луч и т.п.);
			ограниченные и неограниченные множества;
			числовая последовательность, способы ее задания;
					с
				предел числовой последовательности;
			бесконечно большие и бесконечно малые последовательности,
			их свойства;
				свойства сходящих я по ледовательностей;
				монотонные по ледовательно ти, признак сходимости
		Скачано
				монотонной последовательности;
				предельная точка (точка сгущения) последовательности.

функции. Обсуждаются способы задания функции, различные свойства функций. ru, приводится классификация функций и, для справки, таблица основных элементарных функций с их графиками. Далее рассмотрено опорное для всего математического анализа понятие

Лекции 10 - 11 ФУНКЦИИ. ПРЕДЕЛ ФУНКЦИИ

В лекциях 10 – 11 рассматривается одно из основных понятий математики – понятие

предела функции, приведены разновидности определений (определение по Коши и определение по Гейне, предел в точке и предел в бесконечности, односторонние пределы и т.п.). Заканчивается лекция описанием бесконечно малых и бесконечно больших функций - весьма удобного математического инструмента, широко использующегося в различных доказательствах.

10.1. Понятие функции. График функции. Способы задания функции 10.2. Основные характеристики функции 10.3. Обратная функция. Сложная функция 10.4. Основные элементарные функции

10.5. Элементарные и неэлементарные функции 11.1. Предел функции в точке 11.2. Предел функции в бесконечности 11.3. Односторонние пределы

11.4. Бесконечно малые и бесконечно большие функции и их свойства 11.5. Таблица определений предела

antigtu


	Скачано
10.1. Понятие функции. Графикс				функции.
	Способы задания функции
	Понятие фу кции – од о из основных математических понятий, оно от-
носится к установле ию соответствия между элементами двух множеств.
О	Если задано правило f , по которому каждому элементу x из множества
	X пост влен в соответствие единственный элемент y из множества Y ,
	то говорят, что на множестве X задана функция y = f (x), x X , y Y .
	Множество X		называется областью определения функции (ООФ) и
	обозна ается		D( f ). Множество изменения функции Y называется об-
	л стью зн чений функции (ОЗФ) и обозначается E ( f ).
	В д льнейшем будем рассматривать (в основном) числовые функции,
т.е. фун ции, у		оторых ООФ и ОЗФ Y являются числовыми множествами,
X	, Y .	В этом случае переменная величина x называется независи-

мой переменной или аргументом, величина y - зависимой переменной

или функцией (от x). Число y , соответствующее данному значению x, назы-

вается частным значением функции в точке x.

110

Лекции 10 – 11

Множество точек (x,

f (x))

плоскости Oxy называется графиком функ-

ции y = f (x).

Функция может быть задана: 1) аналитически; 2) графически; 3) с по-

мощью таблицы.

1,antigtux > 0,

При аналитическом задании функция может быть определена:

(x), x D

D( f )

1) явно - уравнением вида y = f (x) или y =

;

(x),

x D D( f )

2) неявно - уравнением вида F (x, y )= 0 ;

3) параметрически – с помощью вспомогательной переменной –

параметра – x = x(t ),

t T

y = y (t ),

Пример:

Явное задание:

{ }

{

}

{ }

{

}

1). y = 1 − x2 ,

x :

≤1 ,

y : 0

≤ y ≤1

;

y =

x ≥ 0,

2).

−x, x < 0,

{x}={x : −∞ ≤ x ≤ ∞},{y}={y : 0 ≤ y ≤ ∞}

3).

y = sgn x - знак x ,

sgn x =

0, x =

Скачано

−1, x < 0,

{x} ={x : −∞ ≤ x ≤ ∞}, {y} ={−1,0,1}

4). Функция Дирихле

y =

0, x −иррац.,

{x} ={x : −∞ ≤ x ≤ ∞},

1, x −рац.,

{y}={0,1}.

5).

y =[x]- цел я часть x

(наибольшее целое,

не превосходящее x )

D ( f )={x} ={x : −∞ ≤ x ≤ ∞},

E ( f )={y} ={y :целыечисла};

эта функция может быть задана в виде

...

[

)

1; 2

[x]

[0;1), .

= 0,

[−1; 0),

−1

...

Функции. Предел функции

111

Неявное задание:

уравнение

F (x, y)= 0

может определять не одну,

а несколько функций вида y = f (x). Так,

уравне-

ние

x2 + y2 −1 = 0

определяет

две

функции:

y = f1 (x)= + 1 − x2 и y = f2 (x)= − 1 − x2 .

Аналитический способ задания функции является наиболее точным и

предпочтительным для дальнейшего исследования функции методами мате-

матического анализа. Графическое и табличное описание возникает, напри-

мер, при исследовании экспериментально наблюдаемых функциональных за-

висимостей, но и в этом случае обычно подбирают подходящую аналитиче-

скую формулу, с достаточной степенью точности воспроизводящую экспе-

риментальные данные (так называемая аппроксимация).

10.2. Основные характеристики функции

Функция f (x)

с симметричной относительно нуля областью определе-

ния X называется четной, если для

любого

x X

выполняется равен-

ство f (x) = f

(

−x).

ледуетantigtu, что ее график симметричен

Из определения четной функции

относительно оси ординат. Например,

функции y

= x2 ,

y = x

являются чет-

ными, их графики имеют вид:

y = x2

y = x

–x0

Функция f (x)

с областью определения

называется нечетной, если

для любого x X

выполняется равенство

f (−x) = − f (x).

Гр фик нечетной функции симметричен относительно начала коорди-

нат.

Н пример, функции y = x3

и y = 2x

являются нечетными, их графики

имеют вид:

Скачано

112

–y0

Лекции 10 – 11

y = x3

y =

–x0

antigtu

Функция y = x2 + x не является

ни четной,

ни

нечетной, так как

(−x)2 + (−x)= x2 − x ≠ ±y .

О Функция y = f (x) называется периодической, если существует такое

число T ≠ 0 , что для любого x X выполнены условия: 1) x +T X ; 2) f (x +T )= f (x). Число T называется периодом функции y = f (x).

Множество значений числовой функции может быть ограниченным, ограниченным сверху (снизу) и неограниченным. В соответствии с этим под-

разделяются и сами функции.
О Функция f называется ограниченной на множестве E D( f ), если
A : x E f (x) ≤ A .
Например, функция y = sin (x) ограничена на всей числовой оси;	y = x	3
	y = x

ограничена на любом промежутке конечной длины, но не ограничена на всей

области определения x .

Функция

называется

граниченнойс

сверху (снизу) на множестве

E D( f ), если A : x E

f (x)≤ A ; ( A : x E

f (x)

≥ A ).

Например, y = x2

огра ичена снизу на всей области определения x .

Точная верх яя (

иж яя) грань множества M значений функции f на

E называется точ ой верхней (нижней) гранью функции f на E и

обозн ч ется sup f (x )

( inf

f (x)).

x E

1 = 0 , inf x2 = 0 .

Например,

sup

x (−∞;0)

Если исло

sup f (x) ( inf

(x)) принадлежит множеству M значений

x E

функции

на E , то оно называется наибольшим (наименьшим) зна-

чением f

на E и обозначается max f (x) ( min f (x)).

x E

Например, min x2 = 0 ,

max

не существует.

x (−∞;0) x

Пусть y = f (x) определена на множестве D( f ) и множество E D( f ).

Скачано

Функции. Предел функции

113

Если x1, x2

E :

x1 < x2

(x1 )< f (x2 )

f (x) возрастающая на E ;

x1 < x2

f (x1 )≤ f (x2 )

f (x) неубывающая на E ;

x1 < x2

f (x1 )> f (x2 )

f (x) убывающая на E ;

x1 < x2

f (x1 )≥ f (x2 )

f (x) невозрастающая на E .

Все четыре типа в совокупности называются монотонными.

на E , а воз-

растающие и убывающие - строго монотонными на E .

10.3. Обратная функция. Сложная функция

Функция y = f (x), x X ,

y Y

обратима, если каждое свое значение

она принимает один раз, то есть для каждого

y Y существует только

одно значение x X такое, что y = f (x).

Тогда

функции

y = f (x),

осуществляющей

y = f (x)

отображение множества X в множество Y,

x = f −1(y)

может быть сопоставлена функция

x = g (y),

осуществляющая отображение Y в X, такое,

что

g ( f (x))= x .

Эта

функция

antigtu

называется

обратной к

f (x)

и обозначает я

f −1 (y).

С другой стороны, для функции

x = f −1 ( y)

обратной является функция

= f (x), поэто-

x = f −1(y)

му функции y = f (x) и x = f

−1

(y) называют-

ся взаимно обрат ыми.

Графики фу кций y = f (x) и x = f −1 (y) сов-

падают,

но

если

мы

хотим

описать

функцию

f −1 (y)

обычным

обр зом,

то

есть

ее

аргумент

y = f −1(x)

обозначить

ерез x , а зависимую переменную че-

рез y , то графическая иллюстрация изменится.

Вначале изменим направления осей; затем

изменим н зв ния осей; в результате получаем,

что гр фики вз имно обратных функций симмет-

Скачано

114

Лекции 10 – 11

ричны относительно биссектрисы первого и

третьего

координатных

углов,

то

есть

линии

−1(x)

y = x .

Множество

значений

обратной функции

y = f −1 (x)

совпадает

областью

antigtu

определения

функции y = f (x), а область определения обрат-

ной функции

y = f −1 (x)

совпадает с множеством

значений функции y = f (x).

Пример:

1) y =

= f (x),

x (− ∞, 0) (0, ∞), y (− ∞, 0) (0, ∞);

g (x)= f −1 (x)

= 1

(обратная функция совпадает

с исходной).

2) y =

f (x)

x > 0, x (− ∞, 0) (0, ∞),

− e x ,

x < 0,

y (−1,0) (1,∞);

x (−1, 0) (1, ∞),

y = f −1 (x)=

ln x, x > 1,

ln(− x), x (−1, 0), y (− ∞,0) (0,∞).

Скачано

одного

переменного,

то функция h ,

Если

фу кции

определен ая

соот ошением

h(x)= g f (x)

на

области

D(h)

{

( f ): f (x)

}

x D

называется сложной функцией или

D(g ) ,

суперпозицией (композицией) функций f и g и обозначается g f .

Операции производятся справа налево – вначале вычисляется частное

значение функции

f и в точке x , а затем для данного числа, рассматривае-

мого к к ргумент, вычисляется значение функции g .

Опер ция суперпозиции может применяться повторно, например,

F (x)= lg

sin (tg (x2 ))

представляет собой суперпозицию пяти операций: воз-

ведение в вадрат, вычисление тангенса, синуса, модуля и логарифма.

Функции. Предел функции

10.4.Основные элементарные функции

1.Степенные функции

				antigtu
	1.1. y = xn , n N .
	1.2. y =	1		, x ≠ 0 .
	1.2. y =		xn	, x ≠ 0 .
			xn
	с

Скачано		y = n x .
	1.3.	y = n x .

1.4. y = xα , α .

115

116

Лекции 10 – 11

2. Трансцендентные функции

2.1. Показательная

2.2. Логарифмическая

y = ax ,

a > 0,

a ≠1.

y = loga x, a > 0,

a ≠1,

x (0,∞) .

antigtu

3. Тригонометрические функции

3.1.

y = sinx

3.2. y

cosx

Скачано

3.4. y = ctgx, x ≠ kπ .

3.3.

y = tg x, x

≠ π + nπ

Функции. Предел функции

117

4. Обратные тригонометрические функции

4.1. y = arcsin x,

| x |≤1.

4.2. y = arccos x, | x |≤1

arcsin(−x) = −arcsin x .

arccos(−x) =π −arccos x

4.3. y = arctg x ,

4.4. y = arcctg x .

arctg(−x) = −arctg x .

arcctg(−x) =π −arcctg x .

antigtu

arcsin x + arccos x = π , arctg x + arcctg x = π , arctg x =

−arctg

1 .

5. Гиперболические функции

5.1. Гиперболический синус

5.2. Гиперболический косинус

y = sh x =

ex −e−x

y = ch x =

ex + e−x

Скачано

118

Лекции 10 – 11

5.3. Гиперболический тангенс

5.4. Гиперболический котангенс

−x

= sh x .

ex + e−x

ch x

y = th x = ex

−e−x

y = cth x = ex −e−x

= sh x .

+ e

ch x

ch2 x −sh2 x =1, th x cth x =1 ,

sh(x + y) = sh xch y +sh y ch x ,

ch(x + y) = ch xch y +sh xsh y .

10.5. Элементарные и неэлементарные функции

Функции, получающиеся из основных элементарных функций и кон-

стант с помощью конечного числа арифметических операций (сложения,

вычитания, умножения, деления) и операций суперпозиции, называются

элементарными функциями.

antigtu

(Список основных элементарных функций, изучаемых в рамках школь-

ного курса математики, пополнен гиперболическими функциями – они

широко встречаются в различныхс

приложениях и тесно связаны с обыч-

ными тригонометрическими функциями.)

y =[x],

Рассмотренные выше функции y = sgn x , y =

функция Ди-

рихле относятся к

еэлеме тарным.

11.1. Предел функции в точке

11.1.1. Число A называется пределом функции y = f (x) в точке a , ес-

ли

для

любой

последовательности

{xn}

такой,

что

xn D( f ), xn

≠ a,

lim xn

= a

, выполняется равенство lim f (x

)= A ,

ко-

n→∞

торое обозн чают:

lim f (x)= A .

Скачано

x→a

Определение 11.1.1 сформулировано «на языке последовательностей»

(иначе определение предела по Гейне).

Функции. Предел функции

119

Пример:

y = x; xn → a y(xn )= xn → a lim x = a.

n→∞

x→a

y = y (x)− функция Дирихле,

x → a, y →?

рациональные−{x }

→ a

{

y (x

)

→1,

}

иррациональные−{x }→ a

{

y (x

) → 0.

n }

Функция Дирихле не имеет предела при x → a , где a - любое.

11.1.2. Число A называется пределом функции y = f (x)

в точке a , ес-

ли ε > 0 δ (ε ) > 0 : x : 0 < x − a < δ (ε ) f (x)− A < ε .

A + e

2ε

A - e

−δ

+δ

Таким образом, для любой ε -

окрестности точки А можно найти δ -

окрестность точки a , такую, что все значения функции для x из δ

- окрест-

ности точки a попадут в ε - окре тно ть точкиantigtuА.

Смысл этого утверждения заключает я в том, что чем ближе точка x

расположена к точке a , тем ближе значение f (x) к числу A .

Определение 11.1.2 сформулировано «на языке эпсилон-дельта» (иначе оп-

ределение предела по К ши).

11.2. Предел фу кции в бесконечности

Если ООФ

е огра иче а сверху (снизу), то можно поставить вопрос о

поведении функции при x →+∞ ( x → −∞).

f (x) при x → +∞ ( x → −∞), ес-

11.2.1. Число A н зыв ется пределом

ли {xn}: xn → +∞ f {xn} → A

{xn}: xn → −∞ f {xn}→ A .

n→∞

Определение 11.2.1 сформулировано «на языке последовательностей».

11.2.2. Число A называется пределом f (x) при x → +∞ ( x → −∞),

если

ε > 0 M (ε ): x : x ≥ M f (x)− A < ε

( ε > 0 M (ε ): x : x ≤ M f (x)− A < ε ).

Скачано

120					Лекции 10 – 11
		Определение 11.2.2 сформулировано «на языке эпсилон-дельта».
		Определение 11.1.1 определение 11.1.2, определение 11.2.1 опре-
	Т
		деление 11.2.2, т.е. определения Гейне и Коши эквивалентны
		деление 11.2.2, т.е. определения Гейне и Коши эквивалентны
		Покажем, как пользоваться обеими разновидностями определений для
		antigtu	.	ru

доказательства существования и отсутствия предела. Для доказательства существования предела обычно удобнее определение Коши, для доказательства отсутствия предела – определение Гейне.

Пример:

y = x2 , x →1. Доказать, что lim x2

=1.

x→1

Доказательство:

ε > 0

x2 −1

< ε,

(x −1)(x +1)

< ε

x −1

x +1

Так как в предельном переходе рассматриваемая область значений x на-

ходится вблизи точки a =1 , можно считать,

что 0 < x < 2 ,

x +1

= x +1 ,

1 < x +1 < 3 ,

<1 , тогда

x −1

< ε , т.е. можно взять δ (ε )=ε . Что-

f (x) при x → a , следует для любо-

бы доказать существование предела

го ε найти формулу для построения δ (ε ).

y =

x +1

, x →∞.

Доказать, что lim

x +1

=1 .

x→∞

Доказательство:

x +1

ε > 0

−1

< ε

, т.е. M (ε )=

y = sin

x → 0 . Доказать, что lim sin

не существует.

x→0

Доказательство:

Р ссмотрим две последовательности

lim xn

= 0 ,

f (xn )= sin (nπ )= 0 ,

lim f (xn )= 0 ;

πn

n→∞

′

+ 2nπ

′

= 0 ,

xn =

π + 4πn

lim xn

f (xn )= sin

=1 , lim f (xn )=1.

n→∞

Поскольку для различных последовательностей значений аргумента,

сходящихся к нулю, соответствующие последовательности значений

функции сходятся к различным пределам,

lim sin

не существует.

Скачано

x→0

Функции. Предел функции

121

11.3. Односторонние пределы

11.3.1. Число A называется правым пределом функции

y = f (x)

если {xn} → a , (xn

> a)

antigtu

точке a ,

{ f

(xn )}→ A . Эквивалентное опре-

деление: число A называется правым пределом функции y = f (x)

точке a ,

если ε > 0 δ (ε ) > 0 : 0 < x − a <δ (ε )

f (x.)− A

< ε .

Обозначение правого предела: lim

f (x ) = A .

x → a +0

11.3.2. Число A называется левым пределом функции y = f (x) в точке

a ,

если

{xn }→ a : (xn < a) {f (xn )}→ A, или

если

ε > 0 ,

то

δ (ε )> 0 : 0 < a − x <δ (ε )

f (x)− A

< ε .

Обозначение левого предела:

lim

(x ) = A .

x → a − 0

Пример:

y = Sgn x , lim Sgn x =1,

lim Sgn x = −1.

x→+0

x→−0

Функция y = f (x) имеет предел в точке a , если правый и левый преде-

Скачано

lim

f (x) = lim f (x) = lim f (x) = A .

лы в точке a существуют и равны:

Доказательство:

x→a+0

x→a−0

x→a

Из определения 11.3.1 ε > 0 δ1 (ε ): 0 < x − a <δ1 (ε )

f (x)− A

< ε .

Из

определения

11.3.2

для

того

же

δ2 (ε ): 0 < a − x < δ2 (ε )

f (x)− A

< ε .

Возьмем

δ (ε )= min{δ1,

δ2},

тогда

можно

сказать,

что

ε > 0 δ (ε ):

x − a

<δ (ε ), то есть lim f

(x)= A .

x→a

11.4. Бесконе но малые и бесконечно большие функции

и их свойства

Фун ция

α (x) называется

бесконечно

малой

в точке

a ,

если

limα (x) = 0 .

x→a

x → +∞

Аналогично определяется функция,

бесконечно малая при

122

( x → −∞).

Скачано

	antigtu	.	ru
с	antigtu
с

Лекции 10 – 11

Функции. Предел функции

123

Свойства бесконечно малых функций:

))

x→a

(

)

x→a

(

)

x→a (

(

)

+ β

(

= 0 .

Если limα

= lim β

= 0 , то lim

Доказательство:

antigtu

xn → a

соответ-

x = 0 ; sin x

- ограниченная функция.

Из условия следует, что для любой последовательности

ствующие последовательности α(xn )→ 0 и β (xn )→ 0 .

Покажем, что α(xn )+ β (xn )→ 0 . Для этого фиксируем произвольное.

ε :

N1 (ε ): n > N1

α(xn )

< ε и

N2 (ε ): n > N2

β (xn )

ε .

Возьмем N = max{N1, N2},

тогда для n > N

α (xn )+ β (xn )

≤

α (xn )

β (xn )

< ε .

Свойство может быть расширено: сумма конечного количества беско-

нечно малых функций есть бесконечно малая функция.

Произведение бесконечно малой функции на ограниченную функцию

есть функция бесконечно малая.

Например,

lim

sin

бесконечно малая функция в точке

= 0.

x→0

Произведение бесконечно малых функций есть функция бесконечно ма-

Скачано

лая.

Если lim f (x)= A ≠ 0, limα (x)с= 0 , то lim

α (x)

= 0.

f (x)

x→a

Функция

f (x) называется

бесконечно

большой в

точке

a , если

M δ (M )> 0 : x : 0 <

x −a

<δ

f (x)

> M . Записывается это как

lim f (x)= ∞. Если же фу кция при x → a не только возрастает по абсо-

x→a

лютной величине, но и сохраняет определенный знак, это обозначают:

lim f (x)= +∞ M δ (M )> 0 : x :

0 <

x − a

<δ f (x)> M ;

x→a

<δ f (x)< M .

lim f (x)= −∞ M δ (M )> 0 : x : 0 <

x − a

x→a

1). Ан логично определяются функции, бесконечно большие при

x → +∞ ( x → −∞ ).

2). Функция, бесконечно большая при x → a , является неограниченной

в о рестности точки a , но обратное утверждение неверно: не всякая не-

ограниченная функция является бесконечно большой.

Так, f

(x)= 1 -

124

> M

Лекции 10 – 11

sin

бесконечно большая при

x →0 , а f2 (x)=

- является неограни-

ченной при x → 0 , но бесконечно большой не является

antigtu

В первом случае для любого числа M

можно указать окрестность

точки x = 0 , в каждой точке которой

(

)

; во втором случае для

любого числа M в каждой окрестности точки x = 0 можно указать

точку, в которой

f (x)

> M , но в этой же окрестности найдутся точки,

не удовлетворяющие

этому условию, для которых, например, f (x)= 0 .

Связь между функциями бесконечно большими и бесконечно малыми

при x → a подтверждается следующей теоремой.

Если α (x) - бесконечно малая функция при x → a и α(x)≠ 0 при x ≠ a ,

то

- бесконечно большая функция при

x → a . Если α(x) - беско-

α(x)

нечно большая, то

- бесконечно малая.

α(x)

Свойства бесконечно больших функций

1˚.

Произведение бесконечно большой функции на ограниченную функцию,

не равную нулю, есть функция бе конечно большая.

2˚.

Скачано

Произведение бесконечно больших функций есть функция бесконечно

большая.

3˚.

Сумма бесконечно б льших функций может не быть бесконечно боль-

шой функцией:

f (x)= x , g (x)=1 − x , f (x)+ g (x)=1.

f (x)

и g (x) - бесконечно боль-

шие при x → ∞ фу кции,

о f (x)+ g (x)

таковой не является;

f (x)= x , g (x)=1 − x2 , f (x)+ g (x)=1 + x − x2 .

Все функции, f (x), g (x) и f (x)+ g (x) -

бесконечно большие при

x → ∞.

11.5. Т блица определений предела

В т блице приведены все встречавшиеся в лекции определения преде-

лов. Для

рат ости приведены только определения Коши.

Функции. Предел функции

125

Понятие

Обозначение

Определение

Предел функции

lim f

(

)

= A

(

)

0 : x : 0

f (x)

ε >

−

< δ

−

< ε

f в точке x = a

x→a

«Обращение

x→a+0

(x)= +∞

antigtu

lim f

(M )

−

<δ

f (x)

функции f

x→a

0 : x : 0

lim f

(x)= −∞

(M )

0 :

x : 0

f (x)

в бесконеч-

−

<δ

ность» в точке

x→a

x = a

lim f

(

)

= ∞

M δ (M )> 0 : x : 0 <

x − a

< δ

f (x)

> M

x→a

Предел функции

lim

(

)

= A

ε > 0

M (ε ): x : x ≥ M

f (x)− A

< ε

f при x → +∞,

x→+∞

соответственно

x→−∞

(

)

= A

ε > 0

M (ε ): x : x ≤ M

f (x)− A

< ε

x → −∞

lim

«Обращение

lim

f (x)= +∞

x0 (M ): x :

x ≥ x0 f (x)> M

функции f

x→+∞

в бесконеч-

lim

f (x)= −∞

x0 (M ): x :

x ≥ x0 f (x)< M

ность» при

x→+∞

lim

(

)

= +∞

)

: x :

x ≤ x f

(

)

> M

x → +∞,

x→−∞

0 (

соответственно

lim

f (x)= −∞

x0 (M ): x :

x ≤ x0 f (x)< M

x → −∞

x→−∞

lim

f (x)= ∞

x0 (M ): x : x ≥ x0

f (x)

> M

x→+∞

lim

f (x)= ∞

x0 (M ): x : x ≤ x0

f (x)

> M

x→−∞

Пределы справа

lim

(

)

= A

ε > 0 δ (ε )> 0 : x : 0 < x − a < δ

f (x)− A

< ε

и слева

x→a−0

(

)

= A

ε > 0 δ (ε )> 0 : x : 0 < a − x < δ f (x)− A < ε

lim

Скачано

δ (M )> 0 : x : 0 < x − a < δ f (x)> M

«Обращение

lim

(x)= +∞

функции f

x→a+0

в бесконеч-

lim

(

)

= +∞

(

)

> 0 : x : 0 < a − x <δ f

(

)

> M

x→a−0

ность» справа и

lim

f (x)= −∞

δ (M )> 0 : x : 0 < x −a <δ f (x)< M

слева

x→a+0

в точке x = a

lim

f (x)= −∞

δ (M )> 0 : x : 0 < a − x < δ f (x)< M

x→a−0

x→a+0

(

)

= ∞

M δ (M )> 0 : x : 0 < x − a < δ f (x) > M

lim

x→a−0

(

)

= ∞

M δ (M )> 0 : x : 0 < a − x < δ f (x) > M

lim

В результате изу ения материала, изложенного в этих лекциях, студент должен вл деть следующими понятиями:

функция, график функции, способы задания функции;предел функции в точке и в бесконечности, односторонние пределы;

бес онечно малые и бесконечно большие функции, их свойства.

Лекции 12-13 ru ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. .

НЕПРЕРЫВНОСТЬ ФУНКЦИЙ

В лекциях 12–13 доказаны основные теоремы, на которые опираются конкретные приемы вычисления пределов функций. Рассмотрены первый и второй замечательные пределы, позволяющие вычислять пределы неопределенных выражений, приведена классификация бесконечно малых величин, показана важность эквивалентных бесконечно малых для вычисления пределов функций. Рассмотрено понятие непрерывности, излагаются определения и теоремы, разъясняющие это понятие.

12.1. Свойства функций, имеющих предел 12.2. Замечательные пределы

12.2.1. Первый замечательный предел 12.2.2. Второй замечательный предел 12.3. Сравнение бесконечно малых функций

13.1. Непрерывность функции

12.1. Свойства фу кций, имеющих предел

Для рассмотрения свойств функций, имеющих предел, будет полезна следующая теорема о связи бесконечно малой функции и функции, имеющей предел. Теоремы этого п р графа сформулированы для пределов в точке x0 ,

но все они справедливы и для пределов при x → ±∞.

Т Если lim f (x) = A и A < ∞, то f (x) = A +α(x), где limα (x) = 0.
	x→x0		x→x0
	x→x0		x→x0
	Док з тельство:
	Если lim f (x) = A, то, по определению Коши, при произвольном ε > 0
	x→x0	f (x)− A		f (x)− A	=α (x).
	выполняется неравенство		< ε . Обозначим
	выполняется неравенство		< ε . Обозначим

Тогда для любого ε > 0 выполняется α (x) < ε . Но это и означает, что α(x) – бесконечно малая при x → x0 .

13.1.1. Непрерывность функции в точке
13.1.2. Непрерывность функции на множестве
13.1.3. Непрерывность основных элементарных функций
13.1.4. Свой тва непрерывных функций
		antigtu
13.1.5. Непрерывно ть обратной функции
13.1.6. Непрерывно ть ложной функции
13.1.7. Свой тва функций, непрерывных на отрезке
13.2. Точки разрыва и их классификация
Скачано	с

126

Лекции 12 – 13

Справедливо и обратное утверждение: если функция f (x) представима

в виде

f (x) = A +α(x), где limα(x) = 0 , то существует lim f (x) = A.

x→x0

Пусть функции y = f (x)

и y = ϕ (x) имеют одну область определения D .

antigtu

Докажем свойство 1:

Если lim f ( x)

= A и

limϕ(x) = B , то

x→x0

lim ( f (x) +ϕ (x)) = lim

f (x) + lim ϕ (x);

x→x0

lim ( f (x) ϕ (x))= lim

f (x) lim ϕ (x);

x→x0

lim (k f (x))= k lim f (x);

x→x0

f (x)

lim f (x)

lim

x→x0

, где ϕ (x) ≠α (x) .

lim ϕ

(x)

x→x0

ϕ (x)

x→x0

Из теоремы о связи функции, предела и бесконечно малой:

lim f (x) = A f (x) = A +α(x),

где limα(x) = 0;

x→x0

lim ϕ (x) = B ϕ (x) = B + β(x),

где

lim β(x)

= 0

x→x0

f (x) + ϕ (x) = (A + α (x))+ (B + β (x))=

Скачано

(A + B)+ (α (x)+ β (x))= (A + B)+γ (x),

где γ (x)=α(x)+ β (x).

Применяя теорему о связи в овь и учитывая, что

lim γ (x) = lim (α(x) + β(x))= 0,

x→x0

получаем

lim

( f (x) +ϕ (x))= A + B = lim f (x) + limϕ (x).

x→x0

Свойства 1, 2, 4, в которых фигурируют три различных предела, можно

читать в двух направлениях: если два любых предела существуют, то

существует и третий и соотношение выполняется.

Замечательные пределы. Непрерывность функции

127

Пример:

Вычислить предел

lim

+ 5

antigtu

− 3

x→2

Значение

функции

(x) =

определено

точке

x = 2 ,

−3

f (2) =

+ 5 =

= 9 , поэтому lim

x2 + 5

22 − 3

x→2

x2 − 3

Если функция f (x) определена в точке x0 , то

lim f (x) = f

l m x

)

= f (x0 ).

x→x0

(x→x0

Пример:

Вычислить предел lim

+ x

− 3x2

x→∞ x3

Как и для последовательностей, применим метод деления числителя и

знаменателя на наивысшую степень x , т.е. на x3 :

x3 + x

∞

1+1 x2

1+ 0

lim

−3x

∞

= lim

−

3 x +1 x

−0 +

=1.

x→∞

Пример:

Скачано

9 +5x + 4x2 −3

Вычислить предел

lim

x→0

Непосредственно п дставляя число x0

= 0 в функцию, получаем неопре-

деленность (0/0). Учтем ф рмулу (a −b)(a + b) = a2

−b2

и умножим чис-

литель и з аме атель

а выражение (

9 +5x + 4x2 +3):

lim

9 +5x +4x2

−3

= lim

(

9 +5x + 4x2 )2 −(3)2

x→0

x→0 x ( 9 +5x +4x2 +3)

= lim

+5x +4x2

−9

= lim

5 +

5 +0

x→0 x ( 9 +5x +4x2 +3)

x→0

9 +5x +4x2 +3

9 +0 +0 +

5 .

128

Лекции 12 – 13

Пример:

Вычислить предел: xlim→+∞ (

x2 +1 − x).

В данном примере имеет место неопределенность типа (∞ - ∞); наличие

иррациональности не допускает прямого сокращения, поэтому применя-

ется следующий прием:

(

)

− g

(

))(

(

)

+ g

(

))

(x)

−

(x)

f (x)− g (x)=

f (x)+ g (x)

f (x)

+ g (x)

lim (

x2 +1 − x) =(∞−∞) = lim

( x2 +1)2 − (x)2

x2 +1 + x

x→+∞

= lim

x2 +1− x2

= lim

= 0

x→+∞

x2 +1 + x

x→+∞ x2 +1 + x

Если функции

y = f (x)

и y =ϕ(x)

имеют одну область определения D

и x D f (x)≤ϕ(x),

то

lim f (x) ≤ limϕ(x). Иначе говоря, знак нера-

x→x0

венства сохраняется при предельном переходе. Заметим, что из строгого

неравенства f

(x)<ϕ

(x) по-прежнему следует lim f (x) ≤ limϕ(x) : пусть

x→x0

f (x)= x4 , ϕ (x)= x2 , при

f (xantigtu)<ϕ(x), но lim f (x) = limϕ(x) = 0 .

Теорема о пределе промежуточной функции.

x→0

Если 1) x D f (x)≤ϕ(x)≤ g (x)

, 2)

lim f (x) = lim g(x) = A ,

то limϕ(x) = A.

x→x0

Скачано

12.2. Замеч тельные пределы. Первый замечательный предел.

Второй з меч тельный предел

В теории пределов большую роль играют два предела, которые, в силу

их важности, полу или названия замечательных пределов.

12.2.1. Первый з мечательный предел

		y = sin x	при x → 0 имеет предел, равный 1: lim sin x		=1.
Т	Фун ция
		x	x→0	x

Замечательные пределы. Непрерывность функции

129

Доказательство:

Рассмотрим единичную окружность.

Пусть COB = x

0 < x <

, OC = OB = r =1 ,

AC = sin x ,

antigtux

OA = cos x , BD

= tg x . Сравнивая

площади треугольника OAC , сектора OBC

и треугольника OBD , получаем

S OAC < SOBC < S OBD ,

1 sin x cos x <

1 x <

sin x .

cos x

Разделим двойное неравенство на sin x (> 0)

: cos x <

. Нера-

sin x

cos x

венство

справедливо

для

x < 0 ,

так

как

cos(−x) = cos x, sin(−x) = sin(x) . Перейдем к пределу при x → 0 :

cos(x)

−x

- функция непрерывная,

cos x →cos(0) =1. Применяя теорему о пределе

промежуточной функции, получаем:

1 ≤ lim sin x ≤

1, то есть lim sin x =1.

x→0

В первом замечательном пределе имеет место неопределенность 0

Скачано

Пример:

Вычислить предел: lim

sin 2x

→0

Если x → 0, то и 2x → 0 и тогда

sin 2x

2 sin 2x

sin 2x

lim

= lim

= 2

lim

= 2 1 = 2.

2 x

x→0

Пример:

Вычислить предел: lim tgx .

→0

lim

tg x

= lim

sin x

= lim

sin x

lim

= 1

= 1.

cos x

cos0

x→0

130

Лекции 12 – 13

12.2.2. Второй замечательный предел

Функция

1 x

y(x)= 1

при x → ∞ имеет предел, равный числу e :

n→∞antigtu

lim 1

= e .

x→∞

Доказательство:

При рассмотрении предела монотонной последовательности было полу-

чено соотношение:

1 n

= e .

lim 1

x →+∞.

n→∞

Пусть

Любое

удовлетворяет

двойному

неравенству

n ≤ x < n +1 ,

где

n =[x]

целая

часть

x .

Тогда

< 1

≤ 1 ,

n +1

1 n

n+1

<1+

≤1

x → +∞

1 +

< 1 +

≤ 1

. При

n +1

n →+∞.

Рассмотрим раздельно пределы левой и правой части двойного неравен-

ства:

lim

n+1

n +1

= e

lim 1

n→∞

Скачано

lim 1

n +1

n→∞

n+1

1 n

= e 1 = e .

lim 1

= lim 1 +

lim 1 +

n→∞

Применяя теорему о пределе промежуточной функции, получаем, что

	+	1 x		+	1 x
e ≤ lim 1	+		≤ e , откуда lim 1	+		= e.
x→+∞		x	x→+∞		x

Пусть x → −∞. Сделаем замену переменной: t = −(x +1),

x = −(t +1);

из x → −∞ следует t → +∞.

1 −t−1

−t−1

t +1 t+1

lim 1

= lim 1−

= lim

x→−∞

t→+∞

t +1

t→+∞ t +1

t→+∞

= lim

1 t+1

= lim

1 t

= e 1

= e

1 +

= lim

lim

t→+∞

Замечательные пределы. Непрерывность функции

131

lim(1+t)1/ t = e

t→0

= 1 ; lim(1+t)1/ t = lim(1+1 x)x

(заменим переменную: t

= e ).

t→0

x→∞

Пример:

Вычислить предел:

lim

1 +1 x

7 x .

x →∞

(

)

lim (1+1 x)

7 x

∞

(1+1 x)

x 7

lim (1

+1 x)

x 7

= lim

= e .

= 1

x→∞

Функция y = ( f (x))ϕ(x)

( f (x)> 0 )

называется

степенно-показательной

функцией или сложно-показательной функцией.

Предел степенно-показательной функции

y = ( f (x))ϕ(x) при x → x0 вы-

числяется по формуле:

lim ϕ ( x)

lim

( f (x))ϕ ( x) = lim f (x) x→x0

x→x

Применим основное логарифмическое тождество, считая

lim f (x) = A,

lim ϕ (x) = B.

x→x0

antigtu

lim (

ϕ ( x )

= lim eϕ

lim ϕ ( x) ln f ( x)

f (x))ϕ ( x) = lim eln( f ( x))

( x) ln f ( x) = ex→x0

x→x0

lim ϕ ( x) lim ln f ( x)

lim f (x)

lim ϕ ( x)

= e

B ln A

= e

ln A

= A

x→x0

x→x

→x

Во втором замечательн м пределе имеет место неопределенность

∞

1 .

Пример:

x +1

2 x−1

Вычислить предел lim

x→∞

x − 2

Вы ислим

предел

lim

x +1

= lim

1 +1 x

1 + 0

предел

1 − 2 x

x →∞ x − 2

x→∞

1 − 0

(2x −1) = ∞. Таким образом, функция

x +1

2 x −1

lim

y =

порождает не-

x →∞

x − 2

определенность [1∞].

x +

x +1

x +1− x +

−1 =1+

=1+

x −

x −2

−2

((x −2) 3)

x −

Скачано

132

x→∞

((x

− 2) 3)

Лекции 12 – 13

x +1 2 x−1

∞

2 x−1

= (1 ) = lim

1 +

lim

x→∞ x − 2

x→∞

((x − 2) 3)

antigtu

x−2

(2 x−1)

= lim

= ex→∞

x−2

= e6 ,

поскольку lim

6x −3

x→∞

x −2

12.3. Сравнение бесконечно малых функций

Пусть функции α1(x) и α2(x) являются бесконечно малыми при x → x0.

Если lim α1(x) = A, то возможно несколько ситуаций:

x→x0 α2 (x)

1) если A < ∞, то α1(x) и α2(x) называются бесконечно малыми одного порядка;

2) если A = 1, то α1(x) и α2(x) называются эквивалентными. Обозначение:

α1(x) α2(x) lim	α1	(x)		=1;
x→x0	α2	(x)
Скачано
3) если A = 0, то функция α1(x) называется бесконечно малой высшего
порядка по сравнению с α2(x).					с	α1(x)
Введем символ α1(x) =			(α2(x)) lim			α1(x)	= 0.
					x→x0	α2 (x)

Т Если α1(x), α2(x), α3(x) являются бесконечно малыми при x → x0 и при

этом α1(x) α2(x), α2(x) α3(x), то lim

α1(x)

= lim

α1(x) .

x→x0

α2 (x)

x→x0

α3 (x)

В самом деле, α3(x) α2(x) lim

α3 (x) =1.

x→x0

α2 (x)

Тогда

lim

α1(x)

= lim

α1(x) α3 (x)

= lim

α1(x)

lim

α3 (x) = lim

α1(x)

1 =

x→x0

α2 (x)

x→x0

α3 (x) α2 (x)

x→x0

α3 (x)

x→x0

α2 (x)

x→x0

α3 (x)

= lim

α1(x) .

x→x0

α3 (x)

Замечательные пределы. Непрерывность функции

133

Аналогично: если α1(x) α2(x) при x → x0, то

lim (

f (x) α1(x)) = lim ( f (x) α2 (x));

x→x0

lim

α1(x)

= lim

α2 (x)

;

x→x0

f (x)

x→x0

f (x)

lim f (α1(x))

= lim f (α2 (x)).

x→x0

Если x → 0, то выполняются следующие эквивалентности:

1) sin x x

5) arcsin x x

9) 1−cos x

2) tg x x

6) arctg x x

10) sh x x

3) ex – 1 x

7) ln(1 + x) x

11)

1± x −1 ±

4) ax −1 x ln a

8) log

(1+ x)

12)

(1 + x)α −1 αx

Указанные эквивалентности

являются

следствиями

соответствующих

предельных соотношений:

antigtu

sin x →1,

−1

= →ln a

x→0

tg x →1,

+ x)

−1

= →a ,

x→0

loga (1+ x) = →

1+ x −1

= →

x→0

ln a

x→0

Пример:

Вы ислить предел lim (1 + sin x)1 x .

x →0

При x → 0 применим sinx x.

lim (1 + sin x)1 x

= lim

(1 + x)1 x = e.

x →0

Пример:

Вычислить lim

ln(1 + sin x)

x→0

sin 4x

При x → 0 применим эквивалентность sinx x, sin4x 4x.

Скачано

134

Лекции 12 – 13

lim ln(1 + sin x)

= lim ln(1 + x)

1 lim ln(1 + x) =

1 =

1 .

x→0

sin 4x

→0

4 x→0

Пример:

Вычислить lim 1 + cosπ x .

→1

tg2π x

Заменим t = x - 1. Получаем t → 0 и x = t + 1, тогда cos.πx = cosπ(t + 1) =

= cos (πt + π) = -cosπt, tg2πx = tg2π(t + 1) =

g2(π + π) = g2πt.

2 sin2 π

πt 2

+ cosπ x

− cosπt

lim

= lim

= 2 lim

2 2 =

= lim

x→1

π x

t →0

πt

t →0

tg πt

t →0

(πt)

= 2 lim

π 2t2

= 2 lim

π 2t2

t →0

4 2

13.1. Непрерывность функции

13.1.1. Непрерывность функции в точке

Пусть функция

y = f (x)

определена на множестве

D и пусть точка

x0 D . Функция

y = f (x)

называется непрерывной в точке x0 , если

функция определена в точке x0 ,

antigtu

уществует предел lim f (x) и при этом

x→x0

lim f (x) = f (x0 ). (Иначе: 1) f (x0 ) , 2) lim f (x) , 3) lim f (x) = f (x0 ) ).

x→x0

1).

При нарушении люб го из трех условий функция называется раз-

рывной в точке x0 .

2).

Поскольку

lim x = x0 ,

поэтому первое определение непрерывности

x→x0

)

может быть записа о в виде lim f (x) = f

lim(x)

, то есть операция вы-

x→x0

(x→x0

числения непрерывной в точке x0

функции

y = f (x)

и операция вычис-

ления предела перест новочны.

Пример:

f (x) = x ,

lim f (x) = lim x = x

= f (x ) .

0 x

→x

x→x

f (x) = x

- непрерывна в любой точке

x0 по опре-

делению.

2) f (x) =

, x

< 0,

1, x ≥ 0.

f (x) непрерывна в любой точкеx0

≠ 0 ,

Скачано

Замечательные пределы. Непрерывность функции

135

f (x) разрывна в точке 0 (нарушено второе условие определения).

Рассмотрим точку x0 D функции y = f (x) и точку x ≠ x0

Величина ∆x = x − x0

называется приращением аргумента, x = x0 +∆x .

Величина

∆ y = f (x0 + ∆x)− f (x0 ) называется приращением функции, со-

ответствующим данному приращению аргумента ∆x .

Функция y = f (x)

называется непрерывной в точке x0 ,

если функция

определена в точке x0 и при этом lim ∆y = 0.

∆x→0

Вариант формулировки: функция непрерывна в точке, если беско-

нечно малым приращениям аргумента соответствуют бесконечно

малые приращения функции.

Пример:

Показать, что первое и второе определения непрерывности равносильны.

Используя арифметические свойства предела, получаем

lim ∆y = 0, lim [ f (x0 + ∆x) − f (x0 )]= 0,

∆x→0

lim

f (x0

+ ∆x) − lim

f (x0 ) = 0, lim

f (x0 + ∆x) − f (x0 ) = 0.

∆x→0

∆x

→0

∆x→0

По определению приращения ∆x = x − x0 , поэтому

lim

f (x0 + ∆x) = lim f (x),

∆x→0

x→х

antigtu0

и тем самым lim

f (x) − f (x0 ) = 0

или lim

f (x) = f (x0 ).

x→x0

Функция y = f (x)

если функция

называется

непрерывной в точке x0 ,

определена

т чке

x0 ,

существуют

односторонние пределы

lim

f (x),

lim

f (x) и при этом

lim

f (x) = lim f (x) = f (x0 ) .

x→x0 −0

x→x0 +0

x→x0 −0

x→x0 +0

Все три определе ия

епрерывности равносильны.

Используется т кже понятие односторонней непрерывности.

Функция y = f (x)

н зывается непрерывной в точке x0 слева,

если

функция определена в точке

и существует односторонний предел

lim

f (x) и при этом lim f (x) = f (x0 ) .

x→x0 −0

Функция y = f (x)

называется непрерывной в точке x0

справа,

если

функция определена в точке

и существует односторонний предел

lim

lim f (x) = f (x

)

f (x) и при этом x→x +0

x→x +0

Скачано

136					Лекции 12 – 13
		Используя понятие односторонней непрерывности, можно сказать, что
	!
		функция непрерывна в точке x0 , если она непрерывна в ней справа
		и слева.		ru
	13.1.2. Непрерывность функций на множестве
		Функция, непрерывная в любой точке множества
	О
	О		D , называется не-
		прерывной на множестве D .	.
			.

		Для некоторых точек множества двусторонние пределы могут не суще-
		ствовать, например, если в качестве множества D рассматривается отре-
		зок [a,b]. В этом случае в крайних точках отрезка двусторонние преде-
		лы заменяются на односторонние.

О Функция непрерывна на отрезке [a,b], если она непрерывна на интервале (a,b), непрерывна справа в точке a и непрерывна слева в

13.1.3. Непрерывность основных элементарных функций

Основными элементарными функциями обычно называют следующие:

точке b .	antigtu

y = xα , ax , loga x , sin x , cos x , tg x ,				ctg x,		rcsin x , arccos x , arctg x , arcctg x.
	Основные элементарные функции непрерывны в каждой точке x0								их об-
Т	Основные элементарные функции непрерывны в каждой точке x0								их об-
	ласти определения.
Скачано
Пример:
		с
		Показать, что функция y = x2 непрерывна в произвольной точке x							веще-
								0
		ственн й си.
		∆y = (x0 + ∆x)2 – x02 = x02 + 2x0 ∆x + ∆x2 – x02 = 2x0 ∆x + ∆x2.
		lim ∆y = lim (2x0 ∆x + ∆x2 )			= 2x0	lim ∆x + lim ∆x lim ∆x = 2x0 0 + 0 0 = 0.
		∆x→0	∆x→0			∆x→0		∆x→0 ∆x→0
					в произвольной точке x0 вещественной
!	Непрерывность функции y = xn				в произвольной точке x0 вещественной
	оси док зыв ется с использованием формулы бинома Ньютона.
Пример:
Пример:
		Пок зать, что функция f (x) = sin x					непрерывна в произвольной точке x0
		вещественной оси.
		Док жем, что:
		1)	lim sin x = 0 . {xn } → +0				(x > 0) .
			x→+0
		По лемме 0 < sin xn < xn		при n → ∞ , по теореме о переходе к пределу в
		неравенствах lim sin xn = 0 . lim sin x = 0 = sin(0) - непрерывность в
			n→∞		x→0+

Замечательные пределы. Непрерывность функции

137

точке x = 0 справа. Пусть {xn} → −0 . Заменим x на (−x), (−x) > 0 .

Тогда выполняется условие: 0 < sin(−x) < (−x) , 0

< −sin x < (−x) .

Умножим

неравенство

на

(-1).

Тогда

0 > sin x > x .

Рассмотрим

(xn < 0) ,

xn < sin xn < 0

lim sin x = 0 = sin(0) -

непрерывность в

2antigtu

точке x =0 слева.

x→0−

2) точки x = x0 ≠ 0 .

Покажем,

что

lim sin x = sin x0

то есть

lim(sin x − sin x0 ) = 0 .

x→x0

sin x −sin x

= 2 cos

x + x0

sin

x − x0

lim (sin x −sin x0 ) = 2 lim (cos

x + x0

s n

x − x0

) = 0

(так

как

cos

x + x0

x→x0

величина ограниченная,

sin

x − x0

- бесконечно малая и →0 ) и все

произведение →0 .

Пример:

Вычислить предел: lim sin x.

x→π

Функция y = sinx непрерывна в любой точке, поэтому

lim sin x = sin lim x

= sin

x→π

Скачано

13.1.4. Свойства непрерывных функций

Если функции y = f (x)

и y =ϕ(x)

определены на множестве D и

непрерывны в точке x0 D , то функции

f (x)

f (x)+ϕ(x), k f (x), f (x) ϕ (x),

ϕ(x)

непрерывны в то ке x0 , причем частное требует условия ϕ(x0 )≠ 0 .

Поскольку функции непрерывны в точке x0 , выполняется условие:

lim f (x) = f (x0 ), limϕ (x) =ϕ (x0 ).

x→x0

Используя рифметические свойства предела, получаем:

lim ( f (x) +ϕ (x))= lim f (x) + limϕ (x) = f (x0 ) +ϕ (x0 ),

x→x0

но это и означает, что функция

f (x)+ϕ(x)

непрерывна в точке x0 .

138

Лекции 12 – 13

1). Многочлен Pn(x) = anxn + … +a1x + a0 непрерывен в любой точке

вещественной оси.

a xn

P (x)

+... + a x + a

2). Дробно-рациональная функция

R(x) =

не-

antigtu

+ + b x + b

Q (x)

b xm

прерывна в любой точке x0

вещественной оси, где Qm(x0) ≠ 0

Если функция y = f (x)

непрерывна в точке x0 , то она ограничена в не-

которой окрестности этой точки.

Об устойчивости знака непрерывных функций.

Если f (x)

- непрерывна

в точке

f (x0 ) ≠ 0 ,

то такая δ -

окрестность

точки x0 ,

что для всех

значений

из этой окрестности

f (x) ≠ 0 и имеет знак, совпадающий со знаком f (x0 ) .

Доказательство:

По условию, lim f (x) = f (x0 ) .

x→x0

Таким образом, ε > 0 δ :

x − x0

<δ

f (x) − f (x0 )

< ε ,

то есть, f (x0 ) −ε < f (x) < f (x0 ) +ε .

f (x0 ) −ε ,

f (x0 ) +ε

и f (x0 ) должны

Если взять ε : ε <

f (x0 )

, то числа

иметь одинаковый знак. Таким образом, для ε <

f (x0 )

, f (x) из ε - окре-

стности имеет один знак с

f (x0 ) .

Скачано

13.1.5. Непрерывность обратной функции

Если:

1) y = f (x) - стр го м н т нная, непрерывная на [a,b],

2) α = f (a),

β = f (b) , то x = f −1 ( y)

- строго монотонная, непрерывная

на [α, β].

Пример:

y = sin x ,

на −

, π

строго монотонна и непре-

рывна имеет строго монотонную и непрерывную

обратную функцию x = arcsin y на [−1,1].

После переобозначения y = arcsin x .

13.1.6. Непрерывность сложной функции

Фун ции, полученные в результате суперпозиции двух или большего

числа функций, называются сложными:

Замечательные пределы. Непрерывность функции				.	ru	139
Замечательные пределы. Непрерывность функции						139
	Пусть: 1) x =ϕ(t) задана на {t} и имеет	множество		значений		{x};
О	Пусть: 1) x =ϕ(t) задана на {t} и имеет	множество		значений		{x};
	2) y = f (x) задана на {x}.
	2) y = f (x) задана на {x}.
	Тогда на {t} задана сложная функция	y = f (x) ,	где		x =ϕ(t)	или
	y = F(t) = f [ϕ(t)], x - промежуточный аргумент, t -		независимая пере-

менная.

Пример:

y =sin x , x = t2 , y = sin t2 - сложная функция.

ТНепрерывность сложной функции.

но

f (x ) = f ϕ(t

)

, то е ть

→ a

,antigtuf ϕ(t ) → f ϕ(a) f ϕ(t) -

Если: 1)

=ϕ(t)

непрерывна в точке

= a ,

y = f (x) непрерывна в точке x = b =ϕ(a) ,

то y = f [ϕ(t)] непрерывна в точке

= a .

Доказательство:

Используя определение предела по Гейне, докажем, что

lim f [ϕ(t)]

= f [ϕ(

)]

= f (b) .

{ n}

{

}

t→a

→ a

→ϕ(a) = b (доказано условие 1)),

ϕ(t

)

xn =ϕ(tn ) , то есть {xn} →b , { f (xn )} → f (b)

(доказано условие 2)),

[

n ]

{ n}

{ [

n ]}

[

]

[

]

непрерывна в точке t = a , что и требовалось доказать.

Скачано

то в результате их сложения,

1). Если исходные функции непрерывны,

вычитания, умножения, деленияс

(если знаменатель ≠ 0 ), взятия обратной

и сложной функций п лучаются непрерывные функции.

2).

Для

непрерывн й в

т чке

функции

f (x)

справедливо:

lim f (x) = f (x0 ) = f (lim x) .

x→x0

Для непрерыв ых фу кций переходить к пределу можно под знаком

функций:

а)

lim ex

lim x

= ex→5

= e25 ,

x→5

б) lim ln(1 + sin x) = ln(lim(1 + sin x)) = ln(1 + 0) = 0 .

x→0

140

Лекции 12 – 13

13.1.7. Свойства функций, непрерывных на отрезке

Если f (x)

непрерывна

на

[a,b],

то она

ограничена

на

этом

отрезке

( M и m : m ≤ f (x) ≤ M x [a,b]).

Пример:

antigtu

f (x) = sin x, 0,

m = −1, m = −5, m = 0,

M = 2,

M = 3,

M =1,

m = inf

{f (x)}= 0, M = sup{f (x)}=1,

Требование непрерывности на отрезке является обязательным,

так как

функция, непрерывная на интервале, может и не быть ограниченной.

Пример:

f (x) = 1

непрерывна на интервале (0, 1), то есть

f (x) - не ограничена.

x , 0 < x <1.

Скачано

[a,b], то она достигает на нем своих точной

Если f (x)

непрерывна на

верхней и точной нижней граней

, x2 [a, b]: f (x2 ) = m ).

( x1 [a, b]: f (x1 ) = M

Доказательство:

ет точки x1

От против ого: если

f (x) < M

f (x) − M

< 0 или

− f (x) > 0 .

Рассмотрим F(x) =

, F(x) - непрерывна на [a,b]

(по теореме о

− f (x)

непрерывности сложной функции).

Из непрерывности F(x) следует ее ограниченность на [a,b],

F(x) =

≤ B f (x) ≤ M

−

M − f

(x)

−

- неточная верхняя грань. Полученное

- верхняя грань, тогда M

противоречие доказывает теорему.

Замечательные пределы. Непрерывность функции

141

Пример:

= 0,

M = f (

) =1

f (x) = sin x , x 0,

m = f (0)

, x [−1,1].

antigtu

f (x) =

m = 0, M

1 .

1). Для интервалов (a,b)

и полуинтервалов [a,b)

или (a,b]

теорема не

справедлива.

Пример:

y = x,

(0,1) .

Значения m = 0 и M

=1 - не достигаются на x (0,1) .

2). Для f (x) ,

непрерывной на [a,b],

можно назвать наимень-

m и M

шим и наибольшим значениями функции:

,min f (x) = m.

max f (x) = M

[

]

Если функция y =

f (x) непрерывна на

a,b

и имеет на концах отрезка

значения f (a)

f (b) разных знаков,

то найдется точка ξ (a,b) такая,

что f (ξ) = 0.

Скачано

Доказательство:

{x}: f (x) < 0 , {x}

Пусть f (a) < 0, f (b) > 0 . Рассм трим

ограничено

сверху, например, числ м b sup{x} =ξ . Покажем, что

f (ξ) = 0.

Если бы f (ξ) = C > 0 , тогда по теореме о сохранении знака непрерывной

функции

существовала

бы

δ -окрестность

точки

ξ : x (ξ −δ,ξ +δ) f (x) > 0 ,

но тогда бы ξ не являлась бы точной

верхней гр нью sup{x}, где

f (x) < 0 . Аналогично для f (ξ) = C < 0 оста-

ется f (ξ) = 0, что и требовалось доказать.

Теорема о прохождении непрерывной функции через любое промежу-

точное зна ение. Если функция y= f (x) - непрерывна на [a,b], имеет на

конц х отрезка значения f (a) = A, f (b) = B и число С расположено меж-

ду числ ми А и В : A < C < B ,

то найдется точка ξ (a,b)

такая, что

f (ξ) = C .

142

Лекции 12 – 13

Доказательство:

Рассмотрим:

C : A < C < B, F(x) = f (x) −C F(a) <

0, F(b) > 0. F(x) -

непрерывна

на

[a,b]. По

предыдущей теореме

ξ (a,b) ,

F(ξ) = 0 f (ξ) −C = 0 f (ξ) =C

antigtu

, что и требовалось доказать

Теорема применяется для отыскания корней уравнения вида F(x) = 0

методом половинного деления отрезка.

Пример:

Имеет ли корень уравнение sinx – x + 1 = 0?

Рассмотрим функцию f(x) = sinx – x + 1, которая непрерывна на всей чи-

словой оси, поскольку является суммой непрерывных функций.

f(0) =1>0, f(2π) = -2π + 1 < 0. Следовательно, внутри отрезка [0, 2π] име-

ется, по крайней мере, один корень исходного уравнения.

Пример:

Принимает ли функция

f (x) =

−si π x +

3 значение 2

внутри отрез-

ка [-2, 2]?

Функция является непрерывной на [-2, 2]. На концах отрезка функция

принимает числовые значения f(-2) = 1, f(2) = 5.

Так как 1 < 2 3 < 5, то ξ (-2, 2) такая, что

f (ξ) = 2

3 .

Скачано

13.2. Точки разрыва и их классификация

Точка x0, в которой функция y = f(x) обладает свойством непрерывности,

называется точкой

епрерывности функции, в противоположном случае

точка x0 называется точкой разрыва функции.

Для кл ссифик ции точек разрыва удобно использовать третье опреде-

ление непрерывности.

Если

односторонние

пределы

существуют,

причем

lim

f (x) =

lim

f (x), а функция y = f(x) не определена в точке x0, или

x→x0 −0

x→x0 +0

lim f (x) ≠ f (x0 ), то точка x0 называется точкой устранимого разрыва.

x→x0

Устр нимый разрыв можно устранить, вводя функцию

f (x),

x ≠ x ,

(x) = lim

f (x),

x = x .

→x

Замечательные пределы. Непрерывность функции

143

Пример:

−4

, x ≠ 2,

f (x) =

−2

x = 2.

Точка x = 2 - точка устранимого разрыва, посколь-

ку lim

f (x) =

lim f (x) = 4 ,

≠ 4 .

f (2) = 5

x→2+0

x→2−0

−4

, x ≠ 2,

Устраним разрыв:

f1 (x) = x −2

x = 2.

Функция

f1 (x) непрерывна всюду.

Если: 1) x0 – точка разрыва

f (x) ,

2) существуют конечные пределы справа и слева:

lim

f (x), lim

f (x) ,

x→x0

x→x0 −0

3) lim

f (x) ≠

lim

f (x),

antigtu

x→x0 +0

x→x0 −0

то точка x0 называется точкой разрыва 1-го рода (неустранимый ко-

нечный скачок).

Пример:

y = f (x) =

1 1 , x = 0 - т чка разрыва

f (x) .

1+ 2x

x → +0,

x → −0,

lim

1 1

1 → +∞,

= 0 .

lim

= 1

→ −∞,

=1.

x→0+0

x→0−0

+ 2x

1+ 2 x

2 x → +∞.

2 x

→ 0.

x = 0 - то ка разрыва первого рода.

Если хотя бы один из односторонних пределов не существует или бес-

конечен, то точка х0

называется точкой разрыва 2-го рода.

Скачано

144										Лекции 12 – 13
Пример:
		f (x)	=	1	, x = 0 -	точка разрыва 2-го рода; так
				x	f (x) = +∞ ,		f (x) = −∞		ru
		как lim			f (x) = +∞ ,	lim	f (x) = −∞
	0	x	→0+			x→0−		.
	0	.
		.

В результате изучения материала, изложенного в этих лекциях,
студент должен знать:
методы практического вычисления пределов;
	замечательные пределы;
	эквивалентные бесконечно малые;
	различные определения непрерывности;
	свойства непрерывных функций;			antigtu
	классификацию точек разрыва.
Скачано		с
		с

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ

antigtu	в окрест-
Целью этого раздела является исследование поведения функции y = y( x)	в окрест-
ности точки x по ее числовым характеристикам в самой этой точке

Лекции 14 - 15 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

В лекциях 14 – 15 излагаются основные понятия дифференциального исчисления – понятия производной и дифференциала, рассматривается их геометрический и механический смысл. Выведены правила и формулы дифференцирования, указаны методы вычисления производных для различных способов задания функций. Показано практическое применение дифференциала в приближенных вычислениях.

14.1. Производная функции.

14.1.1. Определение производной функции 14.1.2. Геометрический смысл производной.

Уравнения касательной и нормали к графику функции 14.1.3. Механиче кий мы л производной

14.2. Правила и формулы дифференцирования
Скачано
14.2.1. Производная суммы, разности,
произведения и частного функций
14.2.2. Пр изв дная братнс	й функции

14.2.3. Таблица пр изв дных 14.2.4. Пр изв дная сл жн й функции

14.2.5. Логарифмическая производная 14.2.6. Производ ая еявной функции

14.2.7. Производ ая функции, заданной параметрически 15.1. Производные высших порядков

15.1.1. Определение производной n-го порядка 15.1.2. Пр вила вычисления производной n-го порядка 15.1.3. Вторая производная от неявной функции

15.1.4. Вторая производная от параметрически заданной функции 15.1.5. Механический смысл второй производной

15.2. Дифференциал функции 15.2.1. Дифференциал независимой переменной

15.2.2. Свойства дифференциалов 15.2.3. Геометрический смысл дифференциала

15.2.4. Применение дифференциала к приближенным вычислениям 15.2.5. Дифференциал сложной функции 15.2.6. Дифференциалы высших порядков

146

Лекции 14 – 15

14.1. Производная функции

14.1.1. Определение производной функции

Пусть y = f (x)

определена на (a,b)

x (a,b)

- некоторая фиксирован-

antigtu

ная точка, ∆x - приращение аргумента в точке

x ,

∆y = f (x + ∆x) − f (x) - со-

ответствующее приращение функции,

∆y

- отношение приращений (зависит

от ∆x , x - фиксировано).

∆x

Производной функции

f (x)

в точке x называется

lim

∆y

при условии,

∆x→0

∆x

что он существует. Обозначение:

y′ = dy

= lim

∆y = lim

f (x + ∆x) − f (x)

∆x→0

∆x

∆x→0

∆x

Функция f (x)

называется дифференцируемой в точке x , если произ-

′

водная y (x) существует; операция нахождения производной называется

дифференцированием.

Функция f (x) называется дифференцируемой на интервале (a,b), ес-

ли она дифференцируема в каждой точке этого интервала.

Найдем, исходя из определения, производные некоторых элементарных

функций.

Пример:

Скачано

y = sin x,

y′ = ?

∆x

′

sin(x + ∆x) −sin x

2 cos x +

sin

y (x) = lim

∆x

= lim

∆x

→0

∆x

→0

∆x

sin

∆x

sin ∆x

cos x +

= lim

= cos x, т.к. lim

=1 .

∆x→0

∆x

∆x→0

∆x

′

(sin x) = cos x .

Пример:

y(x) = loga x,

′

0 < a ≠1, y (x) = ?

x +∆x

∆x

∆y = loga (x +∆x) −loga x = loga

= loga 1

∆x

loga 1+

∆x

y′ = lim

∆x

= lim loga 1+

∆x

∆x→0

Производная и дифференциал

147

∆x

x x

∆x

loga e .

= loga lim

= loga

lim

= loga ex

∆x→0

′

loga e ,

′

antigtu

(loga x)

(ln x)

Пример:

y = xα ;

y′ =

xα

′

= lim

(x + ∆x)α − xα

(

)

∆x

∆x→0

Без ограничения общности можем считать α натуральным показателем и

раскрыть скобку, как бином Ньютона:

lim (x + ∆x)α − xα

= lim

xα + α xα−1 ∆x +α (α −1)xα−2 ∆x2

+ ... − xα

∆x

∆x→0

∆x

∆x→0

= lim

α xα−1 ∆x + α (α

−1)xα−2 ∆x2

... = lim

α xα−1

+ o(∆x) =α xα−1 .

∆x

{

}

∆x→0

14.1.2. Геометрический смысл производной. Уравнения касательной

и нормали к графику функции

Рассмотрим две точки графика функции

Скачано

f (x) : M (x, f (x))

P(x

+ ∆x, f (x + ∆x)) . MP -

секущая.

При стремлении ∆x к нулю

(т.е.

при

стремлении точки P к т чке M ) эта секущая

будет поворачиваться от

осительно точки M .

Касательной

графику

функции

y = f (x) в точке

M (x, f (x))

называется предельное положение секу-

щей при ∆x → 0 ( P → M ).

Нормалью к графику функции y = f (x)

в точке M (x, f (x))

называется

перпендикуляр к касательной, проведенный через точку касания.

Если функция

y = f (x)

имеет в точке x

производную

′

(x) , то график

функции в точке M (x, f (x))

имеет касательную с угловым коэффициен-

′

том f (x) .

148

Лекции 14 – 15

Доказательство:

′

ϕ(∆x) = ∆y

∆x →0 .

Так

существует

Пусть

как

∆y

∆x

antigtu

′

lim

∆x

= f (x) = lim tgϕ(∆x) ,

то:

1) существует предельное положение

∆x→0

секущей, то есть касательная; 2) угловой коэффициент касательнойru

ра-

вен f (x) .

1). Значение

y′(x0 ) позволяет записать уравнение касательной к кри-

вой y = y(x)

в точке x0 :

y − y0 = y′(x0 ) (x − x0 ).

2). Поскольку условие перпендикулярности прямых:

k1 k2 = −1,

то

уравнение нормали имеет вид:

y = f (x0 ) +

−1

(x − x0 ) .

f ′(x0 )

3). При

y′(x)> 0 в точке

функция является возрастающей, а при

y′(x)< 0 – убывающей.

14.1.3. Механический смы л производной

Рассмотрим движение точки по прямой. S = f (t)

- перемещение точки в

Скачано

′

f (t + ∆t) − f (t)

момент времени

t , V = f (t) = lim

∆t

- мгновенная скорость в

момент времени t .

∆t→0

Пример:

S (t )=

gt2

, V (t) =S '(t )= gt .

14.2. Пр вила и формулы дифференцирования

14.2.1. Производная суммы, разности, произведения и частного функций

1)	(c)′ = 0 , c = const ;
2)					′	′		′
2)	( f (x) ± g(x))					= f (x) ± g (x) ;
3)				′		′
3)	(c f (x)) = c					f (x) ;
4)					′	′		′
4)	( f (x) g(x)) = f (x)							g(x) + g (x) f (x) ;
		f (x)	′		′			′
5)		f (x)		=	f (x)g(x) − g (x) f (x)				.
5)		g(x)		=		g	2	(x)	.
		g(x)				g		(x)

Производная и дифференциал

149

Доказательство правила 2:

lim ( f + ∆f )+(g + ∆g )−( f + g )

∆x→0

∆x

= lim

f + ∆f − f

+ lim

g +∆g − g

∆x→0

∆x

∆x→0

∆x

= lim

∆f

+ lim

∆g = f

+ g

∆x→0

∆x

∆x→0

∆x

Пример:

′

y = 3sin x +5log2 x −10 ,

= 3cos x +5 x log2 e .

14.2.2. Производная обратной функции

Пусть f (x)

1) строго монотонна и непрерывна в окрестности точки x0 ,

2) функция дифференцируема в точке x0 и

f ′(x0 ) ≠ 0 ,

тогда:

antigtu

: (f −1( y))′;

1) существует производная обратной функции в точке x0

2) (f −1( y))′y=y0 =

f ′(x0 )

Доказательство:

Из условия 1 следует существ вание непрерывной строго монотонной

обратной фу кции x = f −1 ( y) .

Рассмотрим x = f −1 ( y)

в окрестности

точки y0 = f (x0 ) . Зададим приращение аргументу ∆y ; ему соответствует

приращение функции ∆x и ∆x

(*).

∆y

∆x

Из строгой монотонности

f −1 ( y) при ∆y ≠ 0 следует, что ∆x ≠ 0 . Устре-

мим ∆y →0 , из непрерывности

x = f −1 ( y) ∆x → 0 .

Но при ∆x → 0 ,

∆y → f ′(x0 ) , следовательно,

∆x

→

∆y

f ′(x0 )

∆x

Та им образом,

(f −1( y))′y=y0 =

f ′(x0 )

Скачано

150

Лекции 14 – 15

Пользуясь этой формулой, найдем производные некоторых элементар-

ных функций.

1) y = ax ,

(ax )′ = ?

a > 0, a ≠ 0

. x = loga y ;

′

)

= a

ln a ;

′

loga e

(loga y)

loga e

(ax )′ = ax ln a , (ex )′ = ex .

2)y = arcsin x , (arcsin x)′ = ? x = sin y ,

(arctg x)′ =

= cos2 y =

=antigtu1 ;

(arcsin x)′ =

;

(sin y)′

cos y

1 −sin2 y

1 − x2

(arcsin x)′ =

1 − x2

3) (arccos x)′ = −

1 − x2

4) y = arctg x, (arctg x)′ = ?

x = tg y

, (tg y)′ =

;

cos2 y

(tg y)′

1 + tg2 y 1 + x2

Скачано

(arctg x)′ =

1+ x2

5) (arcctg x)′ = −1+1x2 .

14.2.3. Таблица производ ых

Таблица получена, исходя из определения производной и правил дифференцирования.

1.	(xα )′ =α xα−1 .
2.	(ax )′ = ax ln a (a > 0, a ≠1) (ex )′ = ex .
3.	(loga x)′ = loga e	1	(a > 0,a ≠1) (ln x)′	=	1 .
	(sin x)′ = cos x .	x			x
4.	(sin x)′ = cos x .
5.	(cos x)′ = −sin x .

		1				− x2					ru	151
Производная и дифференциал
	′	1								.
6.	(tgx) =		cos2 x		.
	′	1
7.	(ctgx)	= −					.
				sin2 x
8.	(arcsin x)′ =					1		.

9.	(arccos x)′ = −					1			.

						1 − x2

10.(arctgx)′ = 1 +1x2 .

11.(arcctgx)′ = −1 +1x2 .

sh2 x

antigtu

shx

12.

(shx)′

= chx .

Гиперболический синус shx =

ex −e−x

13.

(chx)′ = shx .

Гиперболический косинус chx =

ex + e−x

′

shx

14.

(thx)

Гиперболический тангенс thx = chx .

ch2 x

(cthx)′ =

chx

15.

Гиперболический котангенс cthx =

Скачано

14.2.4. Производная сложной функции

Если:

y = f [ϕ(t)]

- сл жная функция, t- независимая переменная,

ϕ -

промежуточный

аргумент;

2) существуют

f ′(x )

и ϕ′(t0 ) , где

x0 =ϕ(t0 ) , то {f [ϕ(t)]}′ = f ′(x0 ) ϕ′(t0 ) .

Док з тельство:

Рассмотрим:

t0 +∆t ∆x =ϕ(t0 +∆t) −ϕ(t0 ) , ∆x ∆y = f (x0 +∆x) − f (x0 ).

Пусть ∆t →0 , тогда lim

∆x

(см. условие f ′(x0 ) = y′(x0 ) ).

Вычислим:

∆t→0

∆t

lim

∆y

= lim

∆y

∆x = lim

∆y

lim

∆x = f ′(x0 ) ϕ′(t0 ) ,

что

и требовалось

∆t→0

∆t

∆t→0

∆x

∆t

∆t→0

∆x

∆t→0

∆t

до азать.

Независимой переменной была t , промежуточным аргументом -

x . На

практике чаще имеем дело с функциями вида: y = f (u),

u =ϕ(x) ,

тогда

152

Лекции 14 – 15

′ = y

′u ′. Например,

y = earctg x ;

y = eu , u = arctg x, y

′

= ? Решение:

y ′

= eu , u

′

y ′ = earctg x

2 .

1 + x

+ x

14.2.5. Логарифмическая производная

При вычислении производной некоторого выражения полезно предвари-

тельное логарифмирование этого выражения.

Рассмотрим функцию y = f (x), y′ = ?

ln y = ln f (x), [ln y]x′ =

y′;

y′

- называется логарифмической производной.

Отсюда y′ = y [ln y]′.

Пример:

1) y = xα , α ≠ 0, y′ = ?

ln y =α ln x,

y′

=α

1 .

xα

′

α−1

y′

y α

x , y′ =α

, (x

)

=α x

y = (sin x)

, y

′

ln y = x

antigtu

ln(sin x) ,

y′

= 2x ln(sin x) + x2

cos x .

sin x

′

{

2x ln(sin x) + x

(sin )

ctg x

}

Пример:

В общем случае для степенно-показательных выражений.

y = f (x)ϕ( x) ln y =ϕ( x) ln f ( x) .

y′ = f (x)ϕ( x) ϕ′

(x) ln f (x) +

ϕ( x)

f ′(x)

f (x)

Пример:

Лог рифмическая производная применяется для вычисления производ-

ной произведения большого числа сомножителей.

1). y = sin x cos x x, y′ = ?

ln y = ln sin x +ln cos x +ln x .

y′

cos x

−sin x

y′ = sin x cos x x ctg x − tg x +

sin x

cos x

Скачано

Производная и дифференциал

153

2). y =

5 x3 (x −1)7

, y′

= ?

x + 6

ln y =

3ln x + 7ln (x −1)− ln (x + 6) ;

′

(ln y)

−

;

x −1

x + 6

y′

x3 (x −1)7

−

x −1

+ 6

x + 6

14.2.6. Производная неявной функции

Пусть уравнение F (x, y (x))= 0 задает неявно функцию y = y(x).

Для

вычисления

y′(x)

нужно

продифференцировать

тождество

F (x, y) = 0 по переменной

x , рассматривая функцию F (x, y (x))

как слож-

ную

функцию

аргумента

x ,

затем

полученное

уравнение

(x, y (x), y′(x))= 0 разрешить относительно

y′(x).

Пример:

antigtu

′

a2 + b2 =1, y

= ? ( y >

0) .

Решение:

Первый сп с б. Выразим явно y из уравнения:

y = ± b

− x2

. Так как y > 0 ,

= b

a2 − x2

y′ =

(a2

− x2 )−

2 (−2x)= −

= − b2

a 2

a2 − x2

Второй способ.

Продифференцируем выражение

=1 по пере-

менной x :

2 y

y′ = 0 , откуда y′ = −

Выр жение для производной y′(x) может зависеть как от x , так и от y .

14.2.7. Производная функции, заданной параметрически

Скачано

154

x ′

Лекции 14 – 15

x = x(t)

Пусть функция y = y(x)задана параметрически:

y = y(t)

Если: 1)

x(t), y(t) - дифференцируемы, 2)

x = x(t) имеет обратную функ-

antigtu

′

цию t = t(x), t (x) , 3)

x (t) ≠ 0 , то yx = .

Доказательство:

y = y(t), t = t(x) . Рассматривая

Рассмотрим функции:

как промежуточ-

ный аргумент, можно считать, что

- сложная функция

x . Тогда

′ = y ′ t ′, t ′

y ′

yt′

x ′

Пример:

x = t2 , y = t3 , yx′ = ?

Решение: x ′ = 2t, y

′ = 3t2 , y ′

= 3t2

= 3 t .

15.1. Производные высших порядков

15.1.1. Определение производной n-го порядка

Скачано

называется произ-

Производной второго порядка от функции y = f (x)

′′

= (

′

водная от ее перв й пр изв дной. Обозначение: f (x)

f (x)) .

Производ ой n -го порядка (или n–й производной) называется произ-

водная первого порядка от производной (n −1)-го порядка.:

f (n) (x) = (f (n−1) (x))′.Т кже используют обозначение y(n) (x) = d n yn .

Пример:

y = sin x, y′ = cos x, y′′ = −sin x, y′′′ = −cos x .

2) y = xn , y′ = nxn−1, y′′ = n(n −1)xn−2 ,…, y(n) = n!, y(n+1) = 0 .

15.1.2. Правила вычисления производной n-го порядка

[ f (x) + g(x)](n) = f (n) (x) + g(n) (x) .

2. Формула Лейбница (производная произведения):

Производная и дифференциал

155

[ f (x) g(x)](n) = ∑Cnk f (n−k ) (x) g(k ) (x) ,

где

Cnk =

число сочетаний

k!(n − k)!

k =0

из n по k , k! (читается k

- факториал) определен для целых неотрицатель-

k =

→ Cn1

= n;

1! =

antigtu

ных k , причем

+1)!

(k +

1) k!, 0!

Пример:

Найти n–ю производную от функции y = eax x2 .

Решение:

f (x) = eax ; g(x) = x2

y = f (x) g(x); где

f (x) = eax ;

g(x) = x2 ;

′

;

′

(x) = a e

(x) = 2 x;

′′

;

′′

(x) = a

(x) = 2;

′′′

(x) = 0;

f (n) (x) = an eax ;

) (x) = 0.

Таким образом, в формуле Лейбница всего 3 ненулевых члена.

Вычисляем коэффициенты:

k =

0 → Cn0 =

=1;

1!(n −1)!

k =

→ Cn2

n(n −1)

;

Скачано

− 2)!

2!(n

(n)

n−1сax

n(n −1)

n−2

(x) = a

+ na

2x +

15.1.3. Вторая производ ая от

еявной функции

Рассмотрим

еяв ую

фу кцию

y = y (x),

определяемую

уравнением

F(x, y) = 0 . Для

отыск ния

второй

производной соотношение

F(x, y) = 0

дифференцируем два р за по переменной x , считая

функцией x , и выра-

жаем y′′ как функцию y и x .

Пример:

x2 + y2 =1, y′′ = ?

2x + 2 y y

′

= 0,

′

+ 2 y

′′

= 0

= − 2 y = − y , 2 + 2 y

y′′ = −

1 +

(y′)2

= −

y2 + x2

156

Лекции 14 – 15

15.1.4. Вторая производная от параметрически заданной функции

Рассмотрим

x = x(t)

= y(t)

′

(y′x )′

или

′′

y′

′

′′x

′ − x

′′y ′

′′

′

x =

yxx

= (yx

)

x =

xt′

yxx = x′

′

Таким образом,

yxx′′

y ′′x ′ −

′′y ′

(xt

)

(xt′)3

15.1.5. Механический смысл второй производной

Пусть

S = f (t)

- закон

движения тела, движущегося поступательно.

Скорость тела V (t )

в данный момент времени:

V (t )= f ′(t) . Если движение

неравномерно, то для приращения времени ∆t

приращение скорости состав-

ляет∆V .

Тогда ∆V

- среднее ускорение тела за промежуток времени ∆t . При ∆t → 0

∆t

получим ускорение в данный момент времени t :

= lim

∆V

antigtu

∆t

=V ′(t) .

a(t )= f ′′(t)

∆t→0

Таким образом,

- ускорение прямолинейного движения равно

второй производной от перемещения по времени.

15.2. Диффере циал фу кции

15.2.1. Пр вила вычисления производной n-го порядка

x (a,b)

Если

функция

y = f (x)

дифференцируема

на

(a,b),

то

lim

∆y

= f

′

∆y

при

∆x → 0 стремится к числу f

′

∆x

(x) . Отношение

∆x

(x) , следо-

∆x→0

∆y

вательно,

отличается

от f

′

на

бесконечно

малую α (x):

∆x

(x)

∆y

′

∆x +α(x) ∆x .

∆x

= f (x)

+α(x), причем lim α (x)= 0 , или ∆y = f (x)

Рассмотрим

′

∆x→0

′

. В общем случае

бесконечно

f (x)∆x

(x) ≠ 0 ,

(x)∆x

Скачано

малая величина первого порядка относительно ∆x при ∆x → 0 .

Производная и дифференциал

157

Поскольку lim

α (x) ∆x

= lim α (x)= 0 , тоα (x) ∆x - бесконечно малая вели-

∆x→0

∆x

∆x→0

чина более высокого порядка, чем ∆x .

antigtu

Главная, линейная по ∆x часть приращения функции называется диф-

′

∆x

ференциалом функции в точке x и обозначается dy = f (x)

Главная часть, потому что α(x) ∆x - бесконечно малая более высокого

порядка малости, чем ∆x . Линейная, потому что дифференциал зависит

от ∆x в первой степени.

15.2.2. Дифференциал независимой переменной

Пусть y = x . Тогда ∆y = ∆x,

y′ = (x)′ =1, dy = dx = ∆x .

Вывод:

дифференциал

независимой

переменной равен ее приращению,

′

dx = ∆x . В общем случае: dy = f (x)∆x

= f (x)dx .

dy =

′

f (x)dx .

Производная может быть записана как отношение дифференциала функ-

ции к дифференциалу независимого переменного (так называемые обо-

′

значения

Лейбница): f (x) = dx

15.2.3. Свойства дифференциалов

Скачано

Поскольку дифференциалы функций вычисляются по основной формуле

dy = y′(x) dx , то справедливы обычные правила дифференцирования.

1. d (c)= 0 ;

2. d (u ± v)= du ± dv;d (u ± c)= du ;

d (uv)= udv + vdu;d (uc)= cdu ;

vdu −udv

15.2.4. Геометри еский смысл дифференциала

Рассмотрим функцию y = f (x) .

Обозна-

чения, приведенные на рисунке, соответству-

ют:

′

, MT - ка-

M (x, y), M (x + ∆x, y + ∆y) , ∆y = NM

сательная в точ е M .

Рассмотрим ∆MNT :

MN = ∆x, NT = ∆x tgϕ , NT = ∆x f ′(x) , dy = NT .

158 Лекции 14 – 15

Дифференциал функции y = f (x) в точке x есть приращение ординаты касательной к графику функции в точке x .

15.2.5. Применение дифференциала к приближенным вычислениям

приближенно дифференциалом этой функции: ∆y dy = f ′(x)dx .

Метод основан на замене приращения функции ∆y = f		(x + ∆x)− f (x)
antigtu	.	ru

Это возможно, так как ∆y и dy отличаются на бесконечно малую вели-

чину o(∆x). lim ∆y =1 + lim

α∆x

=1 + lim

=1.

′

∆x→0

(x)∆x

(x)

Основные рабочие формулы:

x = x0 + ∆x ,

f (x) = f (x0 + ∆x) ≈ f (x0 ) + dy ,

f (x0 + ∆x) ≈ f (x0 ) + f ′(x0 )∆x .

Геометрический смысл: истинная функция на отрезке [x0 , x0

+ ∆x] заменя-

ется линейной функцией, график которой – касательная в точке

(x0 , f (x0 )).

Пример:

Вычислить приближенно 4 15,8 .

Решение:

Пусть y =

4 x ,

=16 .

Тогда y(16)= 4 16 = 2 ;с

′

y = (15,8)= y(16)+ ∆y ; заменим ∆y ≈ dy = y

(x)∆x ;

∆x =16 −15,8 = −0,2 ;

′

4 ′

14−1

1 −3 4

x ;

y (x)= x

′

−3

16 = 4 8 = 32 .

y (16)= 4

Тогда y(15,8)= 2 +

(− 0,2)= 2 − 0,0062 =1,9938 .

Скачано

Пример:

Вычислить приближенно значение объема V шара радиусом r =1,02 м.

Решение:

Так как V

(r)=

r 3 ,

то,

полагая r0

=1 ,

∆r = 0,02 , V ′(r )= 4πr2 и ис-

пользуя формулу для ∆V , получаем:

′

V (1,02) =V (1)+ ∆V ≈V (1)+V

(1) 0,02 = 3

π + 4π 0,02 4, 44 м .

Производная и дифференциал				ru	159

15.2.6. Дифференциал сложной функции			.
Рассмотрим сложную функцию	y =
		f [ϕ(x)], Пусть u – промежуточный
аргумент: y = f (u), u =ϕ(x) . yx′ = fu′ ux′		умножим это равенство на			dx :
yx′dx =		antigtu
	fu′ ux′ dx ,
dy = fu′du .
Сравнение с dy = fx′dx показывает,	что дифференциал функции сохраняет

свою форму независимо от того, является ли ее аргумент x независимой переменной или функцией независимой переменной (промежуточным аргументом).

Это свойство называется свойством инвариантности (неизменности) формы первого дифференциала.

15.2.7. Дифференциалы высших порядков

Пусть y = f (x) - дифференцируемая функция, а ее аргумент x - независимая переменная. Тогда ее первый дифференциал dy = f ′(x)∆x = f ′(x)dx

также является функцией x , от которой в свою очередь можно найти дифференциал.

Дифференциалом второго порядка (или вторым дифференциалом)

функции

f (x)

называет я дифференциал ее дифференциала при фикси-

Скачано

рованном dx .

(dx)

f (x) = d (df (x))

′

′′

= d ( f (x)dx) = dx

d ( f (x)) = dx f

(x)dx = f (x)

′′

; d

f (x) =

′′

= f (x)dx

f (x)dx

Аналогично

определяется

дифференциал

порядка

d n f (x) = d (d n−1 f (x)). Мож о показать, что d n f (x) = f (n) (x)dxn . Здесь

dxn = (dx)n .

1. Для нез висимой переменной d 2 x = 0, d 3 x = 0,…

2. В приведенных формулах предполагалось, что x -

независимая пере-

менная. Если x -

промежуточный аргумент, то форма для второго диф-

ференци ла будет другой, отличной от выражения d

′′

= f (x)dx

Пок жем

это

на

примере

второго

дифференциала.

Пусть

y = f (x),

x = g (t ), t - независимая переменная.

Тогда

d 2 f = d (df )

= d

(

f ′(x)

)

= d

(

f ′(x)

)

dx + f ′(x) d (dx)=

.	ru
160		Лекции 14 – 15

= f ′′(x) dx2 + f ′(x) d 2 x = f ′′(x) (g′(t ))2 dt2 + f ′(x) g′′(t ) dt2 .

Таким образом, в случае сложной функции в выражении для второго диффе-

ренциала появляется дополнительное слагаемое; форма второго дифферен-
циала не инвариантна.	antigtu

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

понятия производной и дифференциала, их геометрический и механический смысл;

правила и формулы дифференцирования;таблицу производных;

способы вычисления производных от сложных функций; функций, заданных неявно и параметрически;

	таблицу производных;
производные высших порядков и правила их вычисления;
	применение дифференциала к приближенным вычислениям.

Скачано		с
Скачано

Лекция 16		.	ru
Лекция 16
ОСНОВНЫЕ ТЕОРЕМЫ АНАЛИЗА.
ПРАВИЛО ЛОПИТАЛЯ – БЕРНУЛЛИ
ФОРМУЛА ТЕЙЛОРА	antigtu
ФОРМУЛА ТЕЙЛОРА

В лекции 16 рассмотрены основные теоремы анализа (Ролля, Лагранжа и Коши), широко использующиеся практически во всех разделах анализа. Излагается правило раскрытия неопределенностей Лопиталя – Бернулли, позволяющее вычислять пределы с помощью дифференцирования. Выводится формула Тейлора, которая при достаточно широких предположениях относительно вида функции дает возможность представить ее приближенно в виде многочлена и оценить допускаемую при этом погрешность.

16.1. Основные теоремы анализа.

16.1.1 Теорема Ролля (о нуле производной)

16.1.2. Теорема Лагранжа (теорема о конечных приращениях) 16.1.3. Теорема Коши (обобщенная теорема о конечных разностях) 16.1.4. Правило Лопиталя – Бернулли. Применение правила Лопиталя

			с
	для раскрытия неопределенностей
	16.1.5. Формула Тейлора. Частные случаи формулы Тейлора.
	Разложение по формуле Маклорена некоторых элементарных функций
	Оценка остаточного члена. Приложения формул Тейлора и Маклорена
	Скачано
16.1. Основные те ремы анализа
16.1.1. Теорема Ролля (о уле производной)
Т	Если: 1) функция	f (x)	- непрерывна на отрезке [a,b], 2) на интервале
	(a,b) существует производная			′
	(a,b) существует производная			f (x) , 3) значения функции на концах от-
	резка совпадают,	f (a) = f (b) ,		то существует точка ξ (a,b)	такая, что
	′
	f (ξ) = 0 .
	Доказательство:	f (x)	непрерывна на [a,b], то на отрезке существуют
	Т к к к функция	f (x)	непрерывна на [a,b], то на отрезке существуют
	н ибольшее M и наименьшее m значения функции.
	Возможны два случая: 1) M = m и 2) M > m .				′
	Рассмотрим: 1) M = m , f (x)			- постоянная, следовательно,	′
	Рассмотрим: 1) M = m , f (x)			- постоянная, следовательно,	f (x) = 0

x (a,b);

162

Лекция 16

2) M > m ,

следовательно,

хотя бы одно из этих значений достигается

внутри [a,b], так как f (a) = f (b) .

Пусть f (ξ) = M , ξ (a,b).

antigtu

Так как

f (ξ) - наибольшее значение

функции, то f (ξ +

x)− f (ξ )≤ 0 при лю-

бом знаке

x .

f (ξ + x)− f (ξ )

≤ 0

, x > 0 ,

f (ξ + x)− f (ξ )

≥ 0, x < 0

переходя к пределу

x →0 и рассматривая отдельно правый и левый

пределы, получаемlim

f (ξ +

x)− f (ξ )

= f ′(ξ ) ≤ 0 ,

x > 0 ,

x→+0

lim

f (ξ +

x)− f (ξ )

= f ′(ξ )≥ 0 ,

x < 0 .

x→−0

′

Эти соотношения совместимы, если f

(ξ) = 0 .

Доказательство для случая, когда во внутренней точке отрезка достига-

ется минимум, проводится аналогично.

Геометрический смысл теоремы Ролля

Скачано

Если функция удовлетворяет условию теоремы Ролля, то в некоторой

точке отрезка касательная к графику параллельна оси 0x .

Теорема Ролля п зв ляет узнать об обращении производной в ноль без

ее вычисле ий.

Если f (x)

такова, что производная существует не во всех точках внутри

′

отрезка [a,b], то может е оказаться такой точки ξ , в которой f (ξ) об-

ращается в ноль.

Пример:

y =

(y0прав )′ =1,

(y0лев )′ = −1.

′

y (0) не существует (по определению).

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

163

16.1.2. Теорема Лагранжа (теорема о конечных приращениях)

Если: 1)

(a,b)

су-

f (x) - непрерывна на отрезке [a,b], 2) на интервале

ществует производная

′

(x) , то существует, по крайней мере, одна точ-

CB = f (b)− f (a) -

угловой коэффициентantigtuсе-

ка ξ (a,b) такая, что

f (b)− f (a) =

′

f (ξ) (b −a).

Доказательство:

Обозначим

f (b)− f

(a)

= Q . Построим F (x)= f (x)− f (a)−Q (x −a).

b − a

F (x) обладает следующими свойствами: 1) непрерывна на [a,b],

2) F′(x) на (a,b), 3) F (a)= F (b)= 0 .

Из теоремы Ролля следует, что существует точка ξ (a,b) такая,

что

F′(ξ) = 0 , F′(x)= ( f (x)− f (a)−Q(x − a))′,

F′(x)= f ′(x)−Q = 0, урав-

нение

f ′(x)−Q = 0

имеет

решение x =ξ , т.е.

f ′(ξ ) = Q ,

или

f ′(ξ ) =

f (b)− f (a)

b − a

Геометрический смысл теоремы Лагранжа

b − a

кущей AB .

Скачано

′

(ξ) - угловой коэффициент касательной к

кривой y = f (x) в т чке x =ξ . На кривой AB

найдется, по крайней мере,

дна т чка M , в

которой касатель ая параллель а хорде AB .

1). Доказанная формула

азывается формулой Лагранжа или форму-

лой

конечных

прир щений. Так

как

a <ξ <b,

то ξ − a <b − a ,

ξ −a =θ (b −a),

где

0 <θ <1,

откуда

ξ = a +θ(b − a) ,

f (b)− f (a)= f ′ a +θ (b

− a)

(b − a).

2). То ек ξ может быть несколько.

3). Если f (a)= f (b), то

f ′(ξ )= 0 , получаем утверждение теоремы Рол-

ля.

4). Теорему Л гранжа можно использовать для приближенных вычисле-

ний:

f (b)− f (a)= f

′ a +θ (b − a) (b

− a), где 0 <θ <1. Положим θ = 1 ,

164

arctg1,1 = ?

.′

Лекция 16

тогда

f (b)− f (a)≈ f ′ a + b

(b − a). Погрешность

тем

меньше, чем

ближе b к a .

antigtu

Пример:

b =1,1 ; a =1, 0 ;

b −a = 0,1; arctg1,1 ≈ arc g1+0,1 (arctg x)

x = 1,1+1,0

= 2,1 .

(arctg x)′ =

;

2,1

≈ 0,5 ,

arct 1,1 ≈

+0, 05 .

+ x2

x= 2

2,1

16.1.3. Теорема Коши (обобщенная теорема о конечных разностях)

Если: 1) f (x),ϕ(x)

непрерывны на [a,b], 2) на (a,b)

существуют про-

изводные f ′(x),ϕ′(x),

ϕ′(x)≠ 0

x ( ,b),

то существует, по край-

f (b)− f (a)

f ′(ξ )

ней мере, одна точка ξ

(a,b) такая, что

ϕ(b)−ϕ(a)

(ξ )

′

Доказательство:

ϕ′(x)

ϕ(b)

≠ϕ(a), так как иначе,

по теореме Ролля,

обратилась бы в

Скачано

ноль, по крайней мере, в одной точке ξ (a,b).

Рассмотрим всп м гательную функцию:

F (x)= f (x)− f (a)

−

f (b)− f (a)

ϕ(x)−ϕ

(a) .

ϕ(b)−ϕ(a)

Она удовлетворяет всем условиям теоремы Ролля, следовательно, суще-

ствует точка ξ (a,b) такая, что F′(ξ )= 0 ,

F′(ξ )= f ′(ξ )−

f (b)− f (a)

ϕ′(ξ )= 0 , f ′(ξ )

f (b)− f (a)

ϕ′(ξ ).

ϕ(b)−ϕ(a)

Разделим на ϕ′(ξ ),

ϕ′(ξ )≠ 0 , получим

f (b)− f (a)

f ′(ξ )

ϕ(b)−ϕ(a)

ϕ′(ξ)

Теорема Лагранжа является частным случаем теоремы Коши.

методами дифференциального исчисления.								antigtu
Рассмотрим F (x)=					f (x)	, где	f (x) и ϕ(x) дифференцируемыru		в неко-
Рассмотрим F (x)=						, где	f (x) и ϕ(x) дифференцируемыru		в неко-
					ϕ(x)
торой окрестности точки a , исключая, быть может, саму точку a . Если при
x → a	f	(x)	и ϕ(x) → 0(∞), функция F (x) имеет в точке a неопределен-
	0			∞
ность	0	или		.
	0			∞

Вычислить lim F (x)

поможет следующая теорема (правило Лопиталя).

x→a

Правило Лопиталя. Если: 1) f (x), ϕ(x) - непрерывны на [a,b];

2) на (a,b)

существуют f ′(x), ϕ′(x), причем ϕ′(x)≠ 0 ;

f (a)=ϕ(a)= 0 ;

существует предел

lim

f ′(x)

, то существует и

ϕ′(x)

x→a

предел lim

f (x)

, причем lim

f (x)

= lim

f ′(x)

ϕ (x)

x→a

′

(x)

Доказательство:

[a,b] точку x ≠ a .

Возьмем на отрезке

Скачано

f (x)

− f (a)

f ′(ξ)

На отрезке [a, x] по теореме Коши

ϕ(x)

−ϕ(a)

ϕ′(ξ)

a <ξ < x ,

ξ -

промежуточная т чка

трезка [a, x].

Но

f (a)=ϕ(a)= 0 ,

з ачит,

f (x)

f ′(ξ )

. Если x → a ,то и ξ → a , сле-

f (x)

ϕ(x)

ϕ′(ξ )

довательно, lim

= lim

ϕ′

(ξ )

= lim

ϕ′

(x)

x→a ϕ(x)

ξ→a

x→a

Более коротко это утверждение формулируют так: предел отношения

двух бесконе но малых функций равен пределу отношения их произ-

водных, если последний существует.

1). Если р ссм тривается предел при

x → ∞,

ϕ(x)→ 0 ,

f (x)→ 0 ,

то

утверждениеостостаетсясправесправедливым: :

f (x)

x =

′

−

f ′

f ′(x)

lim

= lim

ϕ(x)

ϕ′(x)

x→∞

z→0

x→∞

z → 0

′

−

ϕ′

166

Лекция 16

2). Если

f ′(a)=ϕ′(a)= 0 и

f ′(x),

ϕ′(x) удовлетворяют условиям тео-

ремы,

то

можно

применять

правило

Лопиталя

f ′(x)

lim

f ′

(x)

= lim

f ′′(x)

. Правило Лопиталя можно применять не-

ϕ′(x)

(x)

′′(x)

x→a ϕ′

x→a

сколько раз.

3). Без доказательства приведем следующее утверждение:

(x)

∞

′(x)

lim

= lim

ϕ(x)

′(x)

x→a

∞

x→a

Предел отношения двух бесконечно больших функций равен пределу

отношения их производных, если последний существует.

Применение правила Лопиталя для раскрытия неопределенностей

Пример:

lim sin

= lim cos 2x 2 = 2 .

x→0

б)

lim

= lim

= ∞ .

x −sin x

−cos x

sin x

→0

x→0

antigtu

Пример:

∞ .

∞

lim

ax ln a

= ∞ .

= lim

x→∞

12 (x +1)−

б)

lim

x +1

= lim

= 0 .

2 x +1

x→∞

Пример:

a) [0 ∞]=

. f (x)→ 0 , ϕ (x)→ ∞ .

∞

x→a

∞

lim f

(x) ϕ (x)= lim

(x)

= lim

ϕ (x)

∞

x→a

Скачано

(x)

f (x)

∞

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

167

Пример:

ln x

∞

lim x

ln x =[0 ∞]

= lim

= = lim −

= 0

x→0

∞

→0

x→0

−2

Пример:

∞

, 1

. Применяется предварительное логарифмирование, от-

куда следует неопределенность [0 ∞].

Пример:

y = xx , x →0 . lim xx = ?

x→0

Логарифмируем: ln y = x ln x .

Вычислим:

ln x

∞

lim ln y = lim x ln x =[

0 ∞]= lim

= lim

= 0 .

x→0

∞

x→0

−

limln y = 0 ,

ln lim y = 0 , lim y =1,

lim xx =1.

x→0

antigtu

16.1.5. Формула Тейлора

Если f (x)

дифференцируема (n +1)

раз в окрестности точки x0 , то для

любого x

из указанной окрестности справедлива формула Тейлора по-

рядка n:

f ′(x0 )

f ′′(x0 )

f (x)

= f (x ) +

(x − x ) +

(x − x )2

f ′′′(x0 )

f (n) (x0 )

(x − x

+... +

(x − x

+ R

(x),

n+1

где

(x) =

f (n+1) (x +θ(x − x ))

(x − x )

n+1

;

<θ <1.

n+1

(n +1)!

Rn+1(x) называется остаточным членом в форме Лагранжа.

Доказательство:

Обозна им

ϕ(x, x0 )= f (x0 )+

f ′(x0 )

− x0 )+

... +

f (n) (x0 )

(x − x0 )

Скачано

ϕ(x, x0 ) - многочлен n-го порядка (так называемый многочлен Тейло-

ра), Rn+1 (x)= f (x)−ϕ(x, x0 ).

168		Лекция 16
Покажем, что данная формула справедлива. Зафиксируем x		из указан-
ной окрестности, пусть x > x0 . На отрезке [x0 , x]	рассмотрим вспомога-

тельную функцию:

Ф(t) = f (x)−ϕ (x, t)−

(x −t)n+1

Rn+1 (x), где t [x0 , x

(x − x0 )n+1

Поскольку Ф(x0 ) = Ф(x), Ф(t)удовлетворяет условиям теоремы Ролля

и существует точка ξ (x0 , x), в которой Ф′(ξ ) = 0 .

Для вычисления Ф′(t) запишем ϕ(x,t ):

ϕ(x,t) = f (t) +

f ′(t)

(x −t) +

f ′′(t)

(x −t)2 +…+

f (n) (t)

(x −t)n .

Ф′(t) = −ϕt′(x, t)

+ (n +1)

(x − )n

Rn+1 (x).

(x − x )

ϕt′(x, t) = f ′(t) +

f ′′(t) (x −t) −

f ′(t) +

f ′′′(t)

(x −t)2

−

f ′′(t)

2 (x −t) +... +

f (n+1) (t)

−t)n −

f (n)

(t)

n (x − t)n−1

antigtun!

(n+1) (t)

− t)

Следовательно,

−Ф′(t) =

f (n+1) (t)

(x −t)

−(n +

(x −t)n

Rn+1 (x),

(x − x0 )n+1

при t =ξ

Rn+1 (x)=

(n+1) (ξ )

(x − x0 )

n+1

(n +1)!

1).

Формула Тейлора

порядка

позволяет

представить

функцию

y = f (x) в виде суммы многочлена n–й степени и остаточного члена.

2).

Полученная формула для

Rn+1 (x)

дает остаточный член в форме Ла-

Скачано

гранжа, но есть и другие формы остаточного члена, например, в форме Пеано: Rn+1 (x)= o((x − x0 )n ) - бесконечно малая более высокого порядка

малости по сравнению с (x − x0 )n .

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

169

Частные случаи формулы Тейлора

1). При x0 = 0 формула Тейлора называется формулой Маклорена:

f (x) = f (0)+

f ′(0)

x +

′′(0)

x2 +... +

f (n) (0)

xn + R

(x),

antigtu

(

)

(n+1)

(θ x)

xn+1 ; 0 <θ <1.

n+1

+1)!

2). Рассмотрим

f (x)= c0 + c1x1 + c2 x2 +... + cn xn - многочлен порядка n .

Поскольку x

f (n+1) (x)= 0 , то x

Rn+1 (x)= 0 и

f (x)= f (x0 )

f ′(x0 )

− x0 )+... +

f (n)

(x − x0 )

Вывод: по формуле Тейлора любой многочлен порядка n можно представить в виде многочлена по степеням (x − x0 ).

Пример:

Многочлен 2x3 −3x2 + 5x +1 разложить по степеням (x +1) .

Решение:

f (x) = 2x3 −3x2 +5x +1; x0 = −1 ; f (−1) = −9 .

Ищем коэффициенты формулы Тейлора:

′

= 6x

− 6x

+ 5 → f

′

=17;

(x)

(−1)

Скачано

′′

=12x

− 6

→ f

′′

= −18;

(x)

(−1)

′′′

→ f

′′′

=12;

(x) =12

с(−1)

f IV (x) = 0

f (n) (x) = 0;

f (x) = −9 +

17 (x +1) −

18 (x +1)2 + 12 (x +1)3 .

Учитыв я, что 1!= 1; 2!= 1 2 ;

3!=1 2 3 , получим ответ:

2x3 −3x2 +5x +1 = −9 +17(x +1) −9(x +1)2 + 2(x +1)3 .

170	ru	Лекция 16

Разложение по формуле Маклорена некоторых элементарных функций

f (x) = ex ,

f (0)=1,

antigtu

f ′(x) = ex ,

f ′(0) =1,

f ′′(x) = ex ,

f ′′(0) =1,

(n)

(x) = e

(n)

(0) =1.

ex =1+

+... +

+ R

(x),

(x)=

eθx

xn+1 .

1! 2!

n+1

(n +1)!

f (x)= sin x ;

(0)= 0 ,

f ′(x)= cos x = sin

(x + π2 )

;

f ′(0)=1,

f ′′(x)= −sin x = sin (x + 2π2 );

f ′′(0)= 0,

f ′′′(x)= −cos x = sin (x +3π2 );

f ′′′(0)= −1,

……………………………………………..,

f (n) (x)= sin (x + nπ2 ),

(n)

(0)= sin

n π

n – нечетное,

n−1

Скачано

n - четное

(

2 )

(−1) 2 ,

sin x = x − x

+ x

+... +(−1)с

2n+1

+ R

(x).

(2n +1)!

2n+2

Нечетная фу кция sin x разложена по нечетным степеням x .

f (x)= cos x ,

f (0)=1,

f (n) (x)= cos(x + n π2 ),

(n)

(

n – четное,

(0)= cos

n π

n - нечетное

2 )

(−1)2 ,

cos x =1 −

−... + (−1)n

x2n

+ R

(x)

(2n)!

2n+1

Четная функция cos x разложена по четным степеням x .

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

171

(

)

= ln 1 + x

)

(

)

= 0 ,

(

f ′(x)=

f ′(0)=1,

1 + x

f ′′(x)= −

f ′′(0)= −1,

(1+ x)

f ′′′(x)

f ′′′(

0)=1 2 ,

(1+ x)

f (n) (x)=

(−1)n−1 (n −1)!

(n)

(0)=

(−1)

n−1

(n −1)!.

(1+ x)n

ln (1+ x)= x −

−... + (−1)n−1

+ R

(x).

n+1

f (x)= (1 + x)α , где α -любое вещественное число.

(1 + x)α =1+α x +

α(α −1)

x2 +... +

α(α −1)...(α − n +1)

xn + R

(x).

n+1

Частный случай α = n :

antigtu

(

n −1

(1+ x)

=1+ nx +

)

x2 +... + n!x

- формула бинома Ньютона.

Формулы Маклорена для элементарных функций:

xn+1

θ x

1. e

+ x +

+... +

; 0

<θ <1.

(n +1)!

x2n+1

x2n+2

2n + 2

2. sin x = x −

−... +

(−1)

sin(θx +

π);

0 <θ <1.

(2n +1)!

(2n + 2)!

3. cos x =1−

x2n

x2n+1

cos(θx +

2n +1

π); 0 <θ <1.

−... +

(−1)

(

2n)!

(2n +1)!

4. ln(1 + x) = x −

−

+... + (−1)n−1

(−1)n xn+1

;

0 <θ <1.

(n +1)! (1 +θ x)

Скачано

172

n+1

Лекция 16

Оценка остаточного члена

Пусть f (x)

такова, что n и x из окрестности точки x0

f (n) (x)

≤ M .

f (n+1)

(ξ)

antigtu

Рассмотрим остаток: R (x)=

(x − x )n+1 .

x − x.

(n +1)!

n+1

(x)

f (n+1) (ξ)

x − x

n+1

≤ M

x − x0

при n → ∞

n+1

(n +1)!

x − x

n+1

→ 0 и остаточный член может быть сделан сколь угодно малым пу-

(n +1

тем увеличения n .

Итак, если

f (x) обладает указанным выше свойством, то формулу Тей-

лора можно использовать для приближенных вычислений с любой наперед заданной точностью.

Приложения формул Тейлора и Маклорена

1). Для вычисления приближенных значений функций:

f ′(x

)

f (n) (x )

f (x)≈ f (x

)+... +

(x − x

) .

− x

Погрешность (ошибка) вычи ления находится по оценке остаточного

члена.

Rn+1

(x)

≤ε , где ε - погрешно ть.

Скачано

Пример:

Вычислить e с т чн стью ε =10−3 .

Рассм трим

ex , x =1, x

= 0 .

Rn+1 (1)=

eθ

e =1+

+...+

+ Rn+1 (1) ,

0 <θ <1 .

(n +1)!

Rn+1 (1)

, e

< 3

Rn+1 (1)

≤ε .

(n +1)!

n ,

≤ 0,001:

Найдем

наименьшее

удовлетворяющее условию

(n +1)!

n = 6 .

e =1+

+... +

= 1957

= 2,714 .

720

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

2). Для вычисления пределов функций:

Пример:

sin x − x

{x −

3! + 5!

antigtu

+...}− x

− 3! +...

lim

= lim

= −

x→0

В результате изучения материала, изложенного в этих лекциях,

студент должен знать:

теорему Ролля (о нуле производной) и теорему Лагранжа

(о конечных приращениях);

правило Лопиталя – Бернулли раскрытия неопределенностей

и способы его применения к неопределенностям вида

∞

0 ∞

;

, [0

∞], 0

, ∞

, 1

∞

вид многочленов Тейлора для основных элементарных функций.

Скачано

173

		antigtu
	Часть 2
Скачано	с
Скачано

Лекции 1 - 2	.
ИССЛЕДОВАНИЕ ФУНКЦИЙ	.
ИССЛЕДОВАНИЕ ФУНКЦИЙ
И ПОСТРОЕНИЕ ГРАФИКОВ

antigtu
Графическое описание поведения функции очень полезно, так как наглядностьru		гра-

фика делает его незаменимым вспомогательным средством исследования свойств функции. Графики функций, получающиеся из графиков основных элементарных функций с помощью геометрических преобразований, очевидны. Графики сложных функций не могут быть построены без использования дифференциального исчисления. В данных лекциях приводится общая схема исследования функций и ее теоретическое обоснование. Последовательное применение этой схемы позволяет построить график любой сколь угодно сложной функции, возникающей в технических приложениях.

1.1. Исследование функций без привлечения производных 1.1.1. Точки разрыва 1.1.2. Асимптоты графика функции

1.1.3. Вертикальные асимптоты 1.1.4. Горизонтальные асимптоты 1.1.5. Наклонные асимптотыс

1.2. Исследование функций с помощью первой производной 1.2.1. Монотонность функции 1.2.2. Локальный эк тремум функции

1.2.3. Необходимые условия эк тремума Скачано1.2.4. Достаточные условия экстремума

1.2.5. Правило отыскания экстремумов функции 2.1. Исследование функций с п мощью второй производной

2.1.1. Исслед вание функций на максимум и минимум с помощью вт р й произв дн й 2.1.2. Направле ие выпуклости и точки перегиба кривой

2.2. Общая схема исследова ия функции и построения графика 2.3. Примеры исследова ия функций

1.1. Исследование функций без привлечения производных

Построение гр фика функции y = f (x) применяется, как правило, для

возможно более точной характеристики хода изменения функции, точность расположения отдельных точек графика обычно представляет меньший интерес.

x→x0 +0

x→x0

176

Лекции 1 - 2

1.1.1. Точки разрыва

Функция y = f (x) называется непрерывной в точке

x0 , если функция

определена

точке

существуют

пределы

lim

f (x) =

antigtu

x→0

x→x0 −0

= lim

f (x) = lim f (x), и при этом lim f (x) = f (x0 )

Точка x0 , в которой функция y = f (x) обладает свойством.

непрерывно-

сти, называется точкой непрерывности функции, в противоположном

случае точка x0

называется точкой разрыва функции.

Если

односторонние

пределы

существуют,

причем

lim

f (x) =

x→x0 −0

= lim

f (x) и функция y = f (x) не определена в точке x0 или нарушено

x→x0 +0

то точка x0

условие lim f (x) = f (x0 ) ,

называется точкой устранимого

x→x0

разрыва.

Пример:

Исследовать поведение функции

f (x)= sinx

в точке x0 = 0 .

В точке x0 = 0

функция не определена, т.е. x0

= 0 - точка разрыва.

В теории пределов был доказан 1-й замечательный предел lim sinx =1,

следовательно,

lim sinx

= lim sinx =1 и

x0 = 0

является точкой устрани-

Скачано

x→+0

x→−0

мого разрыва.

= 0 , доопределим ее, по-

Чтобы функция стала непрерывной в точке

ложив

f (0)= lim f

(x)=1 (так называемое доопределение по непрерыв-

x→0

sinx

, x ≠ 0,

ности).

Новая,

будет не-

доопределенная функция f (x)= x

x = 0

прерывна на новой области определения – всей числовой оси.

Если

односторонние

пределы

существуют,

причем

lim f (x) ≠

lim f (x),

то точка х0 называется точкой разрыва 1-го ро-

x→x0 −0

x→x0

да.

Пример:

Исследовать поведение функции y =

в точке x0 = 0 .

В точке x0 = 0

функция не определена, так как знаменатель равен нулю,

т.е. x0 = 0 - точка разрыва.

Исследование функций и построение графиков

177

По определению модуля

если

x ≥ 0;

−x,

если

x < 0.

Левый предел: lim =

= lim

−x

= lim (−1)= −1 .

x→−0

Правый предел: lim =

= lim

= lim 1 =1 .

x→+0

Односторонние пределы конечны, но не равны друг другу., следователь-

но, точка x0 = 0 является точкой разрыва 1-го рода.

Если хотя бы один из односторонних пределов не существует или бес-

конечен, то точка x0 называется точкой разрыва 2-го рода.

Пример:

Определить точки разрыва функции f (x)= e x

и исследовать характер

разрыва.

Решение:

= 0 . Вычислим левый предел, учитывая,

Функция разрывна в точке

что lim ex = 0 . Так как lim

= −∞

, lim ex = 0 .

x→−∞

x→−0

Вычислим правый предел, учитывая, что lim ex = ∞. Так как lim 1 = +∞,

x→+∞

x→+0

antigtu

lim ex = ∞ . Правый предел бе конечен, точка

x0 = 0

является точкой

x→−0

разрыва 2-го рода.

1.1.2. Асимптоты графика фу кции

Если расстояние от точки,

лежащей на кривой,

до некоторой прямой

стремится к нулю при неограниченном удалении этой точки от начала

координат, то эта прям я называется асимптотой кривой. Асимптоты

могут быть вертикальными, горизонтальными и наклонными.

1.1.3. Вертикальные асимптоты

Прям я x = x0 является вертикальной асимптотой графика функции

y = f (x),

если хотя бы одно из предельных значений

lim f

(x) или

lim f (x)

x→x0 −0

равно +∞ или−∞.

x→x0 +0

Скачано

178							Лекции 1 - 2
	Так, график функции y = 1 имеет вер-				.	ru
				x
тикальную асимптоту x = 0 , поскольку
lim	1 = −∞ ,	lim	1 = +∞.	antigtu
x→0−0	x	x→0+0	x
	Для разыскания вертикальных асим-
птот кривой y = f (x)
1)	находим	на	оси Ox	точки разрыва
функции f (x);
2) выделяем те из них, в которых хотя бы
один из пределов функции				f (x) (слева или

справа) равен +∞ или −∞. Пусть это будут точки x1, x2 ,..., xm , тогда прямые

x = x1

x = x2 ,…, x = xm будут вертикальными асимптотами графика функции

y = f

(x).

Например,

для кривой

y =

вер-

x2 −1

тикальными асимптотами

будут

прямые

x = −1

x =1.

Вертикальная

прямая

x = x0

может оказаться

асимптотой гра-

фика функции

y = f (x)

и в том

лучае,

когда точка x0

является концом интерва-

Скачано

f (x).

ла, в котором определена функция

Это будет тогда, когда

- левый конец

интервала

lim

f (x)= +∞

или

-∞, либо когда x0 - правый конец интерва-

x→x0 +0

ла lim f

(x)= +∞

или

-∞. Например, функция y = ln x определена в ин-

x→x0

−0

тервале 0 < x < +∞,

и для

ее

lim ln x = −∞, так что прямая x = 0 (ось Oy )

x→0+0

является вертик льной симптотой графика функции y = ln x .

1.1.4. Горизонтальные асимптоты

Прямая y = b называется правой горизонтальной асимптотой графика

функции y = f (x)	, если	lim	f (x)= b .
Прям я y = b		x→+∞
Прям я y = b	называется левой горизонтальной асимптотой графика
фун ции y = f (x)	, если	lim	f (x)= b .
		x→−∞

Функция f (x) в этом случае представима в виде f (x)= b +α(x), где

lim α (x)= 0 .

x→±∞

Исследование функций и построение графиков

179

Возможны следующие ситуации:

1) не существует ни левой, ни правой горизонтальной

асимптоты ( f (x) = x2 );

2) существует левая горизонтальная асимптота и не

существует правой ( f (x)= ex , lim f (x)= 0 , y = 0 - ле-

x→−∞

вая горизонтальная асимптота);

3) существует правая горизонтальная асимптота и не

существует левой ( f (x) = e−x ,

lim f

(x) = 0 , y = 0

x→+∞

правая горизонтальная асимптота);

4) обе горизонтальные асимптоты существуют, но не

совпадают ( f (x) = arctgx , lim f

(x)= −π ,

y = −π

- ле-

x→−∞

antigtu

вая горизонтальная асимптота;

lim f

(x)=π , y

=π

x→+∞

правая горизонтальная асимптота;

5) обе горизонтальные асимпт ты существуют и сов-

падают ( f (x)=

, lim f (x)= lim f

(x)= 0 , y = 0 -

урав-

x→−∞

x→+∞

нение обеих горизо таль ых асимптот).

Скачано

1.1.5. Наклонные асимптоты

Прямая y = kx + b называется правой наклонной асимптотой графика

функции y = f

(

)

, если lim

(

)

− kx −b

)

= 0 .

x→+∞ (

В этом случ е функция

(x) представима в виде f (x)= kx + b +α (x),

где lim α (x)= 0.

x→+∞

Существование асимптоты y = kx + b у кривой y = f (x) при x → +∞ означает, что при x → +∞ функция y = f (x) ведет себя «почти как линейная

180	ru	Лекции 1 - 2

функция», т.е. отличается от линейной функции y = kx + b на бесконечно ма-

лую функцию при x → +∞.	.

Т Для того чтобы график функции y = f (x) имел при x → +∞ наклонную асимптоту y = kx + b , необходимо и достаточно, чтобы существовали два

предела:

(x)

1) lim

= k ;

lim

(x)− kx = b .

x→+∞

Доказательство:

Необходимость.

Пусть

график

функции

y = f (x)

при

x → +∞

имеет

асимптоту

y = kx + b ,

т.е.

для

(x)

справедливо

f (x)= kx + b +α (x), α(x)

→ 0 при x → +∞ .

f (x)

(x)

Тогда lim

= lim

k +

= k ,

x→+∞

lim f (x)

− kx = lim b +α (x) = b.

x→+∞

Достаточность.

Пусть существуют оба предела k

и b . Существование

предела для b позволяет утверждать, что разность

f (x)− kx −b является

бесконечно малой функцией при x →antigtu+∞ . Обозначив эту разность через

α (x), получим

f (x)= kx + b +α (x), где α(x)→ 0 при x → +∞ . Это оз-

начает, что график

функции

y = f (x) имеет наклонную асимптоту

y = kx + b . Анал гично исследуетсяс

случай x → −∞.

Пример:

Найти

асимптоты

графика

функции

y =x+arctgx .

lim

x +arctg x

= k+ = lim

x +arctg x

= k− =1,

x→+∞

x→−∞

b+ = lim

(arctg x)= π

x→+∞

b− = lim

(arctg x)= −

π ,

график

имеет две

x→−∞

несовпадающие наклонные асимптоты: ле-

вую y = x − π

и правую

y = x +

π .

Скачано

Исследование функций и построение графиков

181

Пример:

Построить

график

функции

+ 2x −3

+ x − 2

без использования производной.

antigtu

Решение:

Преобразуем выражение:

x2 + 2x −3

x +3

x2 + 2x −3

−1)(x + 3)

, ,

x2 + x −

−1)(x + 2)

x2 + x −2

x + 2

( x ≠1),

x + 3

= 1 +( x + 2 )

+1,

x + 2

x +

x + 2

т.е. y =

+1 , ( x ≠1). График этой функ-

x + 2

1 на две единицы влево, на од-

ции получается смещением графика y =

ну единицу вверх и выкалыванием точки графика с абсциссой x =1.

1.2. Исследование функций с помощью первой производной.

1.2.1. Монотонность функции

Пусть функция

f (x)

определена на отрезке

[a,b]. Если для любых

, x2 [a,b] из условия x1 < x2

ледует неравенство:

Скачано

f (x)

f (x1 )≤ f (x2 )

, то функция

неубывающая на

[a,b];

f (x1 )< f (x2 ),

то функция

f (x)

возрастающая

[a,b];

f (x1 )≥ f (x2 ),

то фу кция

f (x)

невозраст ющ я на [a,b];

f (x1 )> f (x2 ),

то функция

f (x)

убывающая на [a,b].

Функции всех этих типов носят общее название монотонных; возрас-

тающие и убывающие функции называются строго монотонными.

Пусть функция

f (x): 1) непрерывна на отрезке [a,b]; 2) имеет произ-

водную f '(x) по крайней мере на интервале (a,b).

Для того чтобы функция

f (x)

на отрезке [a,b]

была неубывающей (не-

возрастающей), необходимо и достаточно выполнение условия f '(x)≥ 0

182

Лекции 1 - 2

( f '(x) ≤ 0 ) для всех точек x из интервала (a,b).

Доказательство:

Необходимость. Пусть функция f (x) является неубывающей

на отрезке

[a,b]. Докажем,

что на интервале

(a,b)

производная

f '(x) ≥ 0 . Возьмем точки x и x + ∆x в интервале (a,b)

Так как по усло-

вию f (x)

неубывающая, то при любом ∆x

(положительном или от-

рицательном) знак ∆x

и f (x + ∆x)− f (x) один и тот же, и поэтому

f (x + ∆x)− f (x)

≥ 0 .

∆x

Учитывая, что по условию в каждой точке x интервала (a,b)

существу-

ет производная f '(x), из последнего равенства получим

f '(x)

= lim

f (x +∆x)− f (x)

≥ 0 .

∆x

∆x→0

Итак, в любой точке интервала (a,b) имеем f '(x)≥ 0 .

Достаточность. Пусть

f '(x)≥ 0

на интервале (a,b). Докажем, что функ-

ция f (x) - неубывающая на отрезке [

,b]. Действительно, пусть x1 < x2

- любые две точки отрезка [a,b].

По теореме Лагранжа

− f

x antigtu= f ' ξ x − x

, где x <ξ < x . Так

( 2 )

( 1 )

( )( 2

1 )

как f '(x)≥ 0 в каждой точке x интервала (a,b), то и

f '(ξ )≥ 0 . Кроме

того x2 > x1 . Поэтому

f (x2 )≥ f (x1 ). Итак, из неравенства x1 < x2 следует

неравенство f (x1 )≤ f (x2 ),

функ-

а это и означает, что на отрезке [a,b]

ция f (x) неубывающая.

f '(x)

Таким образом, и тервалы знакопостоянства производной

явля-

ются интервалами мо ото

ости функции

f (x).

Справедливо следующее утверждение (достаточное условие возрастания

функции): если

f '(x)> 0 на интервале (a,b), то f (x) на отрезке

[a,b] воз-

растает. Одн ко если f (x)

возрастает на

[a,b], то отсюда не следует, что

f '(x)> 0 всюду на интервале (a,b).

Скачано

Пример:

Функция f (x) = x3 возрастает на отрезке [−1,1], однако ее производная f '(x)= 3x2 обращается в нуль в точке x = 0 .

Рассмотрим возрастание или убывание функции в точке.

Исследование функций и построение графиков

183

Функция

f (x)

называется возрастающей в точке x = x0 ,

если сущест-

вует

такая окрестность

(x0 −δ, x0 +δ )

точки

x0 , в которой для

всех

x < x0

имеем f (x) < f (x0 ), а для всех x > x0 верно f (x) > f (x0 )

Функция f (x)

antigtu

называется убывающей в точке x = x0 , если существует

такая окрестность (x

−δ, x

+δ ) точки

x , в которой для всех

x < x

имеем f (x) > f (x0 ), а для всех x > x0

верно f (x) < f (x0 ). .

Следующая теорема выражает достаточные условия возрастания и

убывания функции в точке.

Пусть функция

f (x)

в точке

x = x0

имеет производную

f '(x).

Если

f '(x0 ) > 0 , то функция

f (x)

в точке

возрастает; если

f '(x0 ) < 0 , то

f (x)

в точке x0 убывает.

Доказательство:

Пусть f '(x0 ) > 0 . Это означает, что

lim

f (x0

+ ∆x)− f (x0 )

0 .

∆x→0

∆x

Но тогда существует такое

δ > 0 , что

для всех

∆x , удовлетворяющих у ло-

вию 0 <

∆x

<δ , верно неравен тво

Скачано

f (x0 + ∆x)− f (x0 )

> 0 .

∆x

<δ величины f (x0 + ∆x)− f (x0 )

и ∆x

Отсюда следует, что при 0 <

имеют один и т т же знак: если ∆x <0,

то и

f (x0 + ∆x)− f (x0 )<0,

т.е.

f (x0 + ∆x)< f (x0 ); если

же

∆x >0,

то и

f (x0 + ∆x)− f (x0 )>0,

т.е.

f (x0 + ∆x)> f (x0 ). Согласно определению, это и означает, что функция

f (x)

в точке x0 возр стает.

f '(x0 )< 0 , то функция f (x) в

Аналогично можно док зать, что если

точке x0 убыв ет.

184								Лекции 1 - 2
		Теорема дает достаточные,			но не необходимые условия возрастания и
	!	Теорема дает достаточные,			но не необходимые условия возрастания и
		убывания функции в точке. Так, функция, гра-				.	ru
		убывания функции в точке. Так, функция, гра-
		фик которой приведен на рисунке, возрастает в
		точке x = 0 , но в этой точке производная функ-
		ции не существует.
		Функция		f (x)= x3 возрастает в точке x = 0 , но
		ее производная f '(x) в точке x = 0 обращается
		ее производная f '(x) в точке x = 0 обращается
		в нуль.
	1.2.2. Локальный экстремум функции
		Пусть функция f (x) определена в некото-
	О	Пусть функция f (x) определена в некото-
		рой окрестности точки x0 ,			включая и саму
		рой окрестности точки x0 ,			включая и саму
		точку x0 . Точка x0 называется точкой ло-
		кального максимума (минимума) функ-
		ции	f (x), если существует такое δ > 0 , что
		для	всех	x из интервала	(x0 −δ, x0 +δ )

	верно неравенство:				antigtu

	∆f = f (x)− f (x0 ) ≤ 0 ( ∆f = f (x)− f (x0 ) ≥ 0 ).
О	Значение функции		f (x)	в точке максимума называется локальным
	максимумом, а значение функции в точке минимума - локальным ми-
	нимумом данн й функции. с
	Локальные максимум и минимум называются локальными экстрему-
	мами.
	Эти определе ия оз ачают, что				f (x0 ) - ло-
кальный м ксимум функции				f (x),	если суще-
ствует такой интерв л (x0 −δ,				x0 +δ ), в котором
f (x0 ) является н ибольшим значением функ-
ции	f (x), и	f (x0 ) - локальный минимум функ-
ции	f (x),	если	существует		интервал

ле.

(x0Скачано−δ, x0 +δ ), в котором f (x0 ) является наименьшим зн чением функции на этом интерва-

Термин локальный (местный) обусловлен тем, что введенное понятие

экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. В дальнейшем слово «локальный» бу-

Исследование функций и построение графиков

185

дем для краткости опускать. Мы будем рассматривать лишь точки строгого

максимума и минимума.

Точка x0

называется точкой строгого максимума (минимума) функции

f (x), если существует δ > 0 такое, что для всех

x ,

удовлетворяющих

условию 0 <

x − x

<δ , верно строгое неравенство

(

)

− f

x ru

< 0 (со-

( 0 )

ответственно

f (x)− f (x0 )> 0 ). В приведенном определении не предпо-

лагается непрерывности функции f (x) в точке x0 .

Пример:

x ≠ 0,

y = x

x = 0,

В точке 0 - максимум, хотя в ней нет не-

прерывности функции.

1.2.3. Необходимые условия экстремума

Функция

f (x)

antigtu

может иметь эк тремум только в тех точках, в которых

ее производная

f '(x)

либо равна нулю, либо не существует.

Доказательство:

сf (x) имеет

Пусть в точке x0 функция

производную и

f '(x0 )≠ 0 . Пусть для оп-

ределенности

f '(x0 )> 0 . Тогда функция

f (x) в точке x0

будет возрастающей. По-

этому найдется такое δ > 0 ,

что для всех

x из интерв ла

(x0 −δ, x0 )

верно нера-

венство

f (x)< f (x0 ),

для всех x из ин-

тервала

(x0 , x0 +δ )

верно

неравенство

f (x)> f (x0 ).

Из этого следует, что не существует окрестности точки x0 , в которой ве-

личина f (x0 )

была бы наибольшим или наименьшим значением функ-

ции f (x), и поэтому точка x0 не будет ни точкой максимума, ни точкой

минимума функции

f (x). Аналогичными рассуждениями придем к то-

му же выводу при f '

(x0 )< 0 .

Скачано

186							ru	Лекции 1 - 2
186								Лекции 1 - 2
			Итак, если в точке x0 существует произ-			.
	водная f '(x0 ) ≠ 0 , то в точке x0 не может быть					.
	ни максимума,			ни минимума функции f (x).
	Следовательно,			экстремум функции	antigtu
	Следовательно,			экстремум функции	f (x) мо-
	жет быть только в такой точке, в которой про-
	изводная f '(x)			либо равна нулю, либо не су-
	ществует, что показано на рисунке.
	Функция y = f (x) имеет экстремумы в точках x1, x2 , x3 , x4 ; при этом в точках
	x1	и x4 производная f '(x) не существует, а в точках x2 и x3 она равна нулю.
	О		Точки, в которых выполняется необходимое условие экстремума для
			функции	f (x), называются критическими точками этой функции.
			Они определяются как корни уравнения f '(x) = 0 и как точки, где f '(x)
			не существует (в частности, где f '(x) - бесконечно большая функция).
			Корни уравнения f '(x)= 0 называют стационарными точками функ-
			ции f (x): скорость изменения		f (x) в такой точке равна нулю.

Утверждение, обратное к теореме, неверно: не в каждой своей критической точке функция f (x) обязательно имеет максимум или минимум.

Например, для функции f (x)= x3

'(0)= 0 , поэтому точка x = 0 явля-

Скачано

f (x)= x3

в точке x = 0

ется критической для данной функции. Но функция

экстремума не имеет: f (0)= 0 ,сдля

x < 0

f (x)< 0 ,

для x > 0

f (x)> 0 , так

что

точке

x = 0

данная

функция

возрастает.

Для

функции

xsin

x ≠ 0,

в точке x = 0

производная не существует, однако

f (x) =

0, x = 0

экстремум отсутствует.

1.2.4. Достато ные условия экстремума

Пусть x = x0

– критическая точка для функции

f (x)

и функция f (x)

непрерывна в точке x0 .

что для всех x из интервала (x0 −δ, x0 )

Пусть существует такое δ > 0 ,

производная

f '(x)> 0, а для всех x

из интервала (x0 , x0 +δ )

f '(x)< 0 ,

то есть при переходе x через точку x0 производная f '(x)

меняет знак с

плюса на минус. Тогда в точке x0 функция

f (x)

имеет максимум.

Исследование функций и построение графиков

187

Доказательство:

f '(x) > 0

Так

как по условию

интервале

(x0 −δ, x0 ), то на отрезке

[x0 −δ, x0 ]

функция

f (x) возрастает;

так как f '(x) < 0

antigtu

в интервале

(x0 , x0 +δ ), то на отрезке

[x0 , x0 +δ ]

функция

f (x) убывает. Следовательно, f (x0 )

есть наи-

большее значение функции

f (x)

в окрестности (x0 −δ, x0 +δ )

точки

x0 , а

это означает, что f (x0 ) есть локальный максимум функции

f (x).

Пусть x = x0

– критическая точка для функции

f (x)

и функция

f (x)

непрерывна в точке x0 .

из интервала (x0 −δ, x0 )

Пусть существует такое δ > 0 , что для всех x

производная

f '(x)< 0 , а для всех x из интервала (x0 , x0 +δ ) имеем

f '(x)> 0, то есть при переходе x через точку x0 производная

f '(x) ме-

няет знак с минуса на плюс. Тогда в точке x0 функция f (x) имеет ми-

нимум.

1.2.5. Правило отыскания эк тремумов функции

Скачано

Чтобы найти точки максимума и минимума функции f (x), надо:

1).

Найти производную

f '(x), приравнять ее к нулю и решить полученное

уравнение f '(x)= 0.

2).

Найти точки, в которых производная f '(x) не существует. Эти точки и

корни уравнения f '(x)= 0 будут критическими точками для функции

f (x).

3).

Исследовать знак производной f '(x) слева и справа от каждой критиче-

ской то ки. Если при переходе x через критическую точку x0 произ-

водн я f '(x) меняет знак с плюса на минус,

то в точке

функция

f (x) имеет м ксимум; если знак

f '(x) меняется с минуса на плюс, то в

точ е x0 функция

f (x) имеет минимум. Если при переходе

через

ритичес ую точку

знак

f '(x) не меняется, в точке

функция

f (x) не имеет ни максимума, ни минимума.

188

Лекции 1 - 2

f ′(x0

− ∆x)

f ′ (x0 )

f ′(x0 + ∆x)

Экстремум

нет

> 0

0, ± ∞,

> 0

max

> 0

0, ± ∞,

< 0

antigtu

min

< 0

0, ± ∞,

> 0

< 0

0, ± ∞,

< 0

нет

2.1. Исследование функций с помощью второй производной

2.1.1. Исследование функций на максимум и минимум

с помощью второй производной

Т Пусть в точке x0 функция f (x)

имеет первую и вторую производные,

причем f '(x0 )= 0 , а

f ''(x0 )≠ 0 . Тогда в точке x0 данная функция f (x)

имеет максимум, если f ''(x0 )< 0 , и минимум, если f ''(x0 )> 0 .

Доказательство:

f (x), так

Точка x0 является критической точкой для данной функции

как f '(x0 )= 0 . Пусть

f ''(x0 )< 0 . Из этого следует, что в точке x0 первая

производная

f '(x)

убывает, то

е ть

существует такая окрестность

(x0 −δ, x0 +δ ) точки x0 , что для в ех

x из интервала (x0 −δ, x0 ) верно

Скачано

(x0 , x0 +δ )

неравенство

f '(x)>

f '(x0 )= 0 , а для всех x

из интервала

верно f '(x)< f '(x0 )= 0 .

Таким образом, при перех де x через критическую точку x0 производная f '(x) меняет свой з ак с плюса на минус. Следовательно, функция f (x) в точке x0 имеет максимум.

Подобными же р ссуждениями доказывается, что если в критической
точке x0 втор я производная		f ''(x0 )> 0 , то функция f		(x) в точке x0
имеет минимум.

	f ′(x0 )	f ′′(x0 )	Экстремум
	0	< 0	max
	0	> 0	min
	0	0

Исследование функций и построение графиков

189

2.1.2. Направление выпуклости и точки перегиба кривой

Пусть кривая задана уравнением y = f (x)

и пусть функция f (x)

в точке x0

имеет ко-

antigtu

нечную производную f '(x0 ), то есть в точке

M 0 (x0 ,

f (x0 )) существует касательная к дан-

ной кривой, не параллельная оси Oy .

Если существует

такая

окрестность

(x0 −δ, x0 +δ ) точки x0 ,

что все точки

данной кривой, абсциссы которых содер-

жатся в этой окрестности, расположены

выше касательной к кривой в точке

M0 ,

то говорят, что выпуклость данной кри-

вой в точке M0 направлена вниз.

Если все точки кривой с абсциссами из

некоторой окрестности точки x0 находят-

ся ниже касательной к этой кривой в точ-

ке M 0 , то говорят,

что выпуклость данной кривой в данной точке на-

правлена вверх.

Скачано

y = f (x), дифференцируемой на

Будем говорить, что график функции

интервале (a,b), имеет на этсм интервале выпуклость, направленную

вверх (вниз), если график эт й функции в пределах интервала (a,b) ле-

жит не выше ( не ниже) люб й своей касательной. О графике, выпуклом

вверх, часто говорят как о просто выпуклом, график, выпуклый вниз,

называется вог утым.

Если во всех точк х интервала (a;b)

функция f (x)

имеет отрицатель-

ную вторую производную ( x (a;b)

f ''(x)< 0 ), то график функции в

этом интервале выпуклый вверх. Если x (a;b)

f ''(x)> 0 - график

выпуклый вниз.

Точка М0 (x0 , f (x0 )) называется точкой

перегиба ривой y = f (x), если:

в точ е x0 существует касательная;

существует такая окрестность

(x0 −δ, x0 +δ ) точки x0 , что для x < x0

из

190

Лекции 1 - 2

этой окрестности выпуклость кривой направлена в одну сторону, а при

x > x0 - в противоположную.

Точка М0 (x0 , f (x0 ))

может

быть

точкой перегиба

кривой

y = f (x),

только если

f ''(x0 )= 0

(или

f ''(x0 )

не существует)

Это

условие

не

функции

является достаточным. Так, например, для

f (x)= x

имеем

f ''(x)=12x

и f ''(0)= 0 , но точка O(0,0) не является

точкой перегиба кривой y = x4 : в этой точке выпуклость кривой направ-

лена вниз.

Пусть функция

f (x)

имеет вторую про-

изводную в некоторой окрестности точки

x0 ,

непрерывную в

точке

x0 .

Если

f ''(x0 )= 0

и при переходе

через точку

вторая

производная

f ''(x)

меняет

знак, то точка М0 (x0 , f (x0 ))

есть точка

перегиба кривой y = f (x).

y = f (x) имеет в точке

М0 (x0 , f (x0 )) каса-

Обобщение.

Пусть кривая

antigtu

тельную, параллельную о и Oy . Пу ть функция f (x) в некоторой окрестно-

Скачано				самой точки x0 , имеет непрерывную вто-
сти точки x0	, кроме, быть может,			самой точки x0 , имеет непрерывную вто-
рую производную. Если		f ''(x)	в точке x0 равна нулю или не существует и
при переходе x через т чку x0			пр изводная f ''(x)			меняет свой знак, то точ-
ка М0 (x0 , f (x0 )) - т чка перегиба кривой y = f (x).
f ′′(x0 − ∆x)	f (x)	f ′′(x0 )			f ′′(x0 + ∆x)	f (x)	Перегиб
> 0	вып. вниз	0,			> 0	вып. вниз	нет
> 0	вып. вниз	0,			< 0	вып. вверх	есть
< 0	вып. вверх	0,			> 0	вып. вниз	есть
< 0	вып. вверх	0,			< 0	вып. вверх	нет

Исследование функций и построение графиков											191
2.2. Общая схема исследования функции и построения графика
1.		Найти область определения функции; найти область значений функции;
		найти точки пересечения графика с осями координат, указать интервалы
		знакопостоянства функции.
2.		Проверить функцию на периодичность; проверить функцию на четность
		и нечетность.							.	ru
3.		и нечетность.

		Исследовать функцию на непрерывность, найти точки разрыва функции
		и ее односторонние пределы в этих точках; определить наличие гори-
		зонтальных, вертикальных и наклонных асимптот.
4.		Вычислив первую производную, найти критические точки и интервалы
		монотонности функции, выделить точки локальных экстремумов.
5.		Вычислив вторую производную, найти интервалы выпуклости и точки
		перегиба графика функции.
6.		Построить график.
2.3. Примеры исследования функций
	Пример:
		Найти экстремумы функции f (x)= 3x2 3					− x2 .
		Решение:				antigtu
		Решение:
		f ′(x)= 2	1 −2x ,	2	− 2x = 0 x1 = −1, x2 =1,
			3 x	3 x
		f ′(x) не существует в т счке х3 = 0 .
		х	(−∞; −1)	-1	(−1;0)	0	(0;1)	1	(1;∞)
		f (x)	/ 2		2 0		/ 2		2
		f ′(x)	+	0	–		+	0	–
				max		min		max
		Вид гр фика функции f (x)= 3x2 3 − x2 :							2
		Скачано							1.5
									1
									0.5
							-2	-1		1	2

192

Лекции 1 - 2

Пример:

Построить график функции y = xe−4 x .

Решение:

1). x (-∞,∞), х0

= 0; y0 = 0 - точка пересечения с осями

2). Функция общего вида.

antigtu

3). f(x) – непрерывна всюду вертикальных асимптот нет

= lim

= 0

= lim

= 0 ,

x→∞ e4 x x

x→∞ e4 x

y1 = 0 - наклонная (горизонтальная) асимптота при х →∞;

k2 = lim

= ∞ наклонных асимптот при х →-∞ нет.

x→−∞ e4 x x

= 1 .

4). y′ = e-4x − 4xe−4 x = e−4 x (1 − 4x )

y′ = 0 x

1 .

5). y′′ = -4e-4x

− 4e−4 x

+16xe−4 x

= e−4 x (16x −8) , y′′ = 0 x 2 =

;

−∞;

;∞

2e2

y′

–

y′′

–

∩

max

∩

перегиб

Вид графика функции y = xe−4 x :

Скачано

Пример:

Исследовать фу кцию y =

и построить ее график.

2 (x +1)2

Реше ие:

1). Функция определена всюду, кроме точки x = −1.

Н йдём точки пересечения графика с координатными осями. Для этого

решим уравнения

= 0 и

y = 0 .

х0

= 0; y0

= 0 - точка пересече-

2(x +1)2

ния с осями.

2). Функция общего вида.

3). Точка x = −1 является точкой разрыва 2-го рода. Отсюда следует, что

гр фик функции имеет вертикальную асимптоту x = −1.

Выясним, существуют ли наклонные асимптоты. Вычислим пределы:

k = lim

f (x)

= lim

;

2(x

+1)2

x→∞

Исследование функций и построение графиков

193

b = lim(

−

x) =

lim

− 2x2

− x

= −1.

x→∞ 2(x +

1)2

2 x→∞ (x +1)2

y = 1 x −1 является наклонной асимптотой.

antigtu

ласть вогнутости.

4). Находим производную: y′ =

2(x +1)3

Знак производной определяется знаком дроби

x + 3

x +1

. Легко получить, что

приx < −3 и x > −1

y′ > 0 , а при −3 < x < −1

y′ < 0 . Интервалы возрас-

тания есть (−∞;−1)

и (−1;∞) ; интервал убывания (−3;−1) . В области оп-

ределения функции производная существует всюду и обращается в нуль

приx = −3 и x = 0 .

При x < −3 y′ > 0 ,

а приx > −3

y′ < 0 . Следовательно, точка x = −3 яв-

ляется точкой максимума.

Находим значение функции при

x = −3 : y( −3 ) = ( −3 )3

= −

= −3,375.

При переходе через другую критическую точку x = 0 производная знак

не меняет, т.е. x = 0 не является точкой экстремума.

5). Находим вторую производную y′′ =

. Видим,

что y′′ < 0 при

( x +1)

является областью выпуклости. y′′ < 0 , также

x < −1, интервал ( −∞;−1)

при −1 < x < 0 - это тоже область выпуклости;

′′

> 0 при x > 0 - это об-

В области определения функции y′′существует всюду;

y′′ = 0 при x = 0 .

Скачано

меняет знак,

то

x = 0 есть абс-

Так как при переходе через эту точку y′′

цисса точки перегиба. Находим y(0) = 0.

(−∞;−3)

−3

(−3; −1)

−1

(−1;0)

(0;∞)

−

y′

–

y′′

–

∩

max

∩

перегиб

194

Лекции 1 - 2

График y =

2 (x +1)2

имеет вид:

Пример:

Исследовать функцию

y =

и построить её график.

−1

Решение:

1). Функция определена всюду, кроме точек x = ±1 .

Точки пересечения графика с координатными осями:

= 0 x = 0 ;

x2 −1

о ямиantigtu.

y = 0 - точка пере ечения

2). Функция нечетная,

f (−x)= − f (x), график симметричен относитель-

но начала координат, достаточно исследовать функцию при x ≥ 0 .

3). Точка x =1 являетсяст чкой разрыва 2-го рода, график функции имеет

вертикальную асимптоту x =1,

lim

f (x)= −∞, lim

(x)= +∞.

x→1−0

x→1+0

Выяс им, существуют ли наклонные асимптоты. Вычислим пределы:

k = lim

(x)

= lim

=1 ;

, т.е.

y = x яв-

b = lim

− x

= lim

= 0

−1

x→+∞

x→+∞ x

x→+∞

x→+∞ x

ляется пр вой наклонной асимптотой (и левой, так как при операции

симметрии прямая переходит сама в себя).

4). Находим производную:

y′ =

x2 (x2 −3)

. Знак производной определя-

(

−1

)

ется знаком x2 −3 . При x >

3 y′ > 0 , а при 0 < x <1 и 1 < x <

y′ < 0 .

Интервал возрастания - ( 3;∞); интервалы убывания

(0;1)

и (1; 3 ).

В области определения функции производная обращается в нуль при

x = 0 и x =

3 .

При x <

′

< 0

, а приx

′

> 0 . Следовательно, точка x =

3 яв-

Скачано

Исследование функций и построение графиков

195

ляется точкой минимума.

Находим значение функции при x =

3 :

y ( 3 )=

( 3 )3

При переходе через критическую точкуx = 0 производная знак не меня-

ет, т.е.

x = 0 не является точкой экстремума.

5). Находим вторую производную y′′ =

2x(x2 +3)

(

x2 −1

. Видим, что y′′ < 0 при

)

0 < x <1, на

интервале

(0;1)

график

функции

выпуклый

вверх. При

x >

y′′ > 0 - график функции выпуклый вниз.

В области определения функции y′′существует всюду;

y′′ = 0 при x = 0 .

Так как при переходе через эту точку y′′

меняет знак,

то

x = 0 есть абс-

цисса точки перегиба.

Находим y(0) = 0.

(0;1)

(1;

3 )

(

3; ∞)

−

antigtu–

y′

–

y′′

–

перегиб

∩

min

График

y =

имеет вид:

x2 −1

Пример:

Скачано

196

Лекции 1 - 2

Исследовать функцию y = 3

2x2 − x3

и построить её график.

Решение:

1). Функция определена при всех x . Для нахождения точек пересечения

с осями записываем уравнения

y = 0 и 3 2x2 − x3 = 0 ; получаем, что ось

Oy пересекается в точке с y = 0 , а ось Ox - в точках

x = 0

и x = 2 .

2). Функция общего вида.

3). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные

асимптоты отсутствуют. Ищем параметры наклонных асимптот.

k = lim

(x)

2x2 − x3

= lim

−1 = −1,

= lim

x→∞

b = lim( 3

2x2 − x3

+ x ) = lim x(1+ 3

−

1 ) =

x→∞

−2

1+ 3

−1

−1 x

= lim

x→∞

−

При вычислении второго предела использовано правило Лопиталя для

раскрытия неопределённо ти типа

antigtu.

Скачано

Итак, у графика есть наклонная асимптота; еe уравнение y = −x + 2 .

4). Нах дим пр изв дную:

y′ =

4 −3x

. Знак производной опреде-

x(2 − x)2

ляется з аком выражения

4 −3x

. Видим, что в области x < 0

′

< 0 , при

0 < x <

y′ > 0

и при x >

y′ < 0 .

Получ ем, что в области x < 0 функция убывает, при 0 < x <

- возрас-

тает и при x >

- убывает.

′

Н ходим критические точки.

= 0

при

x = 3 , y

не существует при

x = 0 , x = 2 .

При переходе через x = 0 знак производной меняется с (-) на (+), т.е. это

точка минимума.

При x = 0 производная не существует, значит, минимум острый.

Исследование функций и построение графиков

197

y(0) = 0.

При переходе через вторую критическую точку

x =

производная ме-

antigtu

няет знак с (+) на (-) , т.е. при

x =

- максимум:

При переходе через x = 2 знак производной не меняется, значит экстре-

мума нет.

5). Находим вторую производную:

y′′ = −

4 (2 − x)

Видим, что y′′ < 0 приx < 0 ; в этой области график выпуклый; y′′ < 0 при

0 < x < 2, т.е. интервал (0;2)

также является областью выпуклости.

При

x > 2

y′′ > 0 , следователь-

но, при x > 2 график вогнут.

Найдём точки перегиба. Вторая

производная не существует при

x = 0 и приx = 2 .

При переходе через первую точ-

ку знак y′′не меняется,

а при

переходе через вторую – меня-

ется.

Скачано

Итак, точкой перегиба являет я

точка

координатами

x = 2 ,

y( 2 ) = 0 .

График y = 3 2x2 − x3 имеет вид:

В результ те изучения м териала, изложенного в этих лекциях,

у студентов должны сформироваться следующие понятия:

то ки разрыва,

асимптоты графика,

экстремумы функции,

точки перегиба.

Студент должен уметь:

применять общую схему исследования функции,

строить графики сложных функций.

Лекции 3 - 4
КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ
В КОМПЛЕКСНОЙ ОБЛАСТИ
antigtu	приме-
Комплексные числа – расширение множества действительных чисел, широкоru	приме-

няющееся в естественных и прикладных дисциплинах. Использование .комплексных чисел позволяет наиболее естественным образом описать многие процессы, в частности, колеба-

тельные. Изучение функций комплексного переменного привело к углублению и расширению знаний о функциях действительных переменных и породило множество мощных вычислительных методов.

3.1. Комплексные числа. Основные определения. Алгебраическая форма комплексного числа

3.2. Изображение комплексного числа на плоскости. Тригонометрическая форма комплексного числа

3.3. Формула Эйлера. Показательная форма комплексного числа 3.4. Действия над комплексными числами

3.4.1. Сравнение, сложение и вычитание 3.4.2. Умножение, деление, возведение в целую степень 3.4.3. Комплексноессопряжение 3.4.4. Извлечение корня

3.5. Комплекснозначная функция действительного аргумента 4.1. Многочлены в комплек ной области. Корни многочлена

4.2. Основная теорема алгебры Скачано4.3. Примеры решения задач

4.4. Разложение рациональных дробей 4.5. Примеры решения задач

3.1. Комплексные числа. Основные определения. Алгебр ическ я форма комплексного числа

О Комплексным ислом называют упорядоченную пару действительных чисел z = (x, y ) со следующими свойствами:

1) два комплексных числа z1 = (x1 , y1 ) и z2 = (x2 , y2 ) равны тогда и толь-

ко тогда, когда x1 = x2 и y1 = y2 ;

2) сумма двух комплексных чисел z1 = (x1 , y1 ) и z2 = (x2 , y2 ) определяет-

ся следующим образом:

z1 + z2 = (x1 , y1 )+ (x2 , y2 )= (x1 + x2 , y1 + y2 ).

Комплексные числа. Многочлены в комплексной области

199

3) произведение двух комплексных чисел z1 = (x1, y1 ) и z2 = (x2 , y2 )

опреде-

ляется следующим образом:

z1 z2 = (x1 , y1 ) (x2 , y2 ) = (x1 x2 − y1 y2 , x1 y2 + x2 y1 )

Действительные числа содержатся в множестве комплексных чисел,

все они являются парами вида

x,0

. В дальнейшем будем обозначать

(x, 0)= x .

(

)

Пары вида (0, y) называются чисто мнимыми числами.

Пара i = (0,1) носит специальное название - мнимая единица. Согласно

свойству 3) i i = (−1,0)= −1.

z = (x, y) можно записать в виде суммы

Каждое комплексное число

действительного числа x = (x,0)

и чисто мнимого числа iy = (0, y):

z = (x, y)= (x,0)+ (0, y)= x + iy .

Действительное

число

x = Re z

называется

действительной

частью

комплексного числа z ,

действительное число

y = Im z называется мни-

мой частью z .

Комплексное число z =0 , если x = Re z =0 и y = Im z = 0 .

Запись z = x + iy называет я

antigtu

алгебраической формой комплексного

числа.

3.2. Изображе ие комплекс ого числа на плоскости.

Тригонометрическая форма комплексного числа

Так как z = (x, y) определяется как пара

действительных чисел, то естественной геомет-

рической интерпретацией является изображе-

ние комплексного

исла точкой М некоторой

плоскости с координ тами (x, y).

Т кую плоскость называют комплексной,

ось

бсцисс - действительной осью, ось орди-

Скачано

нат – мнимой осью. При этом устанавливается взаимно-однозначное соответствие между множеством всех комплексных чисел z = (x, y) и множеством

точек М(x, y) или множеством радиус-векторов OM .

200	Лекции 3 - 4
Введем на плоскости XOY полярные координаты (r, ϕ). Длина вектора
OM называется модулем комплексного числа z и обозначается	z	или r :

z = r = OM = x2 + y2 .

оси OX называют аргументом комплексного числа z: ϕ = Arg (z). Угол ϕ определяется неоднозначно, с точностью до слагаемого 2πk . Удобно рабо-

тать с приведенным аргументом ϕ = arg (z), 0 ≤ϕ < 2π (либо −π ≤ϕ <π ).

Для числа z =0 +i0 аргумент не определён. При этом аргумент комплексного числа определяется следующим образом:

Угол ϕ между радиус-вектором OM и положительным направлением
antigtu	.	ru

						y	, если x > 0,
			arctg
			arctg			x
						x
						y
						y	+π, если x	< 0, y > 0,	(для 0 ≤ϕ < 2π ).
			ϕ = arctg
			ϕ = arctg			x
						x
						y	−π, если x	< 0, y < 0.
			arctg
			arctg			x
						x	с
							с		решают систему уравнений
Практически, для определения ϕ = rg( z )									решают систему уравнений
cosϕ =	x	,	sinϕ =	y	и изображают			z вектором,	чтобы определить, в каком
cosϕ =	r	,	sinϕ =		и изображают			z вектором,	чтобы определить, в каком
	r			r

квадранте лежит точка. Так как x = r cosϕ , y = r sinϕ , то комплексное число z = x + iy можно записать в следующем виде: z = r(cosϕ +i sinϕ) , которое называют тригонометрической формой записи комплексного числа.

3.3. Формула Эйлера. Показательная форма комплекс ого числа

Используя формулу, полученную Эйлером: eiϕ = cosϕ +isinϕ (которая будет доказана позже, при изучении теории рядов), можно получить еще одну, показательную, форму комплексного числа: z = r eiϕ .

Комбинируя eiϕ = cosϕ +isinϕ и e−iϕ = cos(−ϕ)+ isin (−ϕ)= cosϕ −isinϕ ,

можно получить выражения cosϕ =	eiϕ + e−iϕ	, sinϕ =	eiϕ − e−iϕ	.
	2		2i
Скачано

Комплексные числа. Многочлены в комплексной области

201

Пример:

Записать число z =

2 −i 2

в различных формах. Дать геометрическую

интерпретацию.

antigtu

Решение:

Алгебраическая форма: z =

2 −i

;

тригонометрическая

форма:

r =

= 2 + 2 = 2 ;

7π

= cos

, −

= sin

ϕ=−π

7π

откуда ϕ = arg( z ) =

r=2

z =

−i

7π

+isin

7π

= 2 cos

;

7π

показательная форма: z = 2e 4 .

3.4. Действия над комплексными числами

Операции в арифметической форме производятся в соответствии с усло-

вием

i i =

(−1,0) = −1

обычными

правилами алгебры.

Обозначим

= (x1

, y1 ) = x1 + iy1

z2 = (x2

, y2 ) = x2 + iy2 .

Скачано

3.4.1. Сравнение, сл жение и вычитаниес

Сравнение

чисел

алгебраической

форме:

z1 = z2 , если x1 = x2

и y1 = y2 .

Если числа заданы в триго ометрической или пока-

зательной форме: z1 = r1 (cosϕ1 + i sinϕ1 ) ,

= r (cosϕ

+ i sinϕ

) или z = r eiϕ1 ,

= r eiϕ2

то z1 = z2 , если r1 = r2 ,

ϕ1 =ϕ2 + 2πk; k Z .

Сложение в алгебраи еской форме:

z1 + z2 =

(x1 + x2 , y1 + y2 )= (x1 + x2 )+ i(y1 + y2 ).

Вычит ние определяется как действие, обратное сложению: пусть z = z1 − z2 ,

тогда

z1 = z + z2 , z1 = x1 + iy1 = x + x2 + i(y + y2 ),

xx2 − yy2 = x1xy2 + x2 y = y1

202

Лекции 3 - 4

откуда

z1 − z2 = (x1 − x2 )+ i(y1 − y2 ).

С геометрической точки зрения сложение (вычитание) комплексных чисел

antigtu

равносильно сложению (вычитанию) изображающих их векторов

3.4.2. Умножение, деление, возведение в целую степень

Умножение в алгебраической форме:

z1 z2 = (x1 + iy1 )(x2 + iy2 ) = x1 x2 + ix2 y1 + ix1 y2 + i2 y1 y2 =

=(x1x2 − y1 y2 )+ i(x1 y2 + x2 y1 ).

В тригонометрической форме:

z1 z2 = r1 r2 (cosϕ1 + i sinϕ1 ) (cosϕ2 +

s nϕ2 ) =

= r1r2 (cosϕ1 cosϕ2 - sinϕ1sinϕ2 + i( s nϕ1 cosϕ2 + cosϕ1sinϕ2 ) =

т.е.

= r1r2 (cos(ϕ1 +ϕ2 ) + i sin(ϕ1 +ϕ2 )) ,

z1 z2 = r1 r2 (cos(ϕ1 +ϕ2 ) + i si

(ϕ1 +ϕ2 )).

В показательной форме:

= r r ei(ϕ1 +ϕ2 ) ,

z = r eiϕ1 ,

= r eiϕ2

, z z

= r r eiϕ1

eiϕ2

т.е. модуль произведения комплексных чисел равен произведению модулей, а

аргумент – сумме аргументов сомножителей.

Деление определяет я как дей твие, обратное умножению:

Скачано

z =

(x , y )

= (x, y),

1 1

(x2 , y2 )

откуда z1 = z z2 .

Запишем соответствующую ф рмулу для алгебраической формы комплексного числа:

z1 = z z2 = (x1 , y1 )= (xx2 − yy2 , xy2 + x2 y),

откуда получаем систему двух линейных уравнений с двумя неизвестными:

Решаем, используя формулы Крамера:

-y2

∆ = x22 + y22 ≠ 0; x =

; y =

x22 + y22

z1		=	x1 x2 + y1 y2			+ i	x2 y1 − x1 y2			.
z			2	+ y	2		2	+ y	2
	2		x		2		x		2
			2				2

= r2 е

203

Комплексные числа. Многочлены в комплексной области

В тригонометрической форме:

[cos(ϕ1 −ϕ2 ) + i sin (ϕ1 −ϕ2 )] ,

antigtu

в показательной форме:

i( ϕ1 −ϕ2 )

т.е. модуль частного комплексных чисел равен частному модулей, а аргумент

– разности аргументов делимого и делителя.

Возведение в целую степень выводится на основе обобщения операции умножения:

z = r(cosϕ + i sinϕ ) ,

z2 = z × z = r2 (cos 2ϕ +

s n2ϕ ) ;

zn = z × z...× z = r2 (cos2ϕ +isin2ϕ) z × z...× z = rn (cos nϕ + i sin nϕ) ;

n-2

zn = rn (cos nϕ + i sin nϕ) ;

z = reiϕ , zn = r neinϕ .

еinϕ = cos nϕ + isin nϕ , с другой стороны:

Сравним последние две формулы:

еinϕ = (еiϕ )n = (cos ϕ + i sin ϕ)n (cos ϕ + i sin ϕ)n

= cos nϕ + isin nϕ . Послед-

нее соотношение называется формулой Муавра.

Пример:

Найти z11

, если z =1−i .

Скачано

Решение:

2; arg z = −

( z расположено в IV квадранте).

Тогда z =

2 e−i

4 .

−i11π

11π

= ( 2) e

= 2

cos

+i sin

−

3π

−i sin

3π

−i

+i).

= 2 2

cos

= 2 2

−

= −2

3.4.3. Комплексное сопряжение

Комплексным числом,

сопряженным к z = x + iy ,

называется комплекс-

ное

число

z , отличающееся

от

только знаком мнимой части:

z = x −iy .

Свойства операции сопряжения:

1°.

= z ;

2°.

z = z тогда и только тогда, когда z - действительное число;

204

Лекции 3 - 4

3°.

z1 ± z2

4°.

z1 z2 = z1 z2 ,

antigtu

(z )

5°.

(z2 )

6°.

z z = x

+ y

Докажем некоторые соотношения.

В алгебраической форме: z = x +iy, z = x - iy .

Вычислим:

а)

z + z = (x +iy)+ (x −iy)= 2x , следовательно,

z + z = 2x ; z − z = 2iy ;

б)

zz = (x +iy)(x −iy)= x2 + y2 , следовательно:

z z = x2 + y2 .

Тогда

z z

(x1x2 + y1 y2 )

+ i(x2 y1

− x1 y2 )

x22

+ y22

z2 z2

x1x2 + y1 y2

+ i

x2 y1 − x1 y2

+ y2

x2 + y2

В тригонометрической форме:

z =

(cosϕ +isinϕ) ;

(cosϕ −isinϕ) =

(cos(−ϕ) + isin(−ϕ)) .

Скачано

В показательной форме:

z =

eiϕ ,

z =

e−iϕ .

Геометрически - к мплексн е с пряжение есть операция сим-

метричного отраже ия вектора, соответствующего числу z от-

носительно действитель

ой оси.

Вывод: пользуясь алгебраической формой комплексного числа, можно

производить опер ции сложения, умножения, вычитания по обычным правилам умножения многочленов. При делении комплексных чисел эффективно использов ть прием умножения числителя и знаменателя на число, сопряженное знаменателю.

Свойства опер ций сложения и умножения:

1°. z1 + z2 = z2 + z1 ,

2°. (z1 + z2 )+ z3 = z1 + (z2 + z3 ), 3° z1z2 = z2 z1 ,

4°. (z1z2 )z3 = z1 (z2 z3 ),

5°. (z1 + z2 )z3 = z1z3 + z2 z3 .

Комплексные числа. Многочлены в комплексной области

205

Пример:

Найти

и arg z для числа: z =1+i .

z=1+i

Решение:

= arctg1 = π

z =1+i ,

1 +1 =

2 , α = arctg

Здесь k может принимать

в е возможные целыеantigtuзначения.

3.4.4. Извлечение корня

Определяется как действие обратное возведению в степень.

Число b называется корнем n-ой степени из числа z

и обозначается b = n z ,

если bn = z .

Пусть z = reiϕ ,

а b = ρeiϕ

и r, θ

известны. Найдемρ,θ .

Два комплексных

числа равны bn

= z , если равны их модули

ρ = r ρ = n

и аргументы от-

личаются на

2kπ .

nθ =ϕ + 2kπ

ϕ + 2kπ ,

n reiϕ

= n r ei

ϕ+2кπ

или

2π

окончательно n

reiϕ = n r ei( n +k n ) .

Скачано

Различных (неодинаковых) значений корней будет ровно n, и они будут

соответствовать значениям k = 0, 1, 2, …, n-1.

b = n

r ei n

, k = 0 ,

2π

b = n

r ei( n

n ) , k =1,

2π

b = n

r ei( n

+2 n ) , k = 2 ,

= n r ei

+(n−1)

2π

( n

) , k = n −1.

n−1

Если же, например, k = n , то

2πn

) = n r ei(

b = n

r ei( n

+2π ) = n rei n ei2π =

= n rei n 1 = b → b = b ,

аналогично bn+1 = b1 и т.д.

Вывод: корень n-й степени из комплексного числа имеет n различных значений.

206

Лекции 3 - 4

Числа b0 ,b1 ,...,bn−1

имеют

одинаковый модуль,

так

как аргументы

отличаются, следовательно, значения корня будут изображаться точками

на окружности.

Пример:

Вычислить и изобразить на комплексной плоскости

4 i

Решение:

Запишем число i

в показательной форме:

i π

πk

w = i = e

2 ;

z = 4 w

+2πk

= e4 2

= e

2 .

Возможно четыре различных значений корня, соответ-

ствующих

k =0,1, 2, 3 :

z = e 8 , (k = 0) ,

= ei(

= ei( 8 +

2 ) , (k =1) ,

8 +π ) , (k = 2) ,

= e ( 8

+3 2 ) , (k = 3) .

получен

из корня

поворотом на

против часовой стрелки,

z2 из z0

поворо-

том на π и т.д.

Пример:

Вычислить

6 1 + i

3 ; изобразить схематично зна-

чения корня на комплексной плоскости.

Решение:

iπ

antigtu

w =1 + i 3 = 2e 3 ;

+ 2πk

= 6 2 = 2

; θ =

; k = 0,1, 2,3, 4,5 .

Начальный аргумент при k = 0 равен θ =

аче ия кор я:

7π

13π

z = 6 2 ei

, z

= 6

2 ei

18 , z = 6 2 ei

18 ,

19π

25π

2 ei

31π

= 6 2 ei 18

, z = 6

2 ei 18 , z = 6

18 .

Соответствующие 6 точек располагаются в вершинах правильного шести-

угольника на окружности радиусом 6 2 .

Пример:

Решить уравнение z 2

+ z +1 = 0 .

Используя

формулу

для

решения

квадратного

уравнения

полагая

−1 = i , имеем: z

= −1 + i

3 ,

= −1 −i

3 .

Рассмотренное уравнение имело вещественные коэффициенты. Пусть ко-

эффициенты комплексные.

Скачано

Комплексные числа. Многочлены в комплексной области

207

Пример:

Решить уравнение z 2

+ (−3 + i2)z + 5 −i = 0 .

По формуле квадратного уравнения

z = −( −3 + 2i ) + ( 2i −3 )2 −4( 5 −i )

= 3 −2i + −15 −8i

Число, стоящее под знаком квадратного корня, можно было бы записать

в показательной форме, а затем по известному правилу извлечь из него

корень. Однако можно поступить иначе. Положим

−15 −8i = x + iy.

Возводим обе части в квадрат и находим

−15 −8i = x2 − y2 + 2ixy , откуда x2

− y 2 = −15 ; 2xy = −8 .

Эта система имеет решения: x1 =1, y1

= −4, x2 = −1, y2 = 4; поэтому

z = 3 − 2i + (1 − 4i) = 2 −3i, z

= 3 − 2 + (−1 + 4 ) =1 + i.

antigtu

3.5. Комплекснозначная функция действительного аргумента

Если каждому действительному t ставится в соответствие комплексное z,

то z = z(t) называют комплекснозначной функцией действительного

аргумента.

z = eiϕ -

комплекснозначная функция действительного аргумента ϕ . В

алгебраической форме:

z(t) = x(t) + i y(t) . Так как z(t)

соответствует вектору

с координатами х(t) и

z(t)

эквивалентно заданию

y(t) , то задание функции

вектора функции скалярн го аргумента.

Теория комплексн значных функций скалярного аргумента совпадает с

теорией векторной фу кции скалярного аргумента.

′

z'(t) = x (t) + iy (t) - формула дифференцирования комплекснозначной функ-

ции.

4.1. Много лены в комплексной области. Корни многочлена

Многочленом называется функция вида:

P ( z ) = a zn

+ ... + a

n−2

z2 + a

n−1

z + a

; a ≠ 0 ,

где n – степень многочлена (n – натуральное), а коэффициенты a0 ,..., an

могут быть как действительными, так и комплексными, z – комплексная

переменная. При a0 =1 многочлен называется приведённым.

Рациональной дробью называется отношение двух многочленов

Скачано

208

Лекции 3 - 4

P ( z )

b zm + b zm−1

+ ... + b

z + b

m−1

m .

P ( z )

a zn + a zn−1

+ ... + a

n−1

z + a

При m < n дробь называется правильной, при m ≥ n

дробь называется не-

правильной.

antigtu

Неправильную дробь всегда можно разложить на сумму многочлена и правильной дроби; вид многочлена находится при делении «уголком» или по схеме Горнера. Свойство деления можно записать следующим образом:

Pm ( z ) = Ql ( z ) + Rp ( z ) . Pn ( z ) Pn ( z )

Здесь Ql ( z ), Rp ( z )- многочлены степени l и p соответственно;

Ql ( z ) - частное (целая часть дроби); l ≤ m l + n = m , Rp ( z ) - остаток ( p < n ).

Пример:
	2z3 +3z2 +6z −3	= 2z +1	+	3z −4	.
	z2 + z +1	= 2z +1	+	z2 + z +1	.
	z2 + z +1			z2 + z +1

Если Rp ( z ) =0

Pm( z )

Pm( z ) = Pn

( z ) Ql ( z ) . В этом случае

= Ql ( z ) ;

Pn ( z )

говорят о делении нацело.

Корнем многочлена Pn( z ) называют число z0 , удовлетворяющее

уравнению Pn( z ) =0 или в развёрнутом виде.

a zn

+ ... + a

n−2

+ a

n−1

z + a

= 0; a ≠ 0 .

Данное урав е

ие является алгебраическим уравнением n-й степени.

Теорема Безу.

Остаток, получаемый при делении Pm( z )на (z-a), равен

Pm( a )

Доказ тельство:

По условию Pn (z) = P1 (z) = z-a . По основному свойству: Ql (z) = Qm-1(z) ,

Rp ( z ) = R0 ( z ) = R0 . Тогда Pm( z ) = Qm−1( z ) ( z − a ) + R0

Положим z = a , тогда получим равенство Pm (a) = R0 , что и требовалось

док з ть.

Для того чтобы многочлен Pn( z ) делился на выражение (z-a) без остат-

а, необходимо и достаточно, чтобы число z = a было корнем этого мно-

гочлена. Таким

образом,

если

z = z0

- корень Pn( z ), то

Pn( z ) =( z − z0 ) Qn−1( z ) . Другие корни Pn( z )

следует искать из уравне-

ния: Qn-1 (z) = 0 и т.д.

Скачано

Комплексные числа. Многочлены в комплексной области

209

Пример:

Проверить, что z =1 является корнем многочлена P (z) = z3

+ z 2 + 3z −5

и найти другие корни многочлена.

Решение:

P3 (1) =1 +1 + 3 −5 = 0 , то

z =1 является корнем

Так

как

многочлена

P3 (z) и многочлен P3 (z)

делится на

z −1 без остатка.

−

z 3

+ z 2

+ 3z − 5 | z −1

z 3

− z 2

z 2 + 2z

+ 5

− 2z 2

+ 3z

P (z) = (z −1)(z2 + 2z + 5).

2z 2

− 2z

−5z − 5

5z − 5

Если P ( z ) =( z − z )k

Q ( z ) , где Q antigtu( z ) ≠ 0, то z называют корнем

Для отыскания

других

корней многочлена

решим

уравнение

z 2

+ 2z + 5 = 0 :

z = −1 ±

1 −5 = −1 ± 2i.

Итак,

многочлен

(z) = z3 + z 2

+ 3z −5

имеет один действительный корень

=1 и два

комплексно-сопряженных корня z2

= −1 + 2i , z3 = −1 − 2i.

n−k

n-k

кратности к многочлена P n (z) .

Скачано

Пример:

+3z

3z +1 = (z +1)(z +1)(z +1) = (z +1)

;

P 3 (z) = z

= −1- к рень кратн сти 3.

4.2. Основн я теорема

лгебры

Любой много лен P n( z ) при n ≥1 имеет хотя бы один корень (действи-

тельный или комплексный).

1). Каждый много лен Pn ( z ) имеет ровно n корней, если каждый корень

счит ть столько раз, какова его кратность.

2). (с учетом теоремы Безу) Всякий многочлен n-й степени разлагается

на n линейных множителей вида z − zk

и множитель, равный коэффици-

енту при zn . P ( z ) = a

( z − z

)( z − z )...( z − z ) .

Для случая кратных (повторяющихся) корней формула группируется следующим образом:

210							Лекции 3 - 4
P ( z ) = a	n	( z − z	)k1 ( z − z	2	)k2 ...( z − z	m	)km	(*)
n	n	1		2		m
здесь zi – корни кратности ki , i =1,2,…,m, k1 + k2 + ...+ km = n
Рассмотрим случай многочленов с действительными коэффициентами.

Т Если многочлен Pn ( z ) с действительными коэффициентами имеет ком-
	плексный корень	z0 = α +iβ			ru
					ru
			кратности к, то он имеет и комплексно-
				.
сопряженный корень z0		=α −iβ той же кратности.		.
			antigtu
			antigtu

Вывод: комплексные корни многочлена с действительными коэффициентами появляются сопряженными парами.

Т Многочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами. Рассмотрим линейные множители вида ( z − zi ) , где zi - действительное

число, и объединим множители вида (z − zl )(z − zl ) , где zl - комплексное

число. Тогда ( z − z	) ( z − z	l	) = z2 − z( z	l	+ z	l	) + z	l	z	.
l		l		l		l		l	l
Но z + z = (α + iβ) + (α −iβ) = 2α,					z z =(α + iβ ) (α −iβ ) =α2 + β2
l l			с		l		l
являются действительными числами, обозначим их p и q соответственно.
Тогда (z − zl )(z − zl ) = z2 + pz + q,						где p, q – действительные числа, а

квадратный трехчлен имеет только комплексные корни и не разлагается на

линейные множители с дей твительными коэффициентами. Таким образом, многочлен Pn (z) с действительными коэффициентами имеет следующее раз-

ложение:

Pn( z ) = a0 ( z − z1 )s1 ( z − z2 )s2 …( z − zi )si ( z2 + p1 z + q1 )k1 …( z2 + p j z + q j )k j ,

где s1 + s2 +…+ si + 2k1 +…+ 2k j = n .

!	Данное выр жение представляет собой произведение множителей двух
	типов:
	типов:
	1). Линейные множители ( z − z )si					, где z		i	- действительный корень крат-
	ности Si .				i			i
	ности Si .						(z2 + pz + q)kj с
2).		Кв др тичные		множители			(z2 + pz + q)kj с			действительными
	коэффициент ми p,		q и отрицательным дискриминантом D = p2 -4q < 0 .
				2		k j				k j
	Данные множители			(z + pz + q)							соответствуют
	Данные множители			(z + pz + q)			= (z		− z j ) (z − z j )		соответствуют
	паре	омплексно-сопряженных корней z j ,z j кратности k j .
Скачано

Комплексные числа. Многочлены в комплексной области

211

Пример:

Разложить на множители P(x) = х3 +1 .

Линейные множители (действительные корни):

= −1 ; х3

+1 делится на

х+1 без остатка,

antigtu

P (х)= х3 +1 = (х

+1)(х2

− х

, у трехчлена действи-

тельных корней нет.

Найдем пару комплексно-сопряженных корней:

x2,3

1± 1-4

1±

−3

1±

−1

1±i

P (x)

= (x +1)

1+i 3

1−i 3

x −

4.3. Примеры решения задач

Пример:

Разложить на множители многочлен

(z) = z 4

+1.

Решение:

Скачано

Очевидно, действительных корней многочлен не имеет, находим ком-

плексные корни:

iπ

i( π+2kπ )

= −1+ 0i = e

;

−1+ 0i = e

; где k = 0;1;2;3.

3π

5π

7π

Кор и м огочле а:

z = ei 4 ; z

= ei

; z

= ei

; z

= ei

П ры z1 , z4 ; z2 , z3

- сопряженные: z 4 +1 = (z − z1 )(z − z4 )(z − z2 )(z − z3 );

объединим поп рно сомножители:

z4 +1 = (z2 − z(z + z

) + z z

)(z2 − z(z

+ z

) + z

) ,

+ z

= cos π

+i sin π +cos 7π

+i sin 7π =

−i

= 2 ,

z1 z4

=1.

Аналогично, z2 + z3

= −

2, z2 z3

=1.

Тогда

P ( z ) = z 4 +1 = ( z 2

2z +1)( z 2

−

2z +1).

212

Лекции 3 - 4

Пример:

Дать геометрическое описание множества всех

комплексной

точек

плоскости, удовлетворяющих условиям:

1 ≤

≤ 5

antigtu

Imz ≤ 0

Решение:

в алгебраической форме z = x + yi , тогда

Запишем

из условия :

1 ≤

+ y

≤ 5

≤ x

+ y

≤ 5

−5 −1 0 1 5

y ≤ 0

≤ 0

Геометрически: нижняя половина кольца с внутрен-

ним радиусом R1

= 1 и внешним R2 = 5.

Пример:

Представить

тригонометрической

показательной

формах числа

= 2 +

2 i; z

= 5 −12i;

= −i.

Решение:

eiϕ1

z = x + iy =

;

= π ,

1 + 1 = 1

= ei

π + i sin π ;

ϕ = arctg

;

= cos

25 +144 =

169 =13 ;

Скачано

ϕ2

= arctg

;

ϕ2

− угол, лежащий в IV четверти.

−

i arctg

−

= 13e

=13 cos arctg

−

+i sin arctg −

;

1 +

0 = 1;

ϕ3 = −

;

z3 = e

−i

= cos

−i sin

Пример:

Выполнить действие:

+ 2

i 9

+ 2i8 +i7

+11

i 2 + 2

Решение:

Поскольку i2

= −1;

=1,... i9

= i,

i8 = +1, i7

= −i.

+ 2

−1 + 2

i9 + 2i8 + i7 +11

i2 + 2

+ 2

−i +11

−1 +

+i −i =

Комплексные числа. Многочлены в комплексной области

213

Пример:

Вычислить 4

2 +

2i .

Решение:

ϕ+2πk

z = 4

; где

k = 0; 1; 2; 3 .

= π ;

= 2 + 2 = 2; ϕ = arctg

ϕ - угол, лежащий в I четверти.

9π

17π

25π

z = 4 2ei

; z = 4 2ei

; z =

4 2ei

; z = 4 2ei

Пример:

Разложить многочлен

x4 + 6x3 + 25x2 + 68x

на множители с действи-

тельными коэффициентами.

Решение:

x1 = 0 . Подбором находим

x2 = −4 , с помощью деления “уголком” по-

лучаем:

x4 + 6x3 + 25x2 + 68x

= x

+ 2x +17; D = 4 − 4 17 < 0 .

x( x + 4 )

Тогда разложение имеет вид :

x4 + 6x3 + 25x2 + 68x = x( x + 4 )( x2 + 2x +17 ) .

Пример:

antigtu

Решить биквадратное уравнение

z4 + 4z2 + 3 =

0 .

Решение :

(

)

= 0 .

z4 + 4z2 + 3 =

z2 +1

+ 3

)(

z1,2 = −1 = 0 ± i ; z3,4 =

с− 3 = 0 ± i 3 .

Пример:
	Разложить м огочлен а квадратные множители при условии, что задан
	один из кор ей.
	x4 +8x3 + 21x2 +8x + 20; x = −4 + 2i .
	Решение:		1
	Решение:
	Поскольку для многочлена с действительными коэффициентами корни
	появляются только сопряженными парами, то			x2 = −4 − 2i . Соответст-
	вующий квадратный трехчлен:
	( x − x )( x − x ) =( x + 4		− 2i )( x + 4 + 2i ) =(( x + 4 )2 − 4i2 ) =
	1	2
	= x2 +8x + 20.
	Делением начального многочлена получаем :
	x4 +8x3	+ 21x2 +8x + 20 =( x2 +8x + 20 )( x2		+1).
Скачано

214

Лекции 3 - 4

Пример:

Найти множество точек комплексной плоскости, удовлетво-

ряющих условию

z −i

=1.

antigtu

Решение:

z −1 = x + iy − i = x + i( y −1) = x2 + ( y −1)2 =1,

x + ( y −1)

=1. Следовательно,

искомое множество со-

стоит из точек окружности единичного радиуса, центр кото-

рой имеет координаты (0;1) .

4.4. Разложение рациональных дробей

Т	Всякую правильную рациональную дробь можно разложить на сумму
	простейших дробей четырех типов:

		A	;	A	;	Bx +C	;	Bx +C	, p2 − 4q < 0 .
				(x - a)k		x2 + px + q		(x2 + px + q)k
		x - a

При этом каждому действительному корню а кратности m в разложении

знаменателя Pn (x) соответствует сумма

+ ...+

x - a

(x - a)2

(x - a)m

Каждой комплексно

кратности m соот-

опряженной паре корней zi ,zi

ветствует сумма

M1x + N1

Mm x + Nm

M 2 x + N2

+ ...+

x2 + px + q

(x2 + px + q)2

(x2 + px + q)m

Коэффицие ты Ai ,Mi ,Ni

аходятся методом неопределённых коэффи-

Скачано

циентов при оди аковых степенях x в числителях после приведения к общему зн мен телю правой части разложения.

Пример:

Разложить на суммы простейших дробей правильную дробь

(

x2 −

1 (x −2)

)

Преобразуем знаменатель, пользуясь формулой разности квадратов:

(

)

− 2)= (x −1)(x +1)(x − 2);

−1

(x −1)

, (x +1)

,(x −2)

;

x −1

x +

x −

(

)

−

1 (x

−

x −1 x +1 x −2

Комплексные числа. Многочлены в комплексной области

x = A1 (x +1)(x −2) + A2 (x −1)(x − 2) + A3 (x −1)(x +1) .

Первый способ нахождения коэффициентов.

Равенство справедливо для любого x , в том числе и для

x= −1: −1 = A2 (−2)(−3)

x = 2: 2 = A3 (1) 3

x =1: 1 = A1 2 (−1)

A = − 1

, A = − 1

, A = 2

Второй способ нахождения коэффициентов.

Многочлены равны, когда равны коэффициенты перед одинаковыми

степенями x.

x2 : A + A + A = 0;

x1 : −A −3A =1;

x0 : −2A +

2A − A = 0

A = − 1

, A = − 1

, A = 2 .

Третий способ:

Комбинация первого и второго способов.

Ответ:

= −

−

2(x −

6(x +1)

3(x − 2)

(

antigtu

)

Пример:

x2 −1

= ?

x(x2 +1) 2

(

Порядок многочлена x

+1 2 в знаменателе равен 5.

)

;

B1x + D1

B2 x + D2

+1)

;

(x2 +1)

(x2 +1)2

x2 −1

A B x + D B x + D

;

x(x2 +1)2

(x2 +1)

(x2 +1)2

x2 −1 = A( x2 +1 )2 +(B1 x + D1 )x( x2 +1) +(B2 x + D2 )x ;

x =0 : A = −1;

x4 : A + B = 0 ;

x3 :D = 0 ;

x2 : 2 A + B + B = 1 ;

x: D1 + D2

= 0;

A = −1, B1 =1, D1 = 0, D2 = 0, B2 = 2 .

x2 −1

= −

(

)

Скачано

215

216

Лекции 3 - 4

Пример:

Разложить

рациональную дробь на сумму простейших,

предварительно

выделив целую часть:

x3 − x +8

x3 −

2x2 + x

Решение:

antigtu

− x +8

− 2x + 4

Разделив «уголком», получим:

=1 +

− 2x

+ x + 4

−

+ x +

Разложим

на

множители

знаменатель:

= −1;

x3 − 2x2 + x + 4

= x

− 3x + 4;

x +1

x3 − 2x2 + x + 4 = (x +1)(x2

− 3x + 4).

2x2 − 2x + 4

Bx + C

= Ax2 − 3Ax + 4 A + Bx2 + Bx + Cx + C .

(x +1)(x2 − 3x +

x +

x2 − 3x + 4

x2 :

A + B = 2

A =1;

x1 : −3A + B +C = −2

B =1;

4A +C =

C = 0.

Искомый результат:

x3 − x +16

− 2x

+ x + 4

x +1

− 3x + 4

4.5. Примеры решения задач

Скачано

Пример:

Разложить на суммы пр стейших дробей дробь

x3 + x

Реше ие:

З аме атель P (x) = x3 + x , корни x

= 0; x

2,3

= 0 ± i .

(x) = x(x2 +

1).

Bx +C

Ax2

+ A + Bx2 +Cx

x3 + x

x2 +1

x( x2 +1)

Приравниваем числители и коэффициенты при одинаковых степенях x :

10 = Ax2

+ A + Bx2

+ Cx;

x2 : A + B =

=10;

x1 :

C =

B = −10; .

A =10

= 0,

тогда искомое разложение имеет вид:

−

10x

x3 + x

Комплексные числа. Многочлены в комплексной области

217

Пример:

Разложить неправильную дробь на сумму многочлена и простейших

дробей.

antigtu

x4 + 3x3 + 3x2 + 9

9 −9x

x3 + 3x2 + 3x + 9

= x +

(x + 3)(x2 + 3)

9 −9x

Bx + C

(x + 3)(x2

+ 3)

x + 3

+ 3

9 −9x = Ax2 + 3A + Bx2 + Cx + 3Bx + 3C.

x2 : A + B = 0

A = 3;

x1 :C +3B = −9 B = −3;

:3A

C = 0,

+3C = 9

Ответ:

+ 3x3 + 3x2 + 9

= x +

−

+ 3x2 + 3x + 9

x + 3

Пример:

Разложить правильную рациональную дробь на сумму простейших дробей

3x2

(x −1)2 (x2 + x +1)

3x2

Cx + D

(x −1)2 (x2 + x +1)

x −1

(x −1)2

x2 + x +

Ax3 − A + Bx2 + Bx + B + Cx3 − 2x2 + Cx + Dx2 − 2Dx + D

(x −1)2 (x2 + x +1)

Приравниваем коэффициенты :

Скачано

A +C = 0

A =1;

сA −2C + D

= 3

=1;

B +C −2D = 0

= −1;

D = 0.

−A + B + D = 0

Тогда искомое разложе ие

3x2

−

(x −1)2 (x2 + x +1)

x −1

(x −1)2

x2 + x +1

В результ те изучения м териала, изложенного в этих лекциях,

у студентов должны сформироваться следующие понятия:

комплексные исла и формы их записи,

действия над комплексными числами,

многочлены в комплексной области.

Студент должен уметь:

преобр зовывать комплексные числа из одной формы в другую,

сравнивать, складывать, вычитать, умножать, делить комплексные числа,

возводить в целую степень, извлекать корни целых степеней в удобной для

каждого действия форме;

разлагать рациональные дроби на сумму элементарных.

Лекции 5 - 6 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Интегральное исчисление возникло из потребности создать общий метод разыскания

площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся
antigtu	.	ru

еще Архимедом. Систематическое развитие он получил в 17-м веке, в тесной связи с возникшим тогда же дифференциальным исчислением. В данных лекциях рассматривается первая часть задачи – вычисление первообразной как операция, обратная дифференцированию.

5.1. Основные определения 5.2. Свойства неопределенного интеграла

5.3. Таблица основных интегралов 5.4. Методы интегрирования

5.4.1. Непосредственное интегрирование 5.4.2. Замена переменной в неопределенном интеграле 5.4.3. Интегрирование по частям 5.4.4. Возвратное интегрирование

6.1. Интегрирование рациональных дробей
	с∫
6.1.1. Интегрирование простейших дробей
6.1.2. Общая схема интегрирования рациональной дроби
6.2. Интегрирование выражений, одержащих
тригонометриче кие функции
6.2.1. Интегралы, одержащие произведение
Скачано

тригонометрических функций вида ∫sinm xcosn xdx . 6.2.2. Интегралы вида cosαxcosβxdx;

∫cosαx sinβxdx; ∫sinαxsinβxdx.

6.3. Интегрир вание иррациональных выражений 6.3.1. Ли ей ые иррациональности 6.3.2. Дроб о-ли ейные иррациональности 6.3.3. Квадратич ые иррациональности - тригонометрические подстановки

6.3.4. Интегрирование дифференциальных биномов 6.3.5. Метод неопределенных коэффициентов для интегрирования иррациональностей 6.3.6. Подстановки Эйлера

Пример:

(x)= x2

f (x)=2x, (-∞,∞) ,

219

Неопределенный интеграл

5.1. Основные определения

Функция F (x) называется первообразной для функции f (x)

на интер-

вале (a, b), если F (x)

дифференцируема на

(a, b) и F′(x) = f (x) .

(

)

f (x)=cos(x), (-∞,∞) ,

antigtu

F (x)= sin x

F (x)=

f (x)= =

(0, ∞)

Если F1 (x)

и F2 (x)

– две первообразные для функции f (x) на интерва-

ле

(a, b),

то

они

могут

отличаться

лишь

на

постоянную,

т.е. F1 (x)= F2 (x)+ C , где C – постоянная.

Доказательство:

Положим Φ (x)= F1

(x)− F2 (x).

′

(x)

′

следовательно,

по

теореме

= F1 (x)− F2 (x)= f (x)− f (x)= 0 ,

Лагранжа Φ (x)= C .

F (x)+C ′ = F′(x)+C′ = f (x)+ 0 = f (x).

Скачано

f (x), то любая ее

Если

F (x)

– одна из первообразных для функции

первообразная имеет вид: Φ(x)= F (x)+ C , где C – постоянная.

Совокупность всех

перв

бразных для

функции

f (x)

на

интервале

(a, b)

называется

еопределенным интегралом от функции

f (x) и

обозначается символом ∫ f (x)dx , где ∫ – знак интеграла,

f (x)

– подын-

тегральн я функция, f (x)dx – подынтегральное выражение.

Теорема об интегрируемости непрерывных и монотонных функций

Если

f (x)- непрерывна или кусочно-монотонна на [a,b], то она интег-

рируема на [a,b].

220 Лекции 5 - 6

5.2. Свойства неопределенного интеграла

	Из определения следует, что неопределенный интеграл обладает сле-
дующими свойствами:										ru
1)	dF (x) = f (x)	dx ;								.
2)	∫dF (x)= F (x)+ C ;
3)	Cf (x) dx = C		∫	f (x) dx , где C					– постоянная;
	∫		∫
4)	f (x)± g (x) dx =				∫	f (x)	dx ±	∫	g (x) dx ;
	∫				∫			∫

Если

∫ f (x)dx = F (x) + C , то ∫ f (ax + b)dx =

1F (ax + b)

+ C .

(Доказательство свойства 5 проведем позднее).

5.3. Таблица основных интегралов

∫0dx = С,

∫dx = x +C

∫

= arcsin

+C,

2 − x2

∫xα dx =

xα+1

+C ( α ≠ -1)

∫

= ln

x +

− a

α +1

2 − a

∫x

-1

dx = ∫

+ C

antigtu

x = ln

∫

= ln (x + x2 + a2

)+ C

+ a

∫a

+ C, a >0, a ≠ 1

ln a

∫

+ C (a ≠ 0)

= a arctg

∫exdx = ex

+ C

a2 + x2

∫shx dx = chx + C

∫sin xdx = −cos x +C

∫chx dx = shx + C

∫cos xdx = sin x + C

∫

= thx +C

∫

= tg x +C

ch2 x

cos

∫

−cthx +C

∫

= −ctg x +C

sh2 x

sin

∫

x + a

x − a

− x

Скачано

Неопределенный интеграл

221

Производная любой элементарной функции сама является элементарной

функцией. Интегралы от некоторых элементарных функций не выража-

ются через элементарные функции, они называются неберущимися.

Пример:

∫e−x 2 dx – неберущийся интеграл.

5.4. Методы интегрирования

5.4.1. Непосредственное интегрирование

Отыскание неопределенных интегралов с помощью свойств интегралов,

таблицы интегралов и алгебраических преобразований подынтегральной

функции называется непосредственным интегрированием.

Пример:

∫2

2 x

)

dx =

(2250)x

+ C

dx = ∫(2 3

dx = ∫(2250)

ln 2250

2) ∫(x5 + x7 +8 x )dx =

8x3/ 2

+C =

16x3/ 2

+C.

3/ 2

antigtu

5.4.2. Замена переменной в неопределенном интеграле

Пусть функция

x =ϕ(t )

пределена и дифференцируема на некотором

множестве {t}

и пусть {x}

– множество всех значений этой функции.

Пусть для фу кции

f (x)

существует на множестве {x}

первообразная

функция F (x), т.е.

∫ f (x)dx = F (x)+ C . Тогда всюду на множестве {t}

для функции

f ϕ

(t ) ϕ′(t )

существует первообразная функция, равная

(

))

(

)

(

))

, т.е.

∫

f ϕ

′

dt = F

+ C .

(

)

Доказательство:

Пусть F′(x)= f (x), ∫ f (x)dx = F (x)+C . По правилу дифференцирова-

ния сложной

функции

F ϕ(t ) =

dF (x)

dx =

f ϕ

(t ) ϕ′(t ), значит,

∫ f ϕ

(t ) ϕ′(t )dt = F (ϕ(t ))

+ C , что и требовалось доказать.

Скачано

222

Лекции 5 - 6

Пример:

Пусть ∫ f (t )dt = F (t )

+C .

∫

antigtu

2t dt

f (ax)dx =

t = ax, x

, dx =

∫

f (t )dt =

= a F

(t )+C

= a F

(ax)+C ,

t = x +b,

∫ f (x +b)dx =

= t −b,

=∫ f (t )dt = F ( )+C = F (x +b)+C ,

dx = dt

= ax +b,

∫ f (ax +b)dx =

∫ f ( )

F ( )+C =

F (ax

+b)+C .

x =

−

dx =

Пример:

1). ∫sin (8x − 2)dx = −

1 cos (8x − 2)+ C ;

t =

−1,

x x −1dx =

x = t2 +1,

(

+1 t 2t dt =

)

Скачано

2 t5 +

2 t3 +C =

= 2∫(t4 +t

2 )dt

(x −1)5 +

(x −1)3 +C .

x = 2t,

3) ∫

∫

t =

= ∫

= tg t + C = tg

+ C .

+ cos x

cos

dx = 2dt

Частным случ ем

з мены

является

преобразование

подынтегральной

функции, связ нное с подведением под знак дифференциала части по-

дынтегральной функции.

В этом слу ае замена носит характер переобозначения.

Пример:

xdx

12 d (x2 +1)

t = x2 +1

∫ x2 +1

∫

x2 +1

{

}

= 12 ∫dtt = 12 ln

+C = 12 ln (1+ x2 )+C .

Неопределенный интеграл

2) ∫

∫(5x −2)−1/ 2 dx =

∫(5x −2)−1/ 2 d(5x −2)=

5x −2

={t = 5x − 2}

∫t−1/ 2dt = 1

t1 / 2

+C = 2

5x − 2 + C

= − 9 (1 − x)

+ 2 (1 − x)

− 11 (1 − xantigtu) +C .

3) ∫

sin x cos xdx =∫

sin xd sin x = {t = sin x} = ∫t 2 dt =

+C =

= 2 (sin x)2

+C .

Дополнительные примеры:

Пример:

∫tg x dx = ∫

sin x

u = cos x

= −∫

= −ln

+C = −ln

cosx

cos x

du = −sin x dx

Пример:

= 1 − x, x = 1 −t,

∫(2x +3)

(1 − x)

dx =

dx = −dt,

= −∫(5 −

2t )

t8 dt =

2x +3 = −2t + 5

= −∫(25t8 −20t9 +4t10 )dt = −

9 +

t10 −

t11 =

dxс

Скачано

Пример:

t = x +

∫sin x + cos x

∫

dt = dx

sin x +

+C .

Пример:

∫1 − sinx

x = ∫

dx − ∫ sin x x dx .

1 )

2 )

1) ∫

dx = ∫x−1/ 2dx = x1/ 2

+C ;

1/ 2

sin

x = t,

2) ∫

= ∫sin t 2dt = 2cost + C = 2 cos

x + C .

dx =

∫1−sinx

x dx = 2

x + 2cos

x +C .

223

+C .

224

∫

1−t

∫ t −1

Лекции 5 - 6

Пример:

+ e

(1+e

t = e

∫

dx = ∫

dx =

1−e

−e

= e

1+t

antigtu

dt = −

dt = −{t + 2ln

−1

}+C = = −e x − 2 ln

e x −1

+C .

Пример:

t = ln (tg x),

ln (tg

1 dx

∫

dx =

sin 2x

cos2

s n x cos x

2dx

= 1 dt

sin 2x

1∫t dt = t2 +C = 1 ln2 tg x +C .

24 4

5.4.3. Интегриров ние по частям

Пример:

∫

cos x dx

= sin x,

= ∫

esin x −1

= cos x dx

et −1

домножим и разделим чи литель

и знаменатель на e

и на 2

= 2∫

2et

−1

u =

−1

= u2 +1,

dt = 2∫

= 2∫

2 et −1

= 2arctgu +C =

du =

−1

= 2arctg

esin x −1 +C .

Пример:

ln(arccos x)dx

t = ln(arccos x)

∫

1− x2 arccos x

dt = arccos x

−

1− x

= −∫t dt = −

+ C = −

1 ln2

(arccos x)+ C .

Скачано

d (u v)= (u v)′dx = (u 'v + v'u)dx = u 'vdx + v'udx = vdu +udv ; d (uv)= udv + vdu ; udv = d (uv)− vdu ; ∫udv = ∫d (uv)− ∫vdu ;

∫udv = uv − ∫vdu - формула интегрирования по частям.

Неопределенный интеграл	ru	225

Эта формула используется в тех случаях, когда новый интеграл проще исходного.

В интегралах вида ∫Pk (x)ex dx ; ∫Pk (x)sin x dx ; ∫Pk (x)cos x dx за

обозна-

чается многочлен порядка k Pk (x) ;

Пример:

u = x

dv = sin xdx

∫x sin xdx =

= dx v = −cos x

= -x cos x + ∫cos xdx = −x cos x +sin x +C .

Формулу интегрирования по частям можно применять повторно.

Пример:

u = x

dv = cos x

∫x2 cos x dx =

du = 2xdx

v = si

= x2 sin x − 2∫xsin x dx =

u = x

dv = sin x dx

v = −cos x

= x2 sin x −2 (−x cos x − ∫(−cos x)dx)=

du = dx

antigtu

= x2 sin x + 2x cos x −2sin x +C .

Пример:

u = x dv = dx 2x

x 2x dx =

x 2

−

dx =

x 2

−

+C .

∫

du = dx

v =с

ln2

∫ln2

ln2

(ln2)

ln2

Пример:

u = x

dv = sh x dx

= x ch x − ∫ch x dx = x ch x −sh x +C .

∫x sh x dx =

v = ch x

du = dx

В интегр л х вида

∫

(x)ln x dx

∫

Pk (x)arcsin x dx ,

∫

Pk (x)arccos x dx ,

Скачано

∫Pk ( x )arctg xdx , ∫Pk ( x )arcctg xdx за u обозначается логарифм или обратная тригонометри еская функция.

Пример:
	u	= arctg x, dv					= dx
				dx				=
∫arctg x dx =				dx				=
	du =					, v = x
	du =		1	+ x	2	, v = x
			1	+ x
xarctgx − ∫	xdx	= xarctgx − 12 ln (1+ x2 )+C
xarctgx − ∫	1+ x2	= xarctgx − 12 ln (1+ x2 )+C

226

= −cos xln(tg x)−∫(−cos x)

= −cos xln(tg x)+ ∫

=ru

Лекции 5 - 6

Пример:

u = ln(tg x)

dv = sin x dx

∫sin x ln(tg x)dx =

= −cos x

du =

tg x

cos

tg x

cos2 x

sin x

= −cos xln(tg x)+ln

+C .

5.4.4. Возвратное интегрирование

antigtu

∫

Так называемое

возвратное интегрирование

применяется при вычис-

лении интегралов вида:

∫eax cosbx dx ,

∫eax sin bx dx ,

∫cos(ln x)dx ,

∫sin (ln x)dx

и подобных.

Пример:

∫eax sin bx

dx .

Обозначим I = ∫eax sin bx dx . Тогда

u = e

dv = sin bx dx

eax sin bx dx =

cos bx

du = ae

v = −

Скачано

∫e

= −

cos bx +

cos bx dx = −

cos bx +

I1 .

Полученный интегралсI

возьмем по частям:

u = e

dv = cos bx dx

∫

cos bx dx =

= −

cos bx +

sin bx

du = aeax dx

v =

ax sin bx

sin bx

−

sin bx dx

= −

cos bx +

−

I .

b ∫

То есть

I = −

cosbx +

sin bx

−

I . Выразим отсюда искомый

интеграл I : ∫eax sin bx dx =

eax (asin bx

−bcosbx)

+C .

a2 +b2

6.1. Интегрирование рациональных дробей

Рациональной

дробью

называется

отношение

двух

алгебраических

многочленов

Неопределенный интеграл

227

P (x)

b xm

+ b xm−1

+... + b

x + b

m−1

R (x)

xn + a xn−1

+... + a

−1

x + a

6.1.1. Интегрирование простейших дробей

Правильные дроби четырех типов:

Методы интегрирования про тейших дробейantigtu

;

x − a

, где k – целое положительное число, k >1,

(x − a)k

Ax + B

;

x2 + px + q

Ax + B

, где x2 + px + q – квадратный трехчлен

(x2 + px + q)k

с отрицательным дискриминантом

− q < 0 ,

называют простейшими дробями.

∫

Adx

= A∫

d (x − a)

= Aln

x − a

+ C ;

Скачано

− a

x − a

∫

Adx

=Aln

x − a

+ C .

x − a

(x − a)−n+1

∫

Adx

= A∫(x − a)

−n

d (x − a)

= A

−n +1 + C =

+ C ;

(x − a)n

(1 − n)

(x − a)n−1

∫

Adx

+ C .

(x − a)n

1 − n

(x − a)n−1

Для вычисления интегр ла ∫

Ax + B

разобьем его на два интегра-

x2 + px + q

ла, первый из которых Ia в числителе содержит дифференциал знамена-

теля,

второй Ib

не содержит x в числителе.

Обозн чим u = x2 + px + q du = (2x + p)dx .

∫

Ax + B

2x + p

B − Ap / 2

dx =

∫

dx +

∫

dx ;

x2 + px + q

+ px

+ q

x2 + px + q

228

Лекции 5 - 6

Ia =

+C =

x2 + px + q

+C ,

∫

= B −

antigtu

x + px +

+ q −

Здесь мы выделили полный квадрат в знаменателе и учли, что q −

> 0 .

t = x + p / 2,

Сделаем замену переменной

dt = dx,

= q − p2

/ 4 .

тогда

B − Ap / 2

x + p / 2

Ib =

B −

arctg

+ C .

∫t

+ a

q − p2 / 4

4. Рассмотрим интеграл ∫

Ax + B

dx .

(

+ px + q

)

Аналогично тому, как это было

делано для интеграла 3, заменим

Скачано

+ px + q du = (2x + p)dx .

= x2

Разобьем интеграл на два интеграла:

∫

Ax + B

dx =

∫

2x + p

dx + ∫

(B − Ap / 2)

dx .

(x2 + px + q)k

(x2

+ px + q)k

(x2

+ px

+ q)k

u−k +1

Ia =

∫uk

(1 − k )

+ C = −

(k −1)(x2 + px + q)k −1

+ C .

t = x + p / 2,

∫

Ib = B −

(

)

+ px + q

q − p

/ 4

∫

= B

−

B −

, где

Ik =

(

)

(

)

∫

t2 + a2

+ a2

Неопределенный интеграл

229

Вычислим

u =

dv = dt

+ a

)

+ a

) −a

+ 2k

dt =

∫(t2 +a2 )k

-k2tdt

(t2 + a2 )k

∫

2 + a2 )k +1

du =

v = t

antigtu

найти I3 и т.д.

+ a

)

k +1

+ 2k

∫

− 2ka

∫

(t2 + a2 )k

( 2 + a2 )k +1

Имеем

+ 2kIk − 2ka2 Ik+1 ;

(t2

+ a2 )k

Ik +1 =

2k −1 Ik .

2ka2 (t2 + a2 )k

2ka2

Получена рекуррентная (возвратная) формула, выражающая значение инте-

грала от k +1 - й степени через значение интеграла от k - й степени. Зная
I =		dt	=	1 arctg	t	+ C , по формуле можно найти I		, затем, используя I		,
	∫t2						2		2
1		+ a2		a	a

Скачано

Пример:

∫

x −1

dx .

x2 + x +1

Правильная др бь типа 3.

x −1

2x +1

−1−1/ 2

∫

dx =

t = x

+ x +1

∫

dx + ∫

dx =

+ x +1

= (2x +1)dx

∫

−

∫

x2 + x +1

1 ln

+C = 1 ln

Ia =

+ x +1

+C ,

v = x +1/ 2,

Ib = −

= −

2 ∫

∫v2 + ( 3 / 2)2

(x +1/ 2)2 +3/ 4 dv = dx

= −

arctg

(x +1/ 2) 2 +C .

2x +1

Ответ:

1 ln x2 + x +1 −

3arctg

+C .

230

Лекции 5 - 6

6.1.2. Общая схема интегрирования рациональной дроби ∫

(z)

Pm ( z )

Если дробь

неправильная ( m ≥ n ), то путем деления числителя на

P ( z )

antigtu

знаменатель получают многочлен и правильную рациональную дробь.

P ( z )

= Ql

( z ) +

Rp ( z )

, где Ql

( z ), Rp ( z )- многочлены степени.

l и p со-

Pn ( z )

ответственно;Ql ( z ) - частное (целая часть дроби); l ≤ m, l + n = m

Rp ( z ) - остаток ( p<n ).

Интегрируют многочлен.

3. Находят корни знаменателя правильной рациональной дроби и разлагают знаменатель на квадратичные и (либо) линейные множители с вещественными коэффициентами.

4. Записывают разложение полученной правильной дроби на простейшие.

5. Интегрируют каждую простейшую дробь.

Вывод: интеграл от рациональной дроби выражается через элементарные функции: рациональные дроби, rctg(t) и ln(t) .

Пример:

Вычислить∫

xdx

(

)

−1 (x − 2)

Решение:

Скачано

Разлагаем правильную дробь

(

x2 −1 (x −2)

на сумму простейших:

)

;

(

−1 (x −2)

(x-1)

(x +1)

(x − 2)

)

x = A(x +1)(x − 2) + B(x −1)(x − 2) + C(x −1)(x +1) ;

x =1:1 = −2A, A = − 1 ;

x = −1: −1 = B(−2)(−3), B = − 1

;

x = 2 : 2 = C(1)(3),

C =

2 .

= −

−

(x2 −1)(x −2)

2(x −1)

6(x +1)

3(x − 2)

По свойству линейности:

∫

dx = −

∫

−

(x2 −1)(x − 2)

x −1

x +1

x − 2

= −

1 ln

x −1

−

1 ln

x +

+ 2 ln

x −2

+C .

Пример:

Неопределенный интеграл

Вычислить ∫

+ 2x4 + 2x2 −1

dx .

(

x2 +1

)

x6 + 2x4 + 2x2 −1

- неправильная дробь.

∫

x x2

+1 2

dx =

antigtu

(

)

x2 +1 2

Выделим целую часть:

x6 + 2x4 + 2x2 −1

= x

−1

x(x2 +1)2

x(x2

1)2

Разложим правильную дробь на сумму простейших

x2 -1

B x + D

x(x2 +1)2

= x +

(x2

+1)2 .

x2 -1 = A(x2 +1)2 + x(x2 +1) (B x + D ) + x(B x + D ) ;

x = 0 : −1 = A;

x4 : Ax4 + B x4 =

0, A + B

0, B =1;

x3 : D = 0;

x2 : 2A + B + B

=1, B

x : D1 + D2 = 0, D2 = 0;

x2 -1

x(x2 +1)2

= − x + (x2 +1)+ (x2 +1)2 ;

x6 + 2x4 + 2x2 −1

(

)

Скачано

∫xdx − ∫dxx

∫

dx + 2∫

dx =

2 +1)

(

)

∫

d (x2 +1)

∫

d (x2 +1)

−ln

(x2 +1)

(x2 +1)2

−ln

ln (x2 +1)−

+C .

(

)

231

232	Лекции 5 - 6

6.2.Интегрирование выражений, содержащих тригонометрические функции

	antigtu		.
6.2.1. Интегралы, содержащие произведение тригонометрических
функций вида ∫sinm xcosn xdx .				ru
1. Пусть n и m - четные, неотрицательные числа.		m = 2k , n = 2l, k, l Ν. В

подынтегральной функции степени понижаются посредством перехода к двойному аргументу:

2. Пусть хотя бы одно из чисел n и m - нечетное положительное.

От нечетной степени отщепляется один сомножитель и заносится под зн к дифференци ла d, а оставшаяся подынтегральная функция выражается через фун цию, стоящую под знаком дифференциала по формуле sin2 x + cos2 x =1 .

cos2 x =

1 + cos 2x ,

sin2 x = 1 −cos 2x ;

1 s n 2x .

sin xcos x =

Пример:

xdx =

+cos 2x 2

dx =

cos 2xdx +

cos

2xdx =

cos

∫

4 ∫

∫

4 ∫

sin 2x +

∫(1+cos 4x)dx =

sin 2x +

sin 4x +C .

Пример:

∫sin 2

x cos 4 xdx = ∫(sin x cos x)2 cos2

xdx =

sin 2

2x (1 + cos 2x)

sin

2xdx

sin

2x cos 2xdx =

∫

8 ∫

∫

1 −cos 4x dx =

− sin 4x + C .

∫

sin 2 2xd(sin 2x) =

sin3 2x + C .

−

sin 4x

sin3

2x +C .

Скачано

∫

233

Неопределенный интеграл

Пример:

∫sin3 x cos5 xdx = ∫sin3 x cos4 x cos xdx =

= ∫sin3 x cos4 xd sin x =∫sin3 x (1−sin2

x)2 d sin x =

= (sin3

antigtu

+C ;

x − 2sin5 x +sin7 x)d sin x = 1 sin4

x −

1 sin6

1 sin8 x

1−cos

)

d cos x

∫

sin

dx = ∫

sin

x sin xdx

= −∫

(

−

+C .

cos

2 cos

3. Пусть n и m -

таковы,

что m + n = −2k , где k Ν,

то есть сумма m + n

является четным отрицательным целым. Используется подстановка tgx = t , с

использованием формулы: 1

+ tg2 x =

cos2

3 −5 = −2

sin xdx

sin

tg3 x d (tg x)= tg x

+ C

∫

cos5 x

∫cos3 x cos2 x

∫

tgx = t

			с	∫cosαxsinβxdx; ∫sinαxsinβxdx.
6.2.2. Интегралы вида ∫cosαxcosβxdx;				∫cosαxsinβxdx; ∫sinαxsinβxdx.
Для вычисления следует перейти к				умме функций и сумме интегралов:
Скачано	1	cos (α − β )x + cos (α + β )x ,
cosαx cos βx =	1	cos (α − β )x + cos (α + β )x ,
	2
cosαx sin βx =	1	sin(α − β )x + sin(α + β )x ,
	2
sinαx sin βx =	1 [cos (α − β )x − cos (α + β )x ] .
	2
6.2.3. Универсальная тригонометрическая подстановка
Интегралы вида ∫R(sin x, cos x )dx ,				где R (sin x,cos x)= R(u,v) – рацио-

нальн я функция двух переменных, u = sin x,v = cos x , вычисляются с помо-

щью та			н зыв емой универсальной тригонометрической подстановки
t = tg	x	.	Подстановка t = tg	x	сводит указанный интеграл к интегралу от
	2
			2

дробно-рациональной функции от одной переменной t .

234

Лекции 5 - 6

Рассмотрим:

2tg

2 sin

cos

2 sin

cos

sin x =

;

2 x

+t2

2 x

cos

+ sin

cos

antigtu

−

2 x

cos

−sin

cos

1 −

cos x =

cos

+ sin

2 x

1 +

;

x = 2arctgt, dx =

2dt

1 + 2

Формулы универсальной тригонометрической подстановки имеют вид:

dx =

2dt

; sin x

;cos x

1 −t

; tgx =

;

1 + t2

+ t2

+ t

−t2

1 − t2

2dt

∫R (sin x,cos x)dx = ∫R

+ t2

1 + t2

Скачано

Пример:

2dt

t = tg

dx =

sin x

∫sin x

1+t2

)

2dt 1+t

= ∫

(

= ∫

= ln

+C.

(

)

Пример:

= tg

1 −t 2

cos x =

1 + t 2

∫4 cos x + 3sin x + 5

sin x =

1 + t 2

2dt

1 + t

(t +3)

t +

tg 2 +3

235

Неопределенный интеграл

2dt

= ∫

1 +t2

= ∫

antigtu

1 + t2

+ t

1+ t2

= 2

= −

+C = −

+C.

∫

! Если подынтегральная функция R (sin x, cos x) является четной функци-

ей sin x , cos x , то более эффективной, чем подстановка t = tg

, является

подстановка t = tgx .

Пример:

∫

= ∫

∫

dtgx

a2 sin2 x +b2 cos2 x

cos2 x (a2 tg2 x

+b2 )

x + a2

={t = tgx}

∫

+C =

rctg

arctg a tgx +C

Вообще говоря, перечи ленные методы не исчерпывают всех способов

Скачано

вычисления интегралов от тригонометрических функций.

Пример:

cos x

dx =

sin x = t

∫cos x

∫cos2 x

∫

1 −sin 2

dt = cos xdx

1 1+t +(1−t )

1 dt

∫

1−t2

∫(1+t )(1−t ) dt

∫

1−t

∫

1+t

−

2 ln

t −1

1 ln

1 + t

+ C =

1 ln

1 + t

+ C =

1 ln

1 + sin x

+ C =

t −1

sin x −1

+ cos

x 2

sin

x 2

+ C = ln

+ C.

− cos

sin

∫

= ln

+C.

cos x

236

Лекции 5 - 6

6.3. Интегрирование иррациональных выражений

6.3.1. Линейные иррациональности

antigtu

∫

(2x -1)3

Рассмотрим интегралы вида

∫

x, (ax + b) 1

, (ax +b) 2

,..., (ax +b) k

dx ,

где (ax +b) ni - линейные иррациональности-корни порядка ni, а R(x,y,z,...)

дробно-рациональная функция своих аргументов.

Пусть S

– общий

знаменатель

дробей

m1 ,

, ...,

тогда

подстановка

ts = ax + b

сводит указанный интеграл к интегралу от дробно-рациональной

функции одного аргумента.

Пример:

(2x -1)

t4 +1

dx =

, S

= 4, t

= 2x −1 ; x =

; dx =

dt =

∫

t2 2t

3dt

= 2∫

t2 (t3 +1 −1)

= 2∫t

dt - 2∫

t2 dt

Скачано

dt3

−

∫

-с

+ c = =

(2x -1)4 −

(2x -1)4 +1

+ c .

6.3.2. Дробно-ли ей ые иррациональности

, ... , ax

Интегр лы

вида

R x, ax + b n1

+ b nk dx , где

R( x, y,...)

–

∫

cx + d

+ d

дробно-рациональная функция, вычисляются

при

помощи

подстановки

ax + b = tS , где S

– общий знаменатель дробей

m1 ,..., mk .

cx + d

Пример:

∫

1+ x

(1+ x)2

1-x

= ∫

2 t

(1+ t2 )2 = ∫(t2 +1+t2 −1)2 =

237

Неопределенный интеграл

1 + x

= t

, 1 + x

= t

− xt

x + xt

= t

−1,

x(1

+ t

)

= t

−1,

1-x

−1

+1 − 2

−2

x =

, x =

=1 +

, dx

1 + t2

+ t2

(1 + t2 )2

2a∫R

l2 −u2 )du ;

antigtu

(u,

4tdt

4t2dt

+ t

−1

4t2dt

1-x

= ∫

(2t2 )2

= ∫t2 = − t +c

= -

1+ x

+c .

6.3.3. Квадратичные иррациональности - тригонометрические

подстановки

Интегралы вида ∫R(x,

ax2 +bx + c )dx , где

ax2 + bx + c -

квадратичная

иррациональность, а R( u,v )

- дробно-рациональная функция своих аргумен-

тов, выделением

полного

квадрата

квадратном

трехчлене

и заменой

u = x +

приводятся к интегралу одного из следующих трех типов:

∫R

(u,

2 + u2

)du

;

Скачано

∫R

(u,

2 −l2

)du

к которым применяют триг н метрические подстановки соответственно:

u = l sint

или u = l tht ,

u = l tg t или u = l sht ,

u =

или u = l cht ,

cos t

после чего подынтегр льн я функция сводится к тригонометрической.

Пример:

∫ 5 + 2x - x2 dx = ∫ 5 −( x2 − 2x)dx = ∫ 5 - ( x -1)2 +1 dx = ∫ 6 - ( x -1)2 dx =

x -1 = u

= ∫ 6 - u2 du =

dx = du

u =

sin

t, du

cos t dt ;

t = arcsin

= ∫

6 - 6 sin2 t

cos t dt = 6∫

cos2 t dt = 6

∫(1 + cos 2t)dt =

238

= 3arcsin

6 + 2 2

1−

+ c .

Лекции 5 - 6

= 3t

sin

2t + c = 3 arcsin

x -1

sin 2arcsin

x -1

+ c

x -1

= 3arcsin

sin 2α + c = {sin 2α = 2 sin α cos α} =

antigtu

∫

x -1 3

x -1

(x -1)2

Частные случаи квадратичных иррациональностей

Интегралы вида ∫

выделением полного квадрата в знаме-

+ bx + c

нателе сводятся к табличным.

Пример:

∫

+ 2x +

+ 2x +1+ 4

= ∫

d (x +1)

= ln

x +

+ 2x +5

+ c

( x +1)

+ 2

+ B

Для интегралов вида

dx в числителе выделяется произ-

+ bx + c

водная квадратного трехчлена, тоящего в знаменателе, и интеграл сво-

Скачано

дится к табличному, либо рассмотренному ранее.

Пример:

∫

5x - 3

dx =

2x2 +8x +1

5 (4x +8) -13

(4x +8)dx

= ∫

dx =

∫

-13∫

2x2 +8x +1

∫

d (2x2 +8x +1)

−

∫

2x +8x +1

x2 + 4x + 1

+ 4 −4

2 2x2 +

8x +1 −

∫

d (x + 2)

(x + 2)2 −

2 2x2 +8x +1 −

x +

2 + x2 +

4x +

+ c .

Неопределенный интеграл

239

Пример:

x = atg t,

dx = a

cos

∫(x2 + a2 )3 / 2

2 t

∫

cos

+ a

cos

∫cos t dt

sint +C = ={возвращаемся к старой переменной} =

tg t

+c =

+c .

1+tg 2t

a2 a2 + x2

Интегралы

вида

где

k ≤ 2 , подстановкой

∫(x

− a)k

x − a = 1 ; dx = −

ax2 + bx + c

dt приводятся к предыдущему случаю.

Пример:

-1

x =

; dx

dt; t

∫ x x2 +1

antigtu

= ∫

= −∫

+ c =

= −ln

t + 1+t2

1+t

1+t2

t2 +1

+ c .

−ln

1 +

6.3.4. Интегриров ние дифференциальных биномов

Выражение

вида xm (a +bxn )p dx ,

где

m,n, p

рациональные дроби,

a,b − const , называется дифференциальным биномом.

Интегр л от дифференциального бинома приводится к интегралу от ра-

циональной функции в трех случаях подстановками Чебышева. В ос-

тальных случаях интеграл не вычисляется через элементарные функции.

Случай 1: p

- целое число.

Скачано

240

Лекции 5 - 6

Используется подстановка

x = ts ,

где s

–

НОК

знаменателей дробей

m и n (НОК - наименьшее общее кратное).

Случай 2:

m +1

- целое число.

Используется подстановка a + bxn = ts , где s – знаменатель дроби

Случай 3:

m +1

+ p - целое число.

Используется подстановка ax−n + b = ts , где s – знаменатель дроби p .

Пример:

m = −1, n = 2, p = − 1 .

∫

= ∫x−1 (1 + x2 )−2 dx ,

m +1

= 0 - целое - случай 2, используется замена

1 + x2

= t2 , x2 = t2

−1, x =

t2 −1,

dx =

2tdt

t2 −1

t dt

t +1

∫

= −∫

= − 2 ln

t −1

+c =

t2 −1 t2 −1 t

t2 −1

1−t2

= ln

−

+c = ln

x2 +1

−1

+c.

x2 +1

antigtu

6.3.5. Метод неопределенных коэффициентов для интегрирования

иррациональн стей

Pn (x)

В общем случае интегралы вида ∫

можно вычислить, ис-

+ bx + c

пользуя следующую формулу:

∫

Pn (x)

dx = Qn−1 (x)

+ bx + c + λ∫

ax2

+ bx + c

ax2 + bx + c

Скачано

где Qn−1 (x) - многочлен степени n-1 с коэффициентами, подлежащими определению. Число λ и неопределенные коэффициенты многочлена Qn−1 (x) находятся дифференцированием вышеприведенной формулы.

Пример:
∫			x2	dx = ( Ax + B) x2 + x +1 + λ∫		dx	.
∫	x	2	+ x +1	dx = ( Ax + B) x2 + x +1 + λ∫	x	2	.
	x		+ x +1		x	+ x +1
Дифференцируем по х

Неопределенный интеграл

241

= A x2 + x +1 +

( Ax + B) (2x +1)

+ λ

x2 + x +1

2 x2 + x +1

x2 + x +

Находим неопределенные коэффициенты.

= A(x

+ x +1)+( Ax

+ B)

antigtu

+λ .

x2 : 2 A =1; x : A + B +

= 0; x0 : A +

+ λ = 0,

A =

, B = −

= −

, λ = −

1 .

x2dx

−

+ x +1 −

∫ x2 + x +1

x −

+ x +1 −

x +

+ x

+ C .

, где k – любое, подстановкой

Интегралы виды

∫(x − a)k

ax2 + bx + c

x − a = 1 , dx = −

приводятся к предыдущему случаю.

Пример:

∫

−1 =

; dx = −

dt =

Скачано

−

+3x

= −

∫

t3dt

= −

∫

t2dt

+ 3

+5t +1 +

= −

−

∫ 5t2 +5t +1

6.3.6. Подст новки Эйлера

В общем случае интегралы вида

∫R(x,

ax2 +bx+c)dx

можно вычис-

лить, используя подстановки Эйлера.

Указ нные подст новки классифицируются по виду коэффициентов a, b, c. Предполагается, что квадратный трехчлен не имеет равных действительных корней, так что орень из него не может быть заменен рациональным выражением.

242

Лекции 5 - 6

Первая подстановка Эйлера: a > 0

Используется замена

ax2 + bx + c = t ±

ax .

Выберем

для

определенности

знак

Возведем

в квадрат и

выразим

x =

t2 − c

. Поскольку x -

рациональная функция от t, то dx и t +

ax есть

b − 2t

также рациональные функции от t.

Пример:

∫

; x2 +1 = x + t; x2 +1 = x2 + 2xt + t2 ,

x2 +1

−t2

x =

−

;

dx =

−

dt = −

dt ,

x2 +1 =

1−t2

1−t2 + 2t2

1+ 2 .

1+t

−∫

= −∫

= −ln

+c =ln

+ c .

1+t2

x2 +1 − x

Избавимся от иррациональности в знаменателе дроби под знаком лога-

рифма, умножив чи литель и знаменательantigtuна выражение

x2 +1 + x , то-

гда: ln

= ln

x2 +

1 + x

= ln (

+1 + x).

− x

(

x2 +1)

− x2

Вторая подстановка Эйлера: c>0

Используется заме а

ax2 + bx + c = xt ± c . Выберем для определенно-

сти знак «+».

Пример:

∫

; 1 + x2 = xt +1, 1+ x2 = x2t2 + 2xt +1; x2 = x2t2 + 2xt; x = xt2 + 2t ,

1 + x2

x =

; dx =

2(1 −t2 )+ 2t 2t

dt =

2 − 2t2 + 4t2

dt =

2(1 + t2 )

dt ,

−t 2

1 −t

2 2

1 −t

)

(

1+ x2 =

t 2t

+1 =

2t2 +1−t2

1+t2

1−t2

∫

= ∫

2 (1+t2 )dt

= 2∫

= ln

t +1

1+ x

(1−t

)

2 (1+t

)

−t

t −1

(1−t2 )

Скачано

Неопределенный интеграл

243

x2 +1 −1

x2 +1 −1+ x

= ln

x2 +1 −1

−1

x2 +1 −1− x

2t antigtu,

−1 =

−1)t =

t2 +1

−1 t =

Третья подстановка Эйлера

В этом случае квадратный трехчлен имеет действительные корни α и β .

Используется замена

ax2 + bx + c = (x −α)t .

Пример:

∫

; x2 −1 = (x −1)(x +1), x2 −1 = (x −1) ,

x2 −1

(x −1)(x +1)= (x −1)2 t2 , (x +1)= (x −1)t2 ,

t2 =

x +1

;t =

x +1

; x +1 = xt2

−t2 ,

x −1

x =

t2 +1

;dx =

2t (t2 −1)−2 (t2 +1)

= −

dt ,

(

)

t2 −1

(

)

−

−1

Скачано

=−2сdt

−4t

(

t2 −1

∫

)

∫ x2 −1

∫t2 −1

∫1−t2

(

)

t2 −1

t +1

x +1

x +1 + x −1

x −1

= ln

t −1

x +1

−1

x +1 − x −

x −1

= ln

x −1+2 x2 −1 + x +1

= ln

(x + x2 −1)

x + x

−1

+c .

x +1− x +1

! На с мом деле во всех возможных случаях достаточны первая и третья подстанов и. Действительно, если квадратный трехчлен имеет действительные корни, то применима третья подстановка. Если действительных корней нет, т.е. дискриминант b2 −4ac <0 , то трехчлен

244		Лекции 5 - 6
.	ru

ax2 + bx + c = 41a (( ax + b )2 −( b2 − 4ac )) при всех значениях x имеет знак a.

Случай a<0 нас не интересует, так как радикал в этом случае вовсе не имеет


Скачано	с	antigtu
Скачано	с	antigtu

вещественных значений, значит проходит первая подстановка для a>0.

В результате изучения материала, изложенного в этих лекциях, студенты должны знать:

таблицу основных интегралов;основные методы интегрирования (непосредственное интегрирование, за-

мена переменной, интегрирование по частям).

Студент должен уметь:

вычислять интегралы от основных типов функций (рациональные дроби, выражения, содержащие тригонометрические функции, иррациональные выражения).

Лекции 7 - 8	.	ru
Лекции 7 - 8
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

antigtu

Развитая в прошлой лекции техника вычисления первообразных находит конкретные геометрические и механические приложения в виде определенного интеграла, вычисление которого через основную формулу интегрального исчисления (формулу Ньютона – Лейбница) сводится к вычислению первообразных.

7.1. Определенный интеграл и его свойства/ Основные определения 7.2. Геометрический смысл определенного интеграла 7.3. Теоремы существования 7.4. Свойства определенного интеграла 7.5. Формула Ньютона-Лейбница

7.6. Замена переменной в определенном интеграле 7.6.1. Интегралы от четных и нечетных функций

7.7. Интегрирование по частям 8.1. Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур 8.1.1. Вычисление площади в прямоугольных координатах 8.1.2. Параметрическое задание линий

	с
8.1.3. Вычисление площадей, фигур, граница которых задана кривыми в
параметрической форме
8.1.4. Полярные координаты на плоскости
8.1.5. Связь полярных координат		декартовыми
8.1.6. Примеры уравнений линий в полярной системе координат
Скачано		ектора в полярной системе координат
8.1.7. Площадь криволинейного

8.2. Вычисление длины дуги кривой 8.2.1. Вычисление длины пл ской кривой в прямоугольных координатах

8.2.2. Вычисление длины пл ской кривой в параметрической форме 8.2.3. Вычисление длины дуги пространственной кривой в параметриче-

ской ф рме 8.2.4. Диффере циал длины дуги кривой

8.2.5. Дли а кривой, заданной в полярных координатах 8.2.6. Площадь поверх ости вращения

8.3. Вычисление объемов тел 8.3.1. Вычисление объемов по заданным площадям поперечных сечений

8.3.2. Вычисление объемов тел вращения

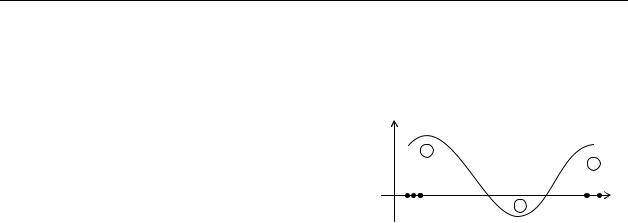
246 Лекции 7 - 8

7.1. Определенный интеграл и его свойства. Основные определения

Пусть на

[a, b]

задана непрерыв-

ная функция f (x). Разобьем [a, b]

на

частей точками

деления:

a = x0 < x1 < x2 < ... < xn = b .

Обозначим: +x1 = x1 − x0 ,

x0ξ1 x1 ...

–

xn−1xn

+x2

= x2 − x1 ,… +xi = xi − xi−1 ….

Рис. 1.1

каждом

из

отрезков

[xi−1 ,xi ]

возьмем по точке ξi

[xi−1 ,xi ].

Составим сумму: Sn

= f (ξ1 )+x1 + f (ξ2 )+x2 +... + f (ξn )+xn = ∑ f (ξi )+xi .

i=1

Геометрически Sn есть алгебраическая сумма площадей прямоугольни-

ков, имеющих основания ∆хi и высоты f (ξi). S

называют интегральной

суммой для

f (x) на [a, b].

зависит от способа разбиения [

, b] на отрезки [xi−1 ,xi ]

и от выбора

точек ξi

внутри [xi−1 ,xi ].

antigtuвоя S .

Каждому разбиению оответ твует

Таким

образом,

получает я

по ледовательность {Sn} .

Обозначим

max+xi

наибольшую

из длин

отрезков

разбиения

и устремим

max+xi → 0 .

Если при любых разбиениях [a, b]

таких, что max+xi → 0 , и при любом

(ξi )+xi стремится к одному пределу S,

выборе точек ξi

Sn = ∑ f

то этот

i=1

предел н зыв ется определенным интегралом от f (x) на [a, b]

и обо-

значается ∫b

f (x)dx . Таким образом, по определению

∫ f (x)dx =

lim

∑ f (ξi )+xi ;

max+xi →0

i=1

н зыв ется нижним пределом интеграла, b – верхним пределом.

Если ∫b

f (x)dx , то

f (x)

называется интегрируемой на [a, b].

Скачано

7.3. Теоремы существования

Определенный интеграл

247

7.2. Геометрический смысл определенного интеграла

	Геометрически определённый интеграл ∫b	f (x)dx представляет собой ал-
	a			ru
гебраическую сумму площадей фигур, ограниченных графиком					функции
	antigtu		.
	antigtu

у =f(х), осью Ох и прямыми х = а и х = b, причем площади, расположенные выше оси Ох, входят со знаком плюс, а площади, расположенные ниже оси Ох, - со знаком минус.

Если f (x)

непрерывна на [a, b], то она интегрируема на [a, b].

Если f (x)

кусочно-непрерывна на [a, b] (имеется конечное число точек

разрыва первого рода), то она интегрируема на [a, b].

Если f (x)

монотонна на [a, b], то она интегрируема на [a, b].

∫b

f (x)dx

В определении

пределы удовлетворяют ограничению

a < b .

Снимем это ограничение.

Е ли

a < b , то

∫ f

(x)dx = −∫ f (x)dx .

Пусть

Скачано

также ∫a

f (x)dx =0 .

Пример:

Вычислить∫b kxdx как предел интегральных сумм.

Решение:

+xi

= b −a

=+x ;

x0 = a;

x1 = x0 ++x;

x2 = x1 ++x = x0 + 2+x.

Пусть ξi = xi−1 (левые концы каждого отрезка)

ξ1 = x0 ; ξ2

= x1 и так далее.

Sn = ∑ f (ξi

)+xi

= ∑kxi −1 b − a = k (b − a)∑xi −1 =

i =1

(b − a)

∑ a

+ (i −1)

248

Лекции 7 - 8

k (b − a)

− a)

k (b − a)

(b − a)

n (n −1)

∑a +

∑(i

−

na +

k (b − a){an2

+ bn2 −

(b − a)n}

antigtu

Для интеграла в левой ча ти

Пусть n → ∞(+x → 0)

, lim S

= k

(

−a2

)

∫

kxdx = k

(

−a2

)

n→∞

7.4. Свойства определенного интеграла

1. Независимость величины интеграла от обозначения переменной интег-

рирования: ∫b

f (x)dx = ∫b

f (t )dt .

f2 интегрируемы на

2. Линейность определенного интеграла. Если

[a,b] и А, В – произвольные числа, то

∫b [Af1

+ Bf2 ]dx = A∫b

f1dx + B∫b

f2dx .

Доказательство:

S =

Af (ξ )+ Bf (ξ ) +x =

Скачано

∑

2 i

i=1

= ∑Af1 (ξi )+xi + ∑Bf2 (ξi )+xi =

i=1

(ξi

)+xi .

= A∑ f1 (ξi )+xi + B∑ f2

i=1

По условию

∑ f1

(ξi )+xi → ∫ f1 (x)dx ,

∑ f2

(ξi )+xi → ∫ f2 (x)dx .

i=1

f1dx + B

f2dx lim

Таким обр зом,

lim

правой части A

∫

ле-

max+xi →0

вой части ∫b [Af1 + Bf2 ]dx = A∫b

f1dx + B∫b

f2dx , что и требовалось доказать.

3. Аддитивность (разбиение промежутка интегрирования на части).

Для любых трех чисел a ,

b ,

c справедливо равенство:

∫b

f (x)dx = ∫c

f (x)dx + ∫b

f (x)dx

при условии, что все три интеграла существуют.

Определенный интеграл

249

Доказательство:

где c - точка деления [a, b].

Пусть a < c < b . Составим ∑

для ∫

∑ соответствует ∫

; ∑ соответствует ∫

, ∑

= ∑

+ ∑ перей-

дем к пределу при max+xi → 0 : ∫ f (x)dx = ∫ f (x)dx + ∫

f (x)dx .

Если a < b < c , то ∫c

= ∫b

+ ∫c

; ∫b

= ∫c

− ∫c

= ∫c

+ ∫b .

Теоремы об оценке определенного интеграла

Сохранение интегралом знака функции. Пусть 1) f (x) интегрируема

на [a, b]; 2)

f (x) ≥ 0

для любых x [

,b], тогда ∫b

f (x)dx ≥ 0 .

Доказательство:

(ξi )+xi

f (x)dx ≥ 0 , что и требовалось

Sn = ∑ f

≥ 0 lim Sn

≥ 0 , то есть

∫

n→∞

i=1

antigtu

доказать.

Интегрирование неравенств.

Пусть 1)

f (x),

g (x)

f (x)≥ g (x)

для любых

интегрируемы на [a, b]; 2)

x [a,b], тогда:

∫b

f (x)dx ≥ ∫b g (x)dx .

Доказательство:

f (x)− g (x)≥ 0 b

f (x)− g (x) dx ≥ 0 .

∫

∫b

f (x)dx − ∫b g (x)dx ≥ 0 ∫b

f (x)dx ≥ ∫b g (x)dx

Теорема

об

оценке.

Пусть

f (x)

интегрируема

на

[a, b];

2) m и M -н именьшее и наибольшее значения функции f (x),

тогда

m(b − a)≤ ∫b

f (x)dx ≤ M (b − a).

Скачано

250

Лекции 7 - 8

Доказательство:

Из условия теоремы m ≤ f (x) ≤ M .

Интегрируем неравенство 1:

antigtu

∫b mdx ≤ ∫b

f (x)dx ≤ ∫b Mdx .

Из линейности ∫b mdx = m∫b dx = m(b − a).

Теорема о среднем. Если

f (x) непрерывна на [a,b], то c [a,b] такая,

что ∫b

f (x)dx = (b − a) f (c).

Доказательство:

∫b

Из

теоремы

об

оценке

m ≤

f (x)dx ≤ M , то есть

(b − a) a

∫b

f (x)dx = µ ,

где m ≤ µ ≤ M .

(b − a) a

f (x)

Так как

непрерывна, то она принимает все промежуточные значе-

ния между m и M. Следовательно, при некотором значении с (c [a,b])

f (c)

= µ , то есть

∫b f

(x)dx = (b − a) f (c).

Скачано

Число f (c)=

(b - a)

∫ f (x)dx

называется средним значением функции

f (x)

на отрезке [a, b].

Пример:

dx .

Оценить интеграл ∫

Решение:

1+ x 4

Имеем 1 ≤ 1 + х4 ≤ 2 при 0 ≤ х ≤ 1,

1 ≤

≤1,

1+ x 4

т.е. m = 1 , М = 1, b − а = 1.

Следовательно, 1

dx ≤ 1.

≤ ∫

0 1+ x 4

Определенный интеграл									251
	Пример:
	Пример:
				1			.	ru
		Определить знак интеграла ∫x3e x dx , не вычисляя его.
		Решение:		−1
		Решение:		1	0	1
				1	0	1
		Разобьём интеграл на два ∫x3 exdx = ∫x3 exdx + ∫x3 exdx =
				−1	−1	0
		={поменяем в первом интеграле пределы}=
		={поменяем в первом интеграле пределы}=
		−1	1
		= − ∫ x3 ехdx + ∫x3 ехdx =
		0	0
		={заменим в первом интеграле х → (−х), тогда:}=
		1	1	1		1
		= − ∫(− x)3 е−х d(−x) + ∫x3 ехdx = − ∫ x3 e−xdx + ∫x3 ехdx =
		0	0	0		0
		1
		= ∫x3 (ex − e−x) dx, на отрезке х [0, 1], х3 ≥ 0, ех − е−х ≥ 0,
		0
			1
		следовательно, ∫x3 (ex − e−x) dx ≥ 0, т.е. знак интеграла - плюс.
			0
Производная интеграла по верхнему пределу (теорема Барроу)
	Рассмотрим некоторый промежуток [				, b],	f (x)- функция, интегрируе-

мая на [a, b], d – фиксированная точка из [a,b], х – любая точка из

[a, b]. Из

интегрируемости f

(

)

на

[

a, b

]

ледует интегрируемость

(

)

на

[

d ,x

]

. Ес-

antigtu

ли верхний предел меняется, то меняет я и значение интеграла ∫x

f (t )dt , т.е.

можно сказать, что на [a, b]

(x): F (x) = ∫ f (t )dt .

задана функция F

Функция F (x)

азывается интегралом с переменным верхним преде-

лом.

′

Если f (x) непрерывна на [a, b], то F′(x) = ∫ f (t )dt

= f (x)

- произ-

водная от интеграла по переменному верхнему пределу равна результату

подстановки значения верхнего предела в

подынтегральную

функцию f (x).

Док з тельство:

F (x ++x)− F (x)

По определению производной F′(x)

= lim

Скачано

+x→0

252

Лекции 7 - 8

x++x

F (x ++x)− F (x)=

∫

f (t )dt − ∫ f (t)dt

{из

свойства аддитивности}=

x++x

= ∫ f (t )dt + ∫ f (t )dt − ∫ f

(t)dt = ∫ f

(t )dt = f (µ)+x , x < µ < x ++x ,

(x ++x)− F (x)

f (µ),

µ → x

lim

= lim

так

как

при

+x → 0 ,

то

+x→0

f (x).

lim f

(µ) = lim f (µ) = f (x) F ′(x) =

+x→0

µ→x

Теорема Коши.

Всякая непрерывная на [a, b] функция

f (x) имеет в

этой области первообразную F (x)= ∫x

f (

или, так как первообразная

определяется с точностью до константы, F (x)= ∫x

f (t )dt + C , C −const .

(x) дифферен-

(Обобщение теоремы Барроу). Если функции ϕ (x)

и ψ

цируемы в точке х [a, b]

и f (t ) непрерывна при ϕ(a)≤ t ≤ψ (b),

то

ψ (x)

′

)

∫

(t)dt = f ψ (x) ψ

′

(x)− f ϕ

(x)

′

(x)

(

)

(

ϕ(x)

antigtu

Пример:

I(х) =

−t

dt, найти I′(х).

∫

Решение:

Учтём ϕ(х) = 0, т.е. ϕ′(х) = 0, ψ(х) = х2.

I′(х) = e −(x2 )2 (х2)′ = 2хe−x4 .

7.5. Формул Ньютона-Лейбница

Пусть

f (x)

непрерывна на [a, b], тогда

∫b

f (x)dx = F (b)− F (a)= F (x)

ba .

До азательство:

По теореме Коши из условия непрерывности f (x)

следует существова-

ние F (x)= ∫x

f (t )dt + C .

Скачано

Определенный интеграл								253
Положим, x = a		F (a)= ∫a	f (t )dt + C ,		то	есть C = F (a).	Положим,
		a
x = b F (b)= ∫b	f (t)dt + F (a) ∫b			f (t )dt = ∫b		f (x)dx = F (b)− F (a), что и
a			a		a	.	ru
требовалось.						.	ru

Таким образом, для вычисления определенного интеграла от непрерывной функции f (x) нужно:

1) не обращая внимания на пределы интегрирования найти первообразную F (x) для подынтегральной функции (по правилам вычисления

неопределенного интеграла); 2) вычислить F (b)− F (a).

Пример:

∫b kxdx = k ∫b xdx = k

= k (b2

− a2 ).

π∫sin xdx = −cos x

π0 = −cosπ + cos 0 = 2 .

Пример:

antigtu

Вычислить ∫

x ln x

Решение:

e2 d(ln x)

∫

= ln

ln x

= ln(ln e ) − ln(ln e) = ln 2 ≈ 0,69.

x ln x

ln x

Пример:

Вычислить

∫4

cos

Решение:

π 4

= tgx

π∫

cos2 x

= tg

− tg 6

= 1 −

7.6. З мена переменной в определенном интеграле

Т Пусть 1) f (x)

непрерывна на [a, b]; 2) x = g (t )

- непрерывно диффе-

ренцируема на

α, β

]

(

a,b

]

- область значений

)

при изменении

[

(

Скачано

Левая часть

∫b

f (x)dx = F (b)− F (a).

254

Лекции 7 - 8

t [α,β]); 3)

a = g (α ),

b = g (β ), тогда ∫b

(g (t))g′(t )dt - форму-

f (x)dx = ∫ f

ла замены переменной под знаком определенного интеграла

Доказательство:

antigtu

Здесь F (x) = F (g (t )).

Ft′ = Fx′ xt′ = F ′(g (t )) g′(t );

F ′(g (t ))= F ′(x) = f (x) = f ( (t )).

Таким образом, Ft '

= f (g (t )) g' (t ),

следовательно,

F (g (t )) является перво-

образной для функции

f (g (t )) g'

(t )

на [α,β].

(

))

(

)

(

))

(

))

Правая часть

∫

g '

−

, то есть

t dt =

(

))

(

)

(

)

(

)

∫

g '

= F

− F

. Левая часть равна правой части, что и тре-

t dt

бовалось доказать.

Пример:

x = r sin t,

0=r sinα, α = 0

Скачано

∫ r2 − x2 dx =

r=r sin β,

dx = r cos tdt,

= π∫/ 2

r2 −r2 sin2 tr cos tdt = π∫/ 2 r2 cos2 tdt =

π∫/ 2 (1+ cos 2t )dt =

πr2

sin 2t

Пример:

∫1 x x2 +

= x =

dx=-

,1=

,α =1,2

∫1

=ln (t+ t2 +1)

= −∫2

tdt

11 =

ln (1+

2 )-ln

5 .

2 1+t

1+t

Определенный интеграл

7.6.1. Интегралы от четных и нечетных функций на [−a,a]

1) f (x)

- четная ( f (−x) = f (x)).

∫a

f (x)dx = ∫0

f (x)dx + ∫a

f (x)dx .

−a

x = −t, dx = −dt

∫ f (x)dx =

−a = −α, a = α

−a

0 = −β,

β = 0

= −∫0

f (−t )dt = ∫a

f (t )dt = ∫a

f (x)dx ,

∫a

f (x)dx = 2∫a

f (x)dx .

−a

f (x) - нечетная функция

( f (−x) = − f (x)).

∫a

f (x)dx = ∫0

f (x)dx + ∫a

f (x)dx .

antigtu

−a

x = −t, dx = −dt

f (x)dx =

∫

−a = −α, a = α

−a

0 = −β,

β = 0

= −∫0

f (−t )dt = ∫0

f (t )dt = −∫a

f (x)dx ,

∫a

f (x)dx =0 .

−a

7.7. Интегриров ние по частям

Пусть u (x)

и v (x)

имеют на

[a, b] непрерывные производные,

b u (x)v′

(x)dx = u

(x)v (x)

− b u′(x)v (x)dx .

∫

Или: т

v '(x)dx = dv , u '(x)dx = du , то ∫b udv = uv

ba − ∫b vdu .

Скачано

255

тогда

256

Лекции 7 - 8

Доказательство:

(uv)' = uv '+ vu ' , ∫b [uv '+ vu ']dx = ∫b (uv)' dx , ∫b uv 'dx + ∫b vu 'dx = v

ba ,

∫b udv = uv

ba − ∫b vdu , что и требовалось доказать.

Пример:

u = arcctgx,

dv = dx

∫arcctgxdx =

du = −

v = x

1+ x

= xarcctgx

+ 2 ln (x

+1)

= 4

+ 2 ln2.

Пример:

Вычислить ∫xe−x dx .

∫xe−x dx ={

u = x, dv = e-xdx, du = dx, v = -e-x} =

1 +

1 =

e −2

= − xe −x

∫e−x dx = -е-1 −e −x

antigtu

8.1. Геометрические прил женияс

определенного интеграла.

Вычисление пл щадей плоских фигур

8.1.1. Вычисле ие площади в прямоугольных координатах

1) f (x)≥ 0 , S = ∫b

f (x)dx .

2) f (x)≤ 0 , S = −∫b

f (x)dx .

Скачано

Определенный интеграл

3) f

(x) ≥ f

(x), S = b f

(x)− f

(x) dx .

∫

antigtu

1)* f (y) ≥ 0 , S = ∫d

f (y)dy .

2)* и 3)* аналогичны 2) и 3).

Пример:

Вычислить площадь фигуры, ограниченной пара-

болой

у = х2, прямыми

х = -1 и х = 2 и осью абс-

цисс .

Решение:

y = x2 .

Скачано

Используем формулу 3.1 S = ∫2

x2dx =

= 3.

Пример:

−1

Вычислить площадь сегмента, отсекаемого прямой у = -х

от параболы у = 2х − х2.

Реше ие:

y = −x .

Преобр зуем ур внение параболы у = 2х − х2 = − (х2 − 2х + 1) + 1, (у −

= − (х − 1) 2.

Находим абсциссы точек пересечения (А и В), имеем:

y = 2x − x2 , x1 = 0,

= 3.

y = −x, x2

S = ∫3 (2x − x2 )−(−x) dx = ∫3 (3x-x2 ) dx =

3 x2 − 1 x3

3 =

9 .

257

1) =

8.1.2. Параметрическое задание линий

258

Лекции 7 - 8

Пример:

Вычислить площадь эллипса

=1.

y = ±b 1−

Sэл = 4∫b 1−

dx = x = a sin t,

= 0, β =

= 4ab∫2 cos2 tdt = [2abt + absin 2t]

= πab , Sэл =πab.

8.1.3. Вычисление площадей фигур, границаantigtuкоторых задана

Параметрические уравнения линий задаются в виде зависимости координат x и y от некоторого параметра t: x = x(t), y = y(t) . При изменении пара-

метра t текущая точка M(x, y) описывает некоторую кривую на плоскости. Исключением параметра уравнение линии приводится к уравнению в декартовых координатах и, наоборот, линия, заданная в декартовых координатах,

может быть приведена к виду кривой, заданной параметрическими уравне-
ниями.		с
ниями.
кривыми в параметриче кой форме
Скачано
Пусть кривая задана параметрическими уравнениями:
x = x (t),		(	)	, b = x	(	β	)	.
		(	)		(		)
		α ≤ t ≤ β , a = x α
y = y (t),

b	b				β
S = ∫ f (x)dx = ∫ ydx ={x = x (t), dx=x′			(t )dt}= ∫ y (t )x ' (t)dt ;
a	a				α

S = ∫y (t )x '(t )dt .

Пример:

Вычислить площадь эллипса.

Уравнения эллипса в параметрической форме имеют вид:

x = a cos t , 0 ≤ t ≤ 2π .

y = b sin t

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

Соседние файлы в папке Математика

#
25.03.20159.85 Mб40kurs_vysshey_matematiki.pdf
#
25.03.201519.71 Кб43БАЗА для экзамена.docx
#
25.03.201523.96 Кб47КР для заочников1.docx