
- •49. Біртекті толқын теңдеуі үшін Коши есебі. Дюамель қағидасы.
- •50. Толқын теңдеуге қойылған аралас шекаралық есепті Фурье әдісімен шешу.
- •52. Жылуөткізгіштік теңдеу үшін экстремум қағидасы және оның қолданылулары
- •53. Біртекті және біртекті емес жылуөткізгіштік теңдеулерге қойылған шекаралық есепті Фурье әдісімен шешу.
- •54. Гармоникалық функциялардың қасиеттері.
- •55. Лаплас теңдеуі үшін шеттік есептің қойылуы және шешімдердің жалғыздығы.
- •56. Шар және шеңбер үшін Пуассон формулалары.
- •57. Лаплас теңдеуі үшін Грин функция әдісі.
55. Лаплас теңдеуі үшін шеттік есептің қойылуы және шешімдердің жалғыздығы.
1-теорема.
Дирихленің ішкі есебінің 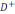 :
:
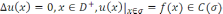 (1)
(1)
шешімі жалғыз.
Дәлелдеу.
Керіжориық
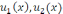 -есептің
екі шешімі болсын, онда
-есептің
екі шешімі болсын, онда 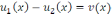 -
айырмасы үшін (1) есеп
-
айырмасы үшін (1) есеп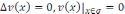 түрінде қойылады; ал бұл біртекті есеп
максимум қағидасы бойынша
түрінде қойылады; ал бұл біртекті есеп
максимум қағидасы бойынша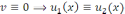 .
.
2-теорема. Дирихленің сыртқы есебінің :
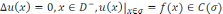 (2)
(2)
шешімі жалғыз.
Дәлелдеу.
x=0
нүкте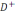 аймақ ішінде жатсын. Инверсиялық
түрлендіру бойынша
аймақ ішінде жатсын. Инверсиялық
түрлендіру бойынша
x=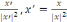
алмастыру
нәтижесінде
шекарасы
 болған шексіз сыртқы
болған шексіз сыртқы 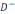 аймақты шекарасы
аймақты шекарасы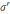 болған
болған
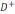 аймаққа келтіріледі де сыртқы (2) есеп
Кельвин түрлендіруі бойынша
аймаққа келтіріледі де сыртқы (2) есеп
Кельвин түрлендіруі бойынша
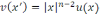
түрге
келтіріп
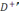 аймақтағы
аймақтағы 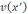 функция үшін Дирихленің мынандай ішкі
есебіне келеміз:
функция үшін Дирихленің мынандай ішкі
есебіне келеміз:
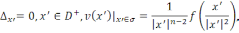
ал бұл есептің 1-теорема бойынша жалғыз шешімі бар.
56. Шар және шеңбер үшін Пуассон формулалары.
Шеңбер үшін қайнар функциясы сфера үшін қайнар функциясы сияқты алынады. Бұл жағдайда оны мына түрде іздейміз:
G=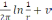
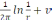 (1)
(1)
(тихонов 347бет)
G функциясын табамыз:
G(P,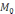
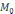 )=
)=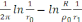
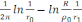 (2)
(2)
Мұндағы

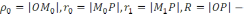 шеңбердің
радиусы
шеңбердің
радиусы


R. R
осылайша анықталған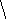
гармоникалық функция
мына шекарада нөлге айналады:
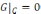
Бірінші
шекаралық есептің шешімін табу үшін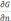
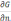 мәнін С аймағында (окружность) есептеу
керек. есептеу сферадағыдай жүреді және
келесіні береді:
мәнін С аймағында (окружность) есептеу
керек. есептеу сферадағыдай жүреді және
келесіні береді:
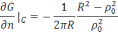
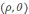
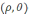 -
шеңберде жатқан Р нүктесінің полярлы
координатасы,
ал
(
-
шеңберде жатқан Р нүктесінің полярлы
координатасы,
ал
(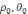
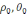 )-
)-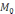
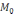 нүктесінің координатасы, онда
нүктесінің координатасы, онда
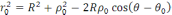
Формулаға қойсақ:
u(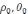
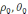 )=
)=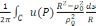
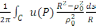
бұл
өрнекті
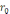
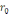 үшін
және
келесіні
ескерсек
үшін
және
келесіні
ескерсек
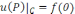
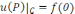 және
ds=Rd
және
ds=Rd

u(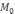
 )
функциясы үшін келесі өрнекке келеміз:
)
функциясы үшін келесі өрнекке келеміз:
u(
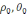 )=
)=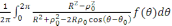
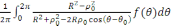 (3)
(3)
ал мұны шеңбер үшін Пуассон интегралы деп атаймыз. Бұл тура ішкі есептің шешімін береді.
Шар аймақта Дирихле есебін Грин функциясы әдісімен шешу. Шардың центрі координата жүйесінің бас нүктесінде жатсын, ал
радиусы
R болсын. Онда сфераның бетінің теңдеуі
|x|=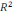
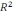 .
Шардың ішкі х нүктесіне сәйкес, сфераның
бетіне симметриялы Ох радиус векторының
бойынан, олардың радиус вектторлары
|x||x’|=
.
Шардың ішкі х нүктесіне сәйкес, сфераның
бетіне симметриялы Ох радиус векторының
бойынан, олардың радиус вектторлары
|x||x’|=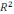
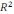 болатындай x’ нүктені таңдаймыз.
Белгілеулер r=|x-
болатындай x’ нүктені таңдаймыз.
Белгілеулер r=|x-
 |,
|,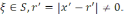
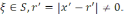 үшбұрыштар
үшбұрыштар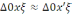
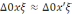 ,
себебі
,
себебі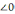
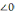 ортақ, сәйкес қабырғалары
ортақ, сәйкес қабырғалары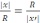
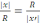 пропорционал болғандықтан, екі үшбұрыштың
ұқсастығынан
пропорционал болғандықтан, екі үшбұрыштың
ұқсастығынан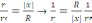
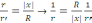 аламыз.
аламыз.
Екі жағын дәрежелесек, онда
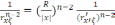
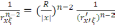 (1)
(1)
Шар аймақ үшін бірінші шекаралық есептің Грин функциясы
Q(x,
 )=
)=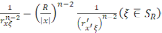
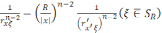 (2)
(2)
екеніне
көз жеткізу қиын емес. Функция
g(x,
 )=
)=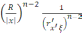
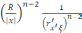 аргумент
xжәне
аргумент
xжәне

 бойынша
бойынша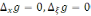
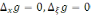 гармоникалық
функция.
Нүкте
гармоникалық
функция.
Нүкте 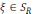
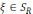 жатса,
онда (2) теңдіктен
жатса,
онда (2) теңдіктен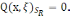
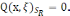 Сонымен
Грин функциясының 1-2 шарттары орындалады.
Сондықтан Лаплас теңдеуі үшін Дирихле
есебінің шешімі келесі теңдктен
Сонымен
Грин функциясының 1-2 шарттары орындалады.
Сондықтан Лаплас теңдеуі үшін Дирихле
есебінің шешімі келесі теңдктен
U(x)=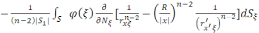
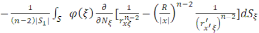

Формуламен анықталады.
Сфераға
жүргізілген нормаль 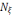
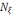
радиуысына бағыттас болатынын


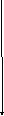



ескеріп, нормальді туынды
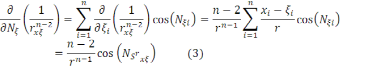
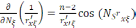
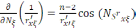 (4)
теңдіктерді алуға болады. Үшбұрыштар
(4)
теңдіктерді алуға болады. Үшбұрыштар
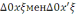
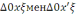 косинустар теоремасы бойынша
косинустар теоремасы бойынша
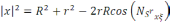
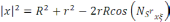 (5)
(5)
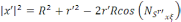
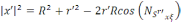 (6)
(6)
Формулалар

 және
(5)-(6) пайдаланып күрделі емес түрлендіруден
кейін
және
(5)-(6) пайдаланып күрделі емес түрлендіруден
кейін
U(x)=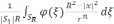
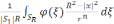 (7)
(7)
Пуассон формуласын аламыз.
(7) теңдік оң жағында интеграл Пуассон интегралы, өзегі
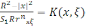
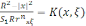 пуассон
өзегі деп аталады.
пуассон
өзегі деп аталады.
57. Лаплас теңдеуі үшін Грин функция әдісі.
Шекарасы
үзік жатық S болатын Ω аймақта анықталған
функциялар
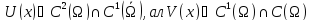 .
.
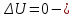 Лаплас
теңдеуі
Лаплас
теңдеуі
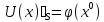 шартын
қанағаттандырады.
шартын
қанағаттандырады.
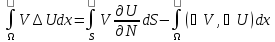 (1)
(1)
(1)-формуласы Лаплас операторы үшін Гриннің бірінші формуласы деп аталады.
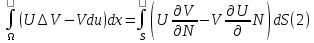
(2)-Лаплас операторы үшін Гриннің 2-формуласы.
Грин
функцияларының анықтамасын беру үшін
алдымен
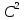 класс
функцияларының интегралдық өрнегі
класс
функцияларының интегралдық өрнегі
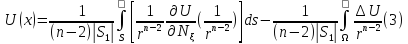
(2)-формуладағы
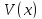 функциясының
орнына екі аргументті
функциясының
орнына екі аргументті
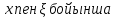 гармоникалық
гармоникалық
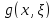 функциясын
қойып, теңдікті
функциясын
қойып, теңдікті
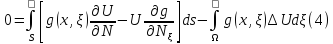
түрінде
жазып екі жағын
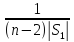 ге
көбейтіп (3)
теңдікке
қоссақ онда
ге
көбейтіп (3)
теңдікке
қоссақ онда
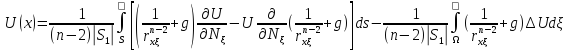
Формуласын аламыз
Анықтама.
Екі аргументті
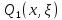 Лаплас теңдеуіне қойылған бірінінші
шекаралық есебінің Грин функциясы
дейді,егер
Лаплас теңдеуіне қойылған бірінінші
шекаралық есебінің Грин функциясы
дейді,егер
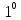 .Ω
аймақта функция
.Ω
аймақта функция
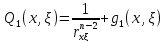
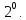 Ω
аймақтың шекарасында
Ω
аймақтың шекарасында
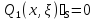 шарттар
орындалса.
шарттар
орындалса.
Грин
функциясы
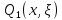 нің қасиеттері
нің қасиеттері
Ω аймақта Грин функциясы
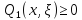 .
.Грин функциясы
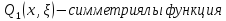 ,
,
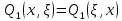 .
.
