7.4. Прямая в декартовой прямоугольной системе координат

7.4.1. Нормальный вектор прямой.

Прямаязадана в системе

Опр. Нормальным вектором прямой называется

любой ненулевой вектор , перпендикулярный

направляющему вектору.

В аффинной системе координат, в частности в дпск, общее уравнение прямой направляющий вектор.

Возьмем вектор как видно,

нормальный вектор. Отсюда ясен геометрический смысл коэффициентов если прямая задана в дпск уравнением

Пусть прямая проходит через точкутогдаВычитая из уравнения прямой, получим:

(11)

Это уравнение прямой с нормальным вектором и проходящей через точку

7.4.2. Уравнение прямой с угловым коэффициентом

где или

7.4.3. Расстояние от точки до прямой

Пусть в дпск заданы прямая и точка

Найдем расстояниеот точки до прямой.

Вычислим скалярное произведение

(12)

Задача. Найдите расстояние от точки до прямой

Задача. Найдите расстояние между прямыми:

7.4.4. Угол между прямыми.

Опр. Углом между двумя прямыми называется угол между их направляющими векторами.

Из определения следует, что углом между двумя прямыми является один из 4-х углов при их пересечении.

Опр. Угол называется направленным, если указан порядок его сторон.

Пусть

или (13)

Условие параллельности : или

Условие перпендикулярности: .

Задача. Найдите проекцию точки на прямую

7.4.5. Решение задач.

№1. Составьте уравнения прямых, параллельных прямой и отстоящих от точкина расстояние

№2. Найдите точку симметричную точкеотносительно прямой

№3. Точка является вершиной правильного треугольника, её противоположная сторона:Составьте уравнения двух других сторон.

№4. Составьте уравнение биссектрисы того угла между прямыми внутри которого лежит точка

№5. Центр симметрии квадрата есть точка уравнение одной стороныСоставьте уравнения других сторон.

№6. Докажите, что ортоцентр, центр тяжести и центр описанной окружности треугольника лежат на одной прямой –прямой Эйлера.

№7. Составьте уравнение биссектрисы острого угла между прямыми

№8. Составьте уравнения сторон треугольника, зная одну его вершину

уравнения биссектрисы и медианыпроведенными из различных вершин.

№9. Определите, лежит ли точка внутри или вне треугольника со сторонами

Отв.Вне.

§8. Формулы преобразования координат

8.1. Рассмотрим на плоскости две аффинные системы координат:

(старая и новая системы координат).

Пусть точкаи

Задача преобразования координат состоит в

следующем: выразить старые координаты

точки через новые

Зададим систему относительно

(1)

По правилу треугольника получим: или(используем (1))

(2)

Формулы (2) называются формулами преобразования координат.

Заметим, что матрица перехода от базисак базисув точности совпадает с матрицей из коэффициентов при

в формулах (2). Определитель этой матрицы поэтому система (2) разрешима относительно

Интересны два частных случая.

(А) Перенос начала.

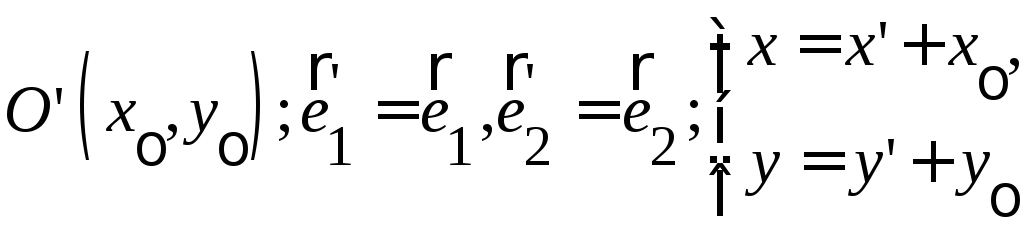
(В) Замена координатных векторов.

Пример. Написать формулы преобразования координат в аффинной системе, если

∆ ▲

8.2. Рассмотрим преобразование прямоугольных координат. Дпск есть частный случай аффинной системы, поэтому можно использовать формулы (2). На коэффициенты матрицы перехода С накладываются определенные условия.

Возможны два случая.

С) Системы ориентированы одинаково (обе правые).

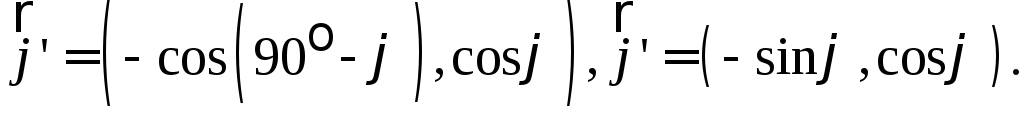
Формулы (2) запишутся так:

D) Системы ориентированы противоположно.

Формулы (2) запишутся так:

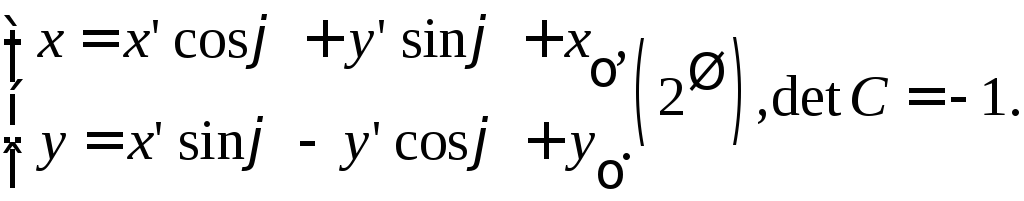
Объединим Формулы

. (3)

(«+» для одинаково ориентированных систем).

Задача. Определите координаты новых векторов и нового начала, если формулы преобразования имеют вид:

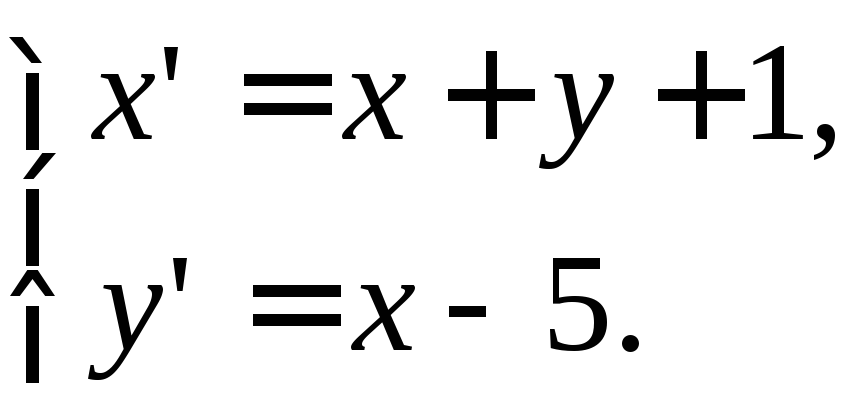отв.

Задача. Напишите формулы преобразования прямоугольных декартовых координат, если и системыодинаково ориентированы.

Отв.