§8. Смешанное произведение векторов.

Опр. Смешанным произведением векторов называется скалярное произведение векторана вектор, то есть число

.

Свойства смешанного произведения.

1. Если векторы ,изаданы своими координатами в декартовой прямоугольной системе координат, то смешанное произведение их вычисляется по формуле:

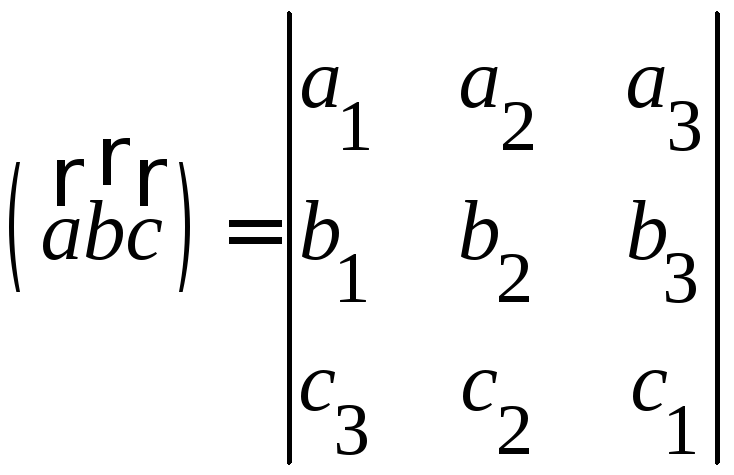
∆ Так как =

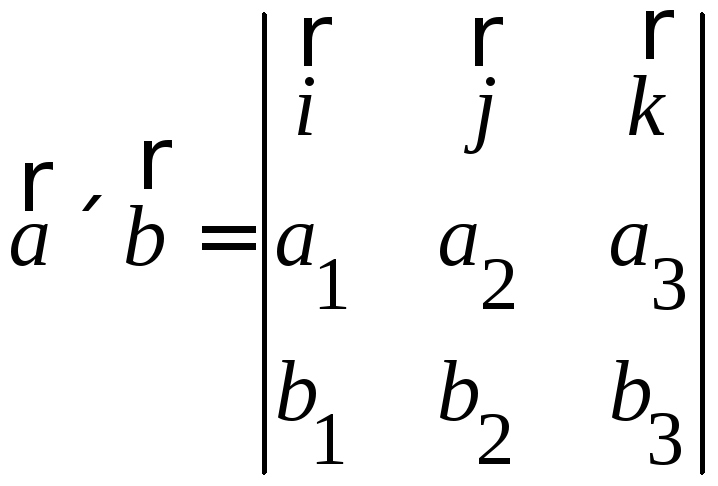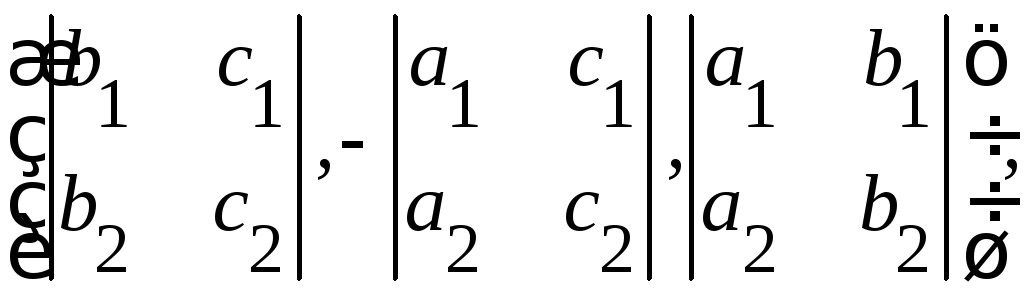
то =

=

▲

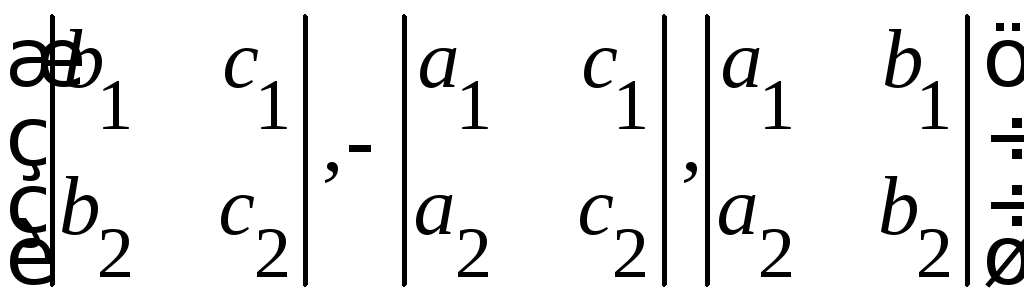
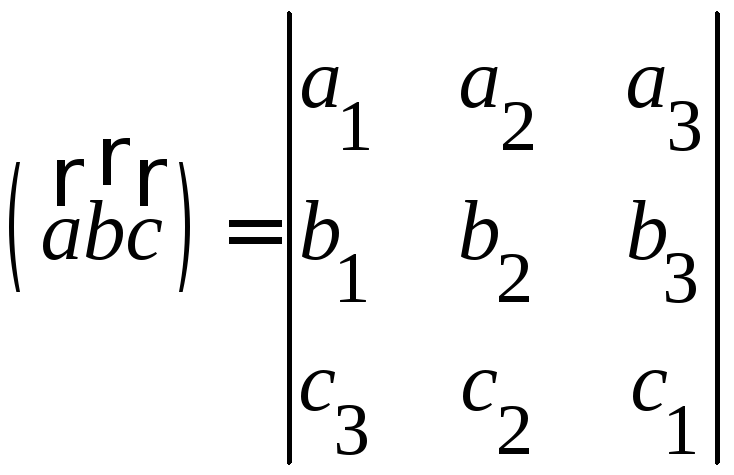
2. Смешанное произведение есть число положительное, если тройка перемножаемых векторов правая, и отрицательное, если – левая.

3. При круговой перестановке сомножителей смешанное произведение не меняется: .

4. От перестановке двух сомножителей смешанное произведение меняет знак: .

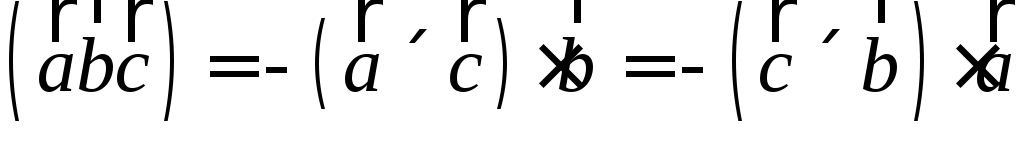5. Скалярное и векторное умножения можно поменять местами: .

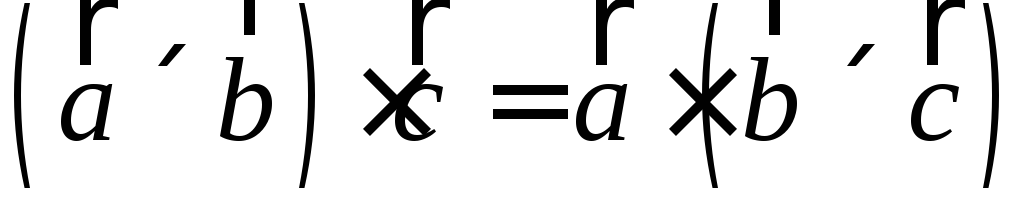6. Числовой множитель можно выносить за знак смешанного произведения:

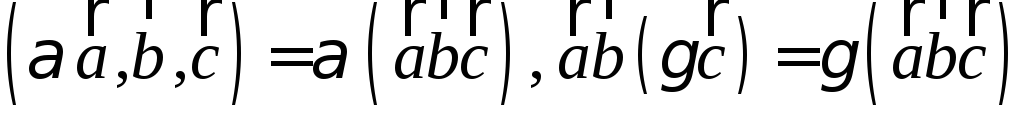
7. Справедлив распределительный закон: .

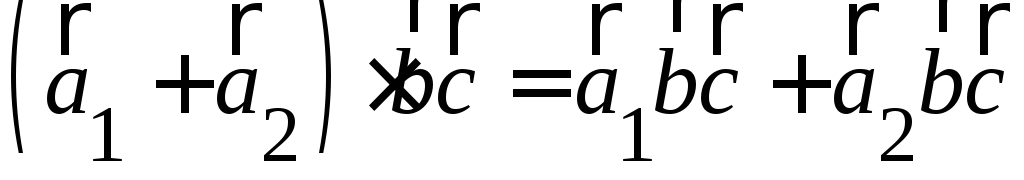8. Геометрический смысл смешанного произведения: в дпск модуль смешанного произведения равен объему параллелепипеда, построенного на перемножаемых векторах:

∆ Пусть некомпланарные векторы ,изаданы в ортонормированном базисе. Перемножаяполучим вектор, модуль которого равен площади параллелограмма,

п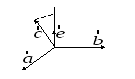остроенного на векторахОбозначим

единичный вектор того же направления

Тогда гдеплощадь

параллелограмма. Умножим этот вектор

скалярно на

Но есть длина высоты параллелепипеда, взятая со знаком «+», если векторрасположен в том же полупространстве относительно плоскостичто и вектори со знаком «-« в противном случае. Таким образом:

Если вектор в том же полупространстве, что ито есть тройкаправая, то имеем знак «+». ▲

Объем пирамиды .

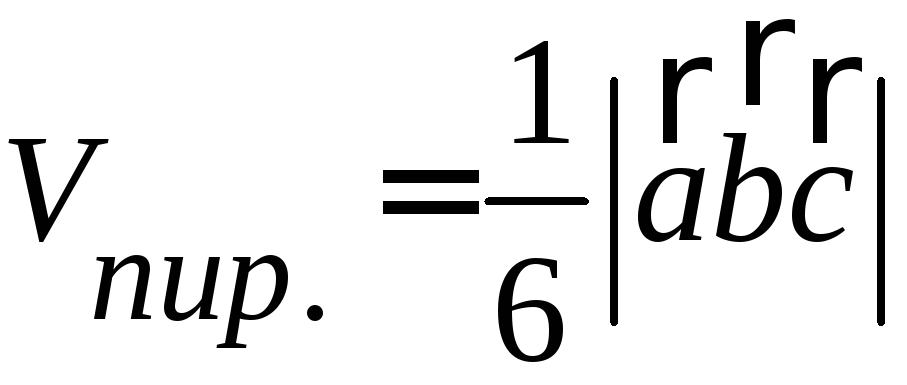2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно 0.

Пример. Найдите объем тетраэдра с вершинами

∆

▲

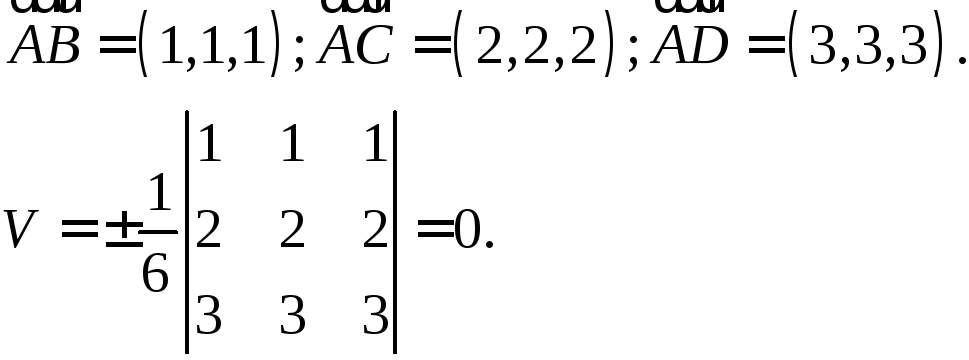
Раздел 2. Метод координат на плоскости

§1. Аффинная система координат

Базис на плоскости образует любая пара неколлинеарных векторов

. Отложим эти векторы от определенной точки О.

Т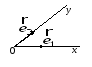ройканазываетсяаффинной системой

координат на плоскости (или обобщенной декартовой

системой координат), или аффинным репером.

Точка О – начало координат, координатные векторы, прямая вектораось абсцисс, прямая вектораось ординат.

Пусть точка на плоскости,её радиус-вектор.

Опр. Координатами точки называются координаты её радиуса-вектора

в базисе

Итак, каждой точке на плоскости соответствует пара действительных чиселОбратно: каждой упорядоченной паре чисел(декартов квадрат множества действительных чисел) соответствует определенная точка на плоскости с координатами

Таким образом, после введения аффинной системы координат на плоскости устанавливается взаимно однозначное соответствие между точками плоскости и парами чисел из

Пример. Постройте точку и векторв данной системе координат.

Задача. В аффинной системе координат даны две точки Найдите координаты вектора

∆

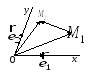
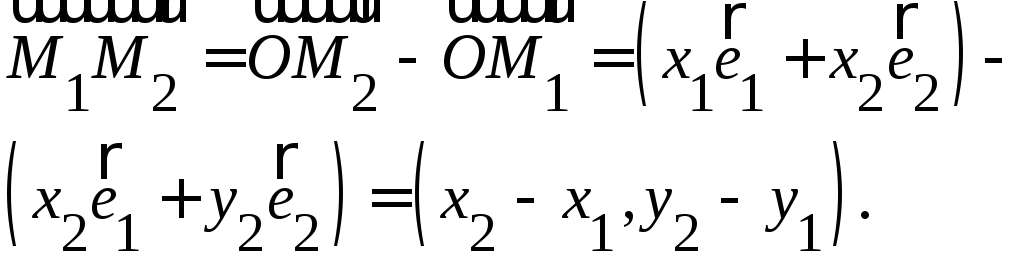
Вывод. Координаты вектора равны разности соответствующих координат конца и начала. ▲