§5. Поверхности 2-го порядка

5.1. Понятие поверхности 2-го порядка

Уравнением поверхности в некоторой системе координат в пространстве называется уравнение

, (23)

которому удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты посторонних точек.

Примеры.

Все поверхности делятся на 2 класса: алгебраические и неалгебраические (траснсцендентные). Алгебраические задаются уравнением (23), если многочлен от 3-х переменных. Степень этого многочлена называетсяпорядком алгебраической поверхности. Свойство поверхности быть алгебраической и её порядок не зависят от выбора аффинной системы координат. Примерами алгебраических поверхностей являются плоскость, сфера. Пример неалгебраической поверхности: цилиндр

Опр. Поверхностью 2-го порядка называется множество точек пространства, координаты которых в некоторой аффинной системе координат удовлетворяют уравнению:

(24)

Здесь действительные числа.

5.2. Цилиндрические поверхности.

Зададим в пространстве некоторую линию

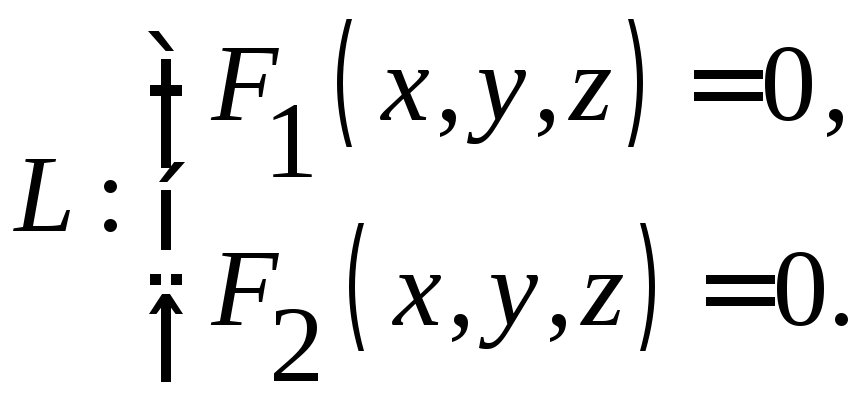(25)

Опр. Поверхность, образованная прямыми пространства, пересекающими некоторую линию и параллельными одной и той же прямой,

пространства, называется цилиндрической поверхностью с направляющей и образующими, параллельными

Пусть в дпск задана направляющая цилиндрической поверхности:

и направляющий вектор образующих Образующие цилиндрической поверхности параллельны оси

Составим уравнение цилиндрической поверхности. Пусть её произвольная точка, прямаяеё образующая, причемТогда выполняется равенствоИ это справедливо для любой точки данной цилиндрической поверхности. Значит, уравнение этой поверхности

Аналогично получаются уравнения цилиндрических поверхностей с образующими, параллельными осям и

Вид цилиндрической поверхности определяется типом направляющей кривой.

Рассмотрим канонические уравнения цилиндрических поверхностей.

1) 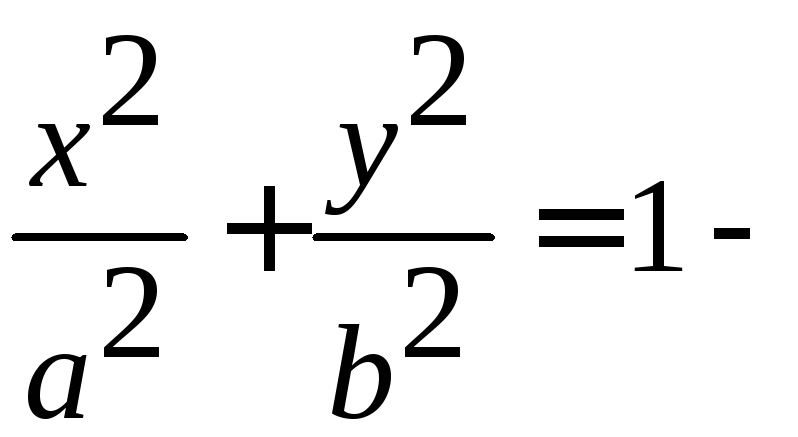эллиптический цилиндр;

]2) гиперболический цилиндр;

3) параболический цилиндр;

4) цилиндр, распавшийся на пару пересекающихся по осиплоскостей;

5) пара мнимых пересекающихся по действительной осиплоскостей;

6) пара параллельных плоскостей;

7) две совпавшие плоскости;

8) мнимый эллиптический цилиндр.

5.3. Конические поверхности

Зададим в пространстве линию

и точку

Опр. Поверхность, образованная прямыми, проходящими через одну точку и пересекающими направляющую линиюназываетсяконической.

вершина конуса

Получим уравнение конической поверхности в дпск с вершиной и направляющей

Пусть произвольная точка конической поверхности, прямая

пересекает напрвляющую в точке Векторыиколлинеарны:

Подставим координаты точки в уравнение направляющей:

(26)

5.4. Эллипсоид

Опр. Поверхность, определяемая в дпск уравнением:

(27)

называет эллипсоидом.

Из уравнения следует, что поверхность симметрична относительно координатных плоскостей, начало координат – её центр симметрии.

Исследуем эту поверхность методом сечений.

1) это эллипс с осями

2) это эллипс с полуосями

3) Если то полуоси уменьшаются и уменьшаются эллипсы в сечениях;

4) При плоскостьповерхность не пересекает.

Аналогично проводится исследование с помощью плоскостей и

параллельных и

Эллипсоид есть овальная поверхность с тремя плоскостями симметрии; полуоси эллипсоида. Если, то эллипсоид трехосный. Эллипсоид – ограниченная поверхность, заключенная в параллелепипеде

Если то в сечениях плоскостямиполучаются окружности.

Этот эллипсоид получается вращением эллипса вокруг оси

мнимый эллипсоид. При имеем сферу.