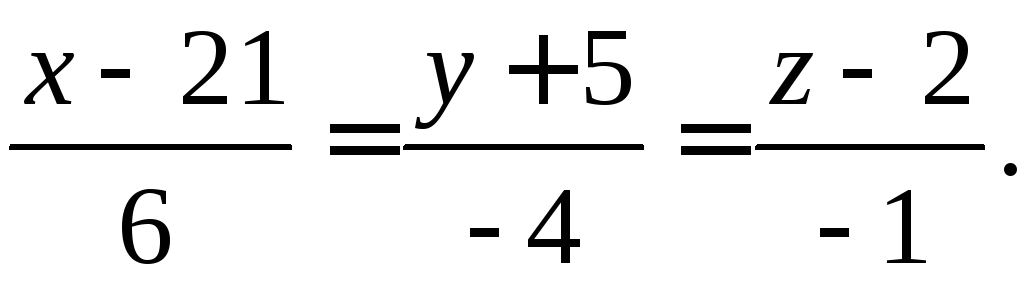§2. Взаимное расположение двух плоскостей
В аффинной системе координат заданы две плоскости
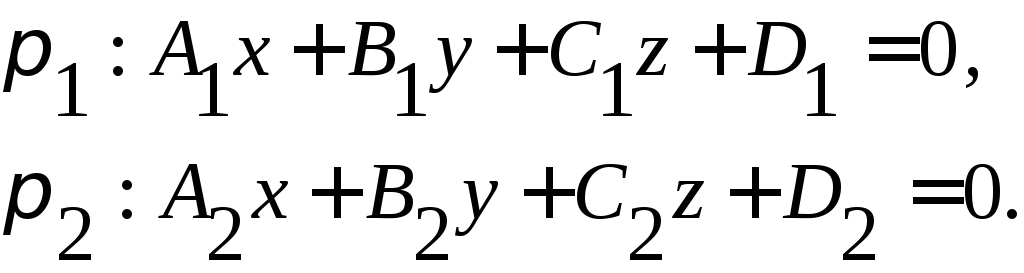(7)
Две плоскости могут совпадать, пересекаться, быть параллельными. Исследуем систему (7). Запишем основную и расширенную матрицы систем и их ранги:
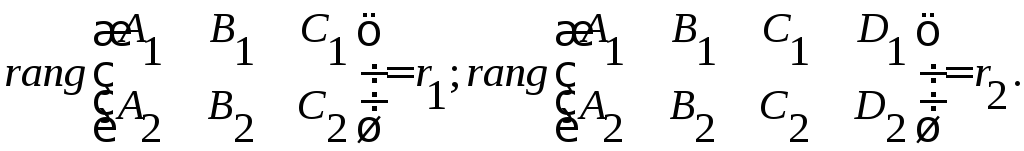
Возможны случаи:
1)
Система
уравнений совместна,
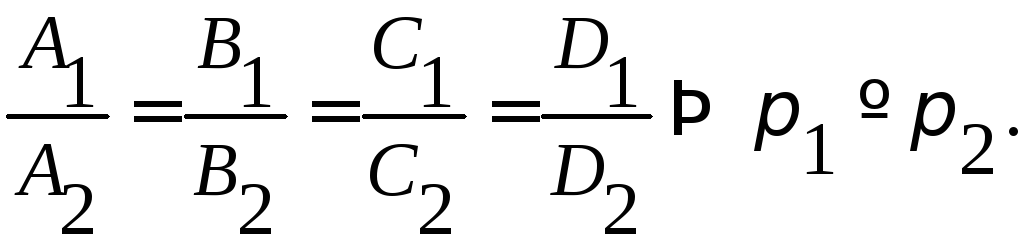
2)
система несовместна,
(8)
3)
система совместна,
Если плоскости имеют общую точку, то они пересекаются по прямой.
Задача.
Через точку
провести плоскость, параллельную
плоскости
§3.Плоскость в дпск. Основные задачи.
Угол между плоскостями.
Пусть в дпск заданы две плоскости:
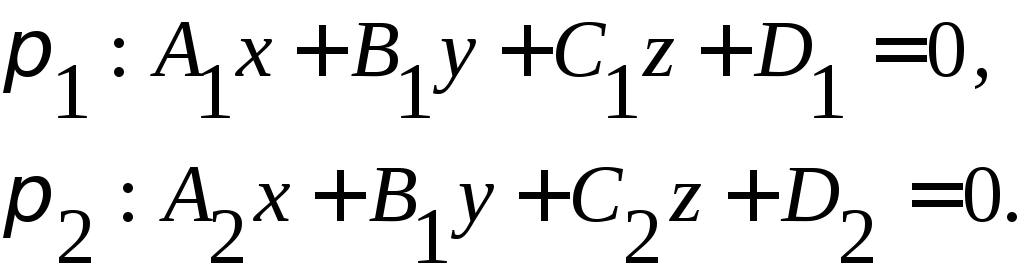
За
угол между плоскостями принимается
любой из двугранных углов, образованных
ими. Он, очевидно, равен углу между их
нормальными векторами:
и
Следовательно, угол между плоскостями
определяется по формуле:
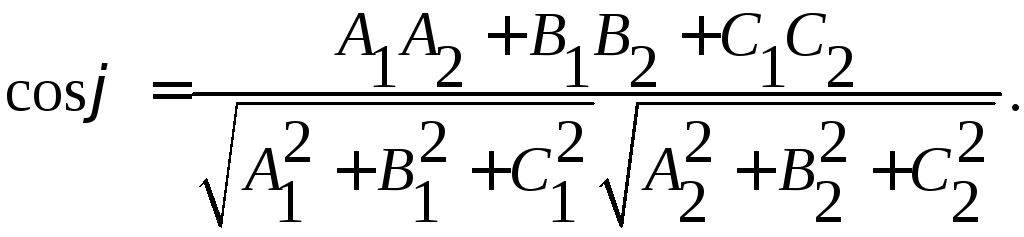(9)
Условие
параллельности
плоскостей
и
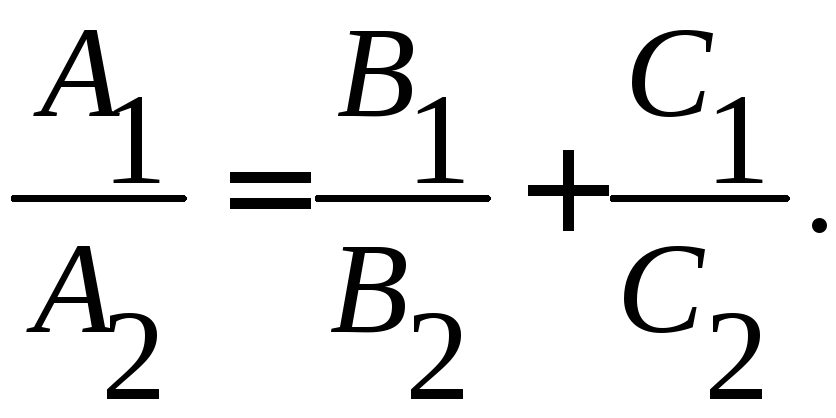(10)
Условие
перпендикулярности
плоскостей
и
(11)
Задача.
Через точку
провести плоскость, параллельную
плоскости
3.2.Расстояние от точки до плоскости.
Пусть
в дпск заданы плоскость
и
точка
Найдем расстояние
от точки до плоскости. Пусть
основание
перпендикуляра, опущенного из точки
на плоскость.
Н
ормальный
вектор
плоскости и
вектор
коллинеарны. Найдем их
скалярное произведение:
Вычислим левую часть этого равенства, учитывая, что
.
Получим:
Раскрывая
скобки в левой части и учитывая, что
так как
получим окончательно:
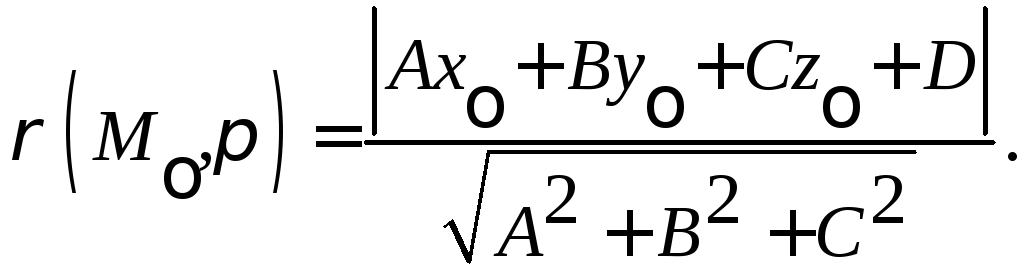(12)
Задача.
Найдите
расстояние между плоскостями:
и
§4. Прямая в пространстве.
4.1. Различные уравнения прямой в пространстве.
4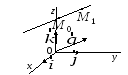
.1.1.
Канонические уравнения прямой в
пространстве.
Положение прямой однозначно определяется,
если
известна одна её точка
и
направляющий вектор
По
этим данным составим уравнения прямой.
Возьмем
на прямой произвольную точку
Векторы
и
коллинеарны,
отсюда:
(13)
Это канонические уравнения прямой в пространстве.
4.1.2. Уравнения прямой, проходящей через две точки.
Две
точки
прямой определяют её направляющий
вектор
.
По формуле (13) получим искомые уравнения:
(14)
4.1.3. Параметрические уравнения прямой.
Они получаются из канонических:
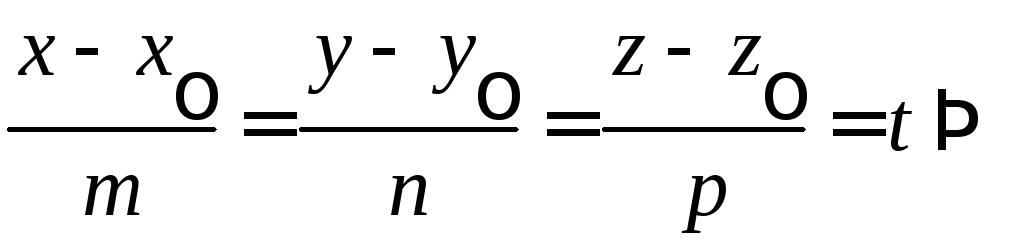
(15)
Задавая
параметру
различные значения, получим координаты
различных точек прямой.
4.1.4. Общие уравнения прямой.
Прямая может быть получена как линия пересечения двух плоскостей:
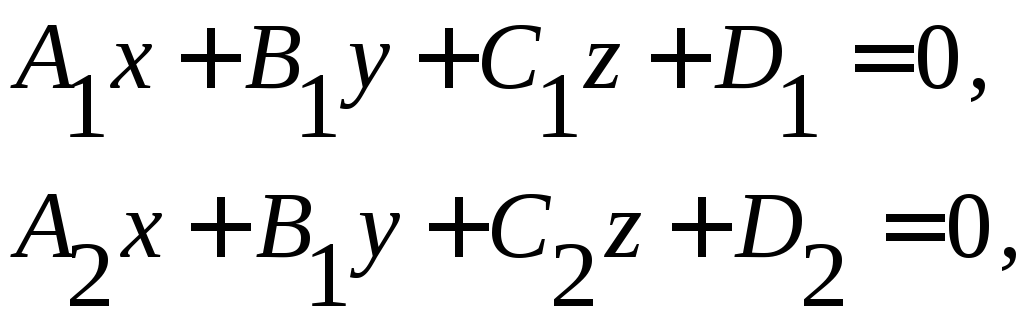(16)
если
Уравнения (16) называются общими уравнениями прямой в пространстве.
Получим
канонические уравнения этой прямой.
Возьмем на ней какую-нибудь точку
Направляющий
вектор в дпск есть векторное произведение
нормальных векторов данных плоскостей:
Окончательно
получим:
Задача. Определите точку пересечения прямой
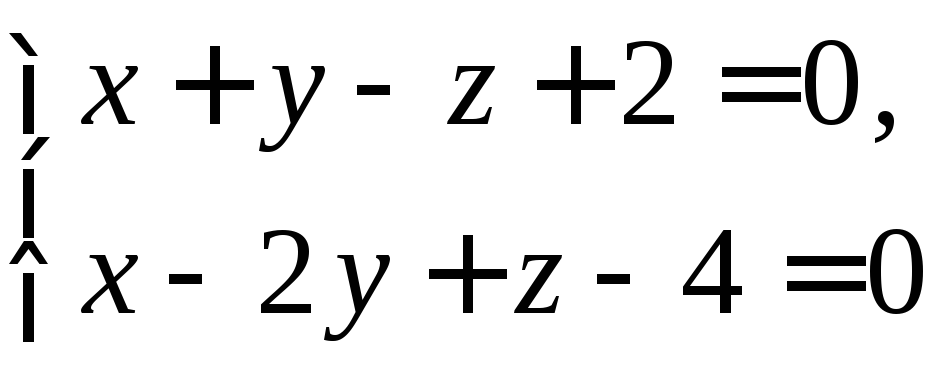с плоскостью
4.2.Взаимное расположение двух прямых.
Зададим
в аффинной системе координат
две прямые:
и
По
направляющим векторам
и вектору
можно определить
взаимное расположение данных прямых. Возможны 4 случая: 1) прямые скрещиваются, 2) прямые пересекаются, 3) прямые параллельны,4)прямые совпадают.
Очевидно, прямые
лежат в одной плоскости тогда и только
тогда, когда векторы
компланарны.
Т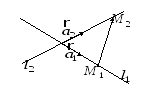
огда
их смешанное произведение равно 0:
=0
(17)
1) Прямые скрещиваются тогда и только
тогда, когда
(18)
2)
Прямые пересекаются тогда и только
тогда, когда они лежат в одной плоскости,
то есть выполнено условие (17), и векторы
коллинеарны.
3) Прямые, лежащие в одной плоскости, параллельны, если они не имеют общих точек. При этом векторы удовлетворяют условиям:
(19)
4) Ясно, что прямые совпадают тогда и только тогда, когда векторы
,
и
попарно
коллинеарны.
Задача 1. Определите взаимное расположение прямых
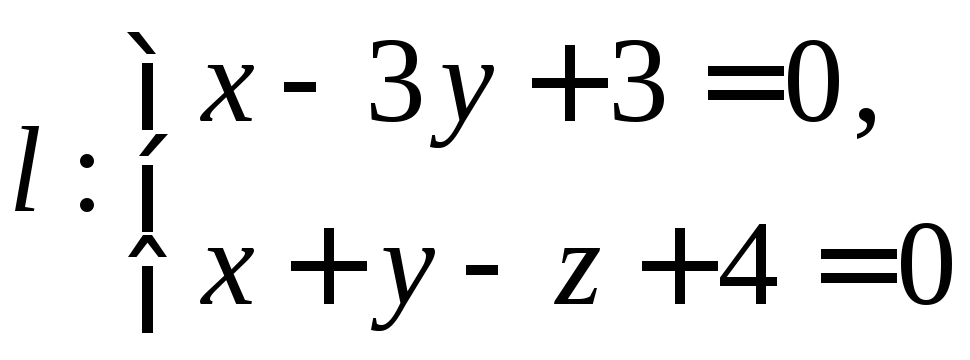и
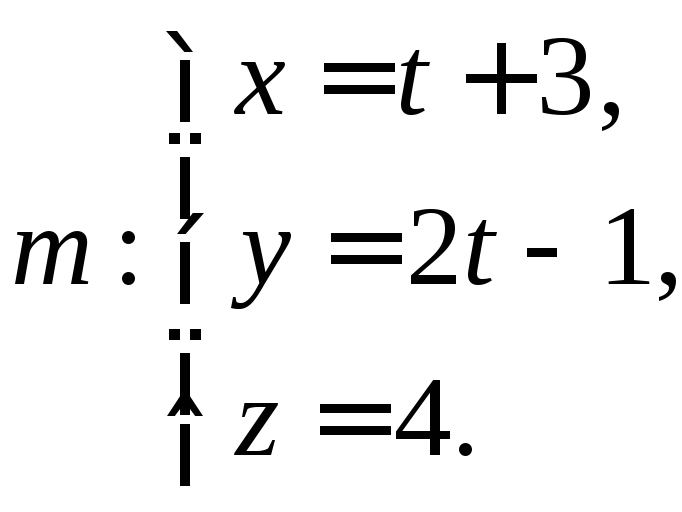
Задача
2. Напишите
уравнения прямой, проходящей через
точку
и пересекающей прямые:
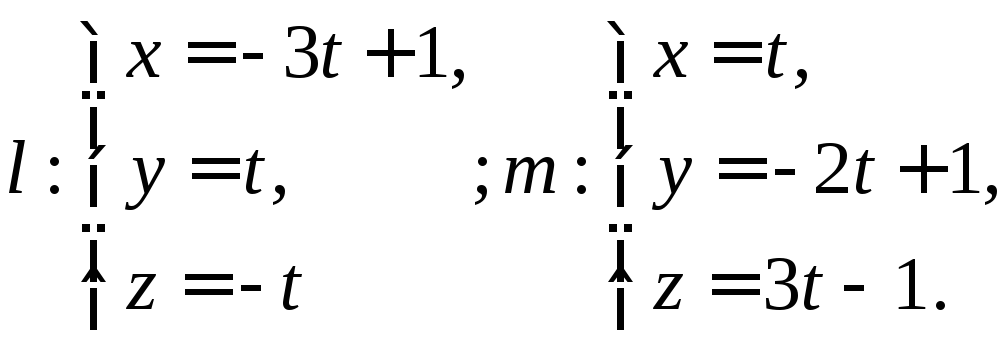
4.3. Взаимное расположение прямой и плоскости.
Зададим в аффинной системе координат прямую
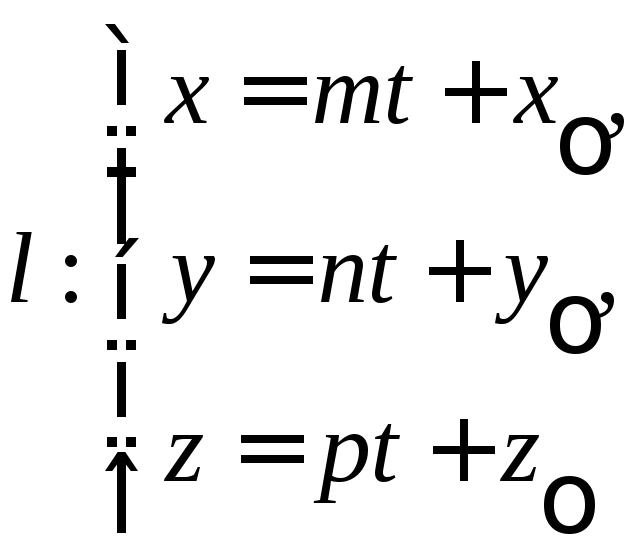(20)
и плоскость
(21)
Будем искать общие точки прямой и плоскости. Для этого нужно решить систему уравнений (20) и (21):
Обозначим:
(22)
Возможны следующие случаи.
1)
Система (20),(21) имеет единственное решение
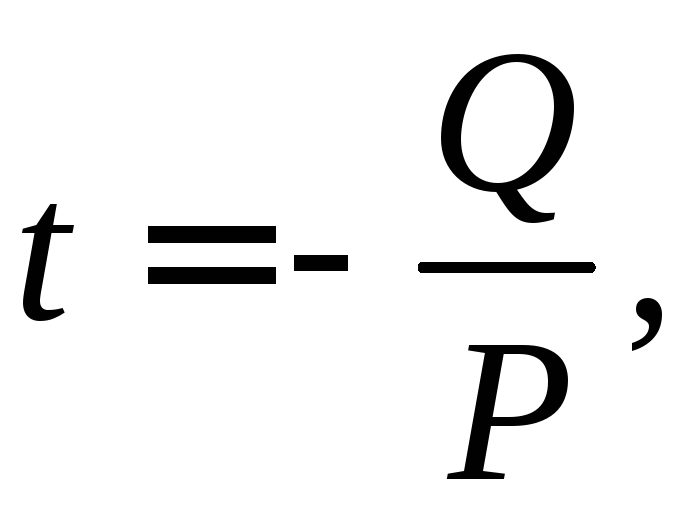
Прямая пересекает плоскость.
Решая систему (20),(21), найдем точку пересечения прямой и плоскости.
2)
Система не имеет решений, если
Причем,
так как
Прямая
и плоскость параллельны.
3)
) Система (20),(21) имеет бесконечно много
решений
Прямая принадлежит
плоскости.
Задача.
Определите
взаимное расположение прямой
и плоскости
4.4.Прямая
линия в системе координат
.
4.4.1. Угол прямой с плоскость.
О
пр.
Углом прямой с плоскостью называется
острый угол между этой прямой и её
проекцией на плоскость.
Зададим
в системе координат
прямую
и плоскость
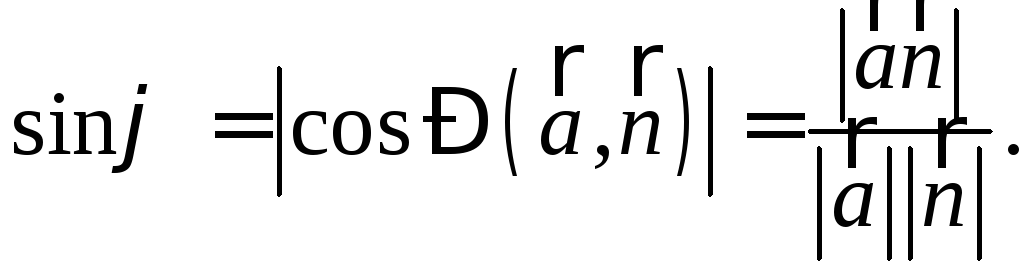(22)
Условие параллельности прямой и плоскости:
Условие перпендикулярности прямой и плоскости:
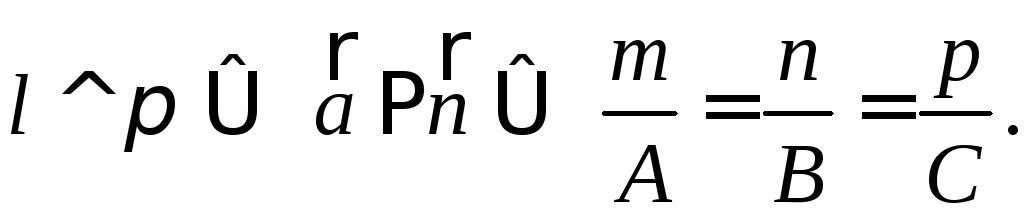
4.4.2. Угол между двумя прямыми.
Угол между двумя прямыми в пространстве определяется как угол между прямыми, параллельными данным и проходящим через одну точку. Его величину можно найти как угол между направляющими векторами прямых. Пусть заданы две прямые:
;
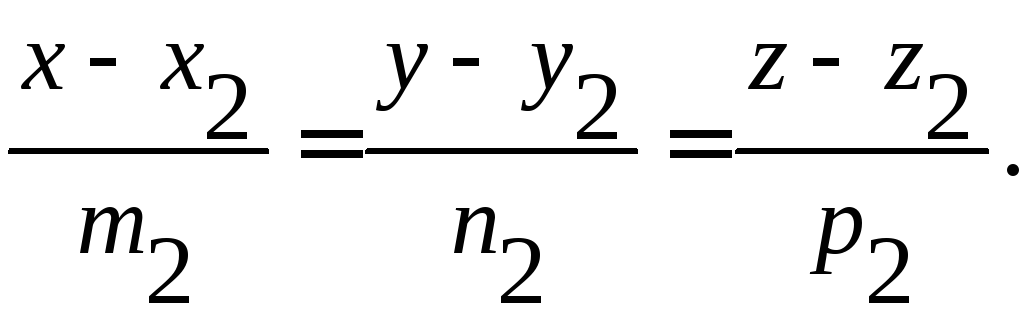
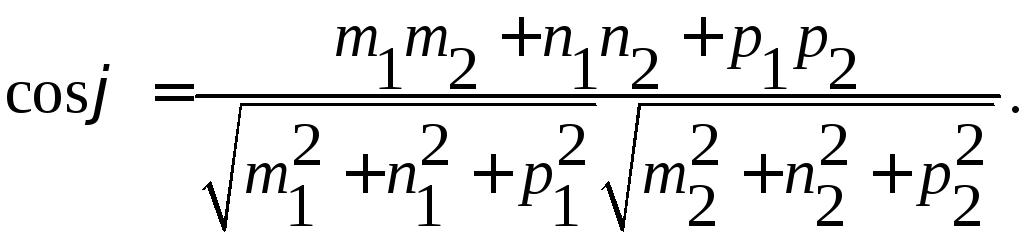
Задача
1. Найдите
точку, симметричную точке
относительно плоскости
Задача
2. Найдите
точку, симметричную точке
относительно прямой
Задача
3. Найдите
расстояние от точки
до прямой
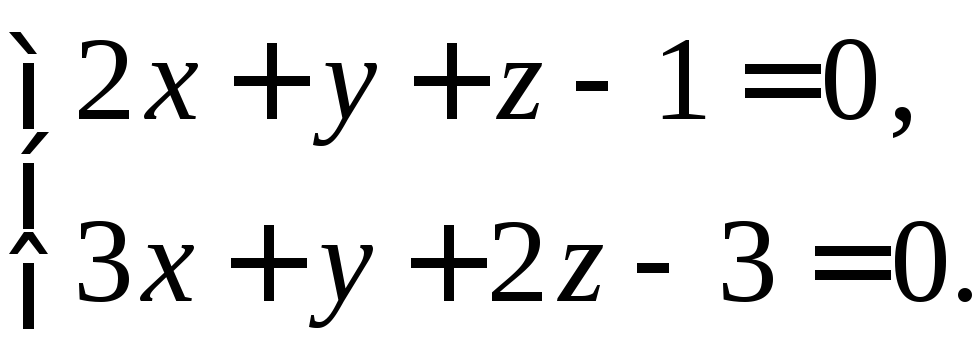
Задача 4. Найдите расстояние между диагональю куба с ребром 1 и не пересекающей её диагональю грани.
Задача 5. Составьте уравнения общего перпендикуляра двух скрещивающихся прямых
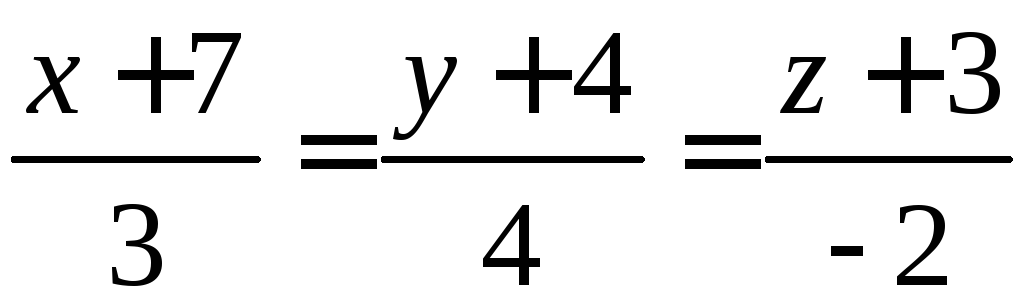и
