Раздел 3. Система координат в пространстве

§1. Плоскость

1. Различные уравнения плоскости

1.1.1.Параметрические уравнения плоскости.

Положение плоскости в пространстве

определим заданием

точки и двух неколлинеарных

векторов которым плоскость

параллельна:

Если точка то векторыкомпланарны. Тогда

(1)

Если на плоскости взять аффинную систему координатто- координаты точки

Пусть

Из соотношения (1) имеем:

(2)

Из (1) следует (2), и наоборот.

Уравнения (2) называются параметрическими уравнениями плоскости.

1.1.2. Уравнение плоскости, проходящей через 3 точки.

Зададим в аффинной системе 3 неколлинеарные точки Они определяют единственную плоскостьДля произвольной точкиплоскости выполняется условието есть

(3)

1.1.3. Уравнение плоскости «в отрезках»

Возьмем, в частности, в качестве точек точки пересечения плоскости с осями координат

Уравнение (3) принимает вид:

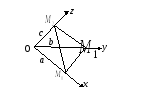
уравнение «в отрезках» 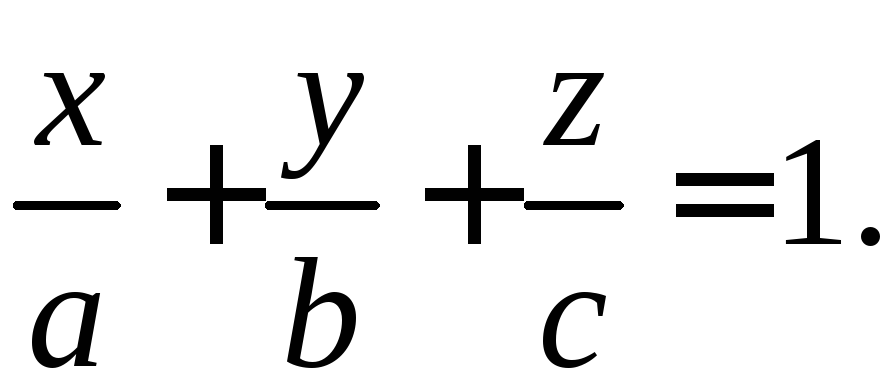(4)

1.1.4..Общее уравнение плоскости.

Зададим плоскость точкой и двумя неколлинеарными векторами:Еслипроизвольная точка плоскости, то векторы

компланарны

где

(5)

где

Очевидно, в дпск вектор

Как видно, в аффинной системе координат плоскость определяется уравнением 1-ой степени относительно трех переменных. Справедливо и обратное утверждение: при уравнение первой степени относительно 3-х переменныхв аффинной системе координат определяет плоскость.

1.1.5.Условие параллельности вектора и плоскости.

Теорема. Для того, чтобы в аффинной системе координат вектор

был параллелен плоскости

необходимо и достаточно, чтобы выполнялось условие

(6)

∆ 1. Пусть Если точкаито точкато есть справедливы равенства:

Вычитая из второго третье, получим:

2. Если выполнено условие (6) и точка то, если

, из

▲

1.1.6. Неполные уравнения плоскости. Построение плоскости по

уравнению.

Уравнение где ни один из коэффициентов не равен 0, называется полным. Для построения плоскости его лучше записать «в отрезках»:

Пример. Постройте плоскость

Обратимся к неполным уравнениям, заданным в аффинной системе координат

1.

Пример. Постройте плоскость

2. Векторпараллелен плоскостиеслиипроходит через ось

если

Пример. Постройте плоскость

3. еслиипроходит через осьесли

Пример. Постройте плоскость

4. Если то плоскость параллельна осии проходит через эту ось, если

5. Плоскостьпараллельна плоскости

6. Плоскостьпараллельна плоскости

7. Плоскостьпараллельна плоскости

8. ПлоскостьЭто координатная плоскость

9. Это плоскость

10. Это плоскость

1.1.7. Геометрический смысл знака многочлена

Пусть в аффинной системе координат задана плоскостьКоординаты точек, принадлежащих этой плоскости обращают это уравнение в верное тождество. Плоскость делит пространство на два подпространства. Можно доказать, что для координат точек одного подпространства Значение многочленаесть положительное число (именно для того подпространства, где находится вектор), а для точек другого подпространства – отрицательное.

Задача. Определите взаимное расположение точек относительно плоскости