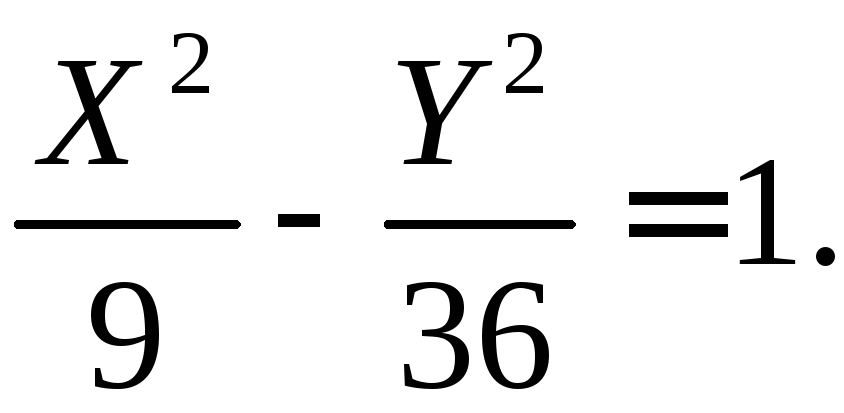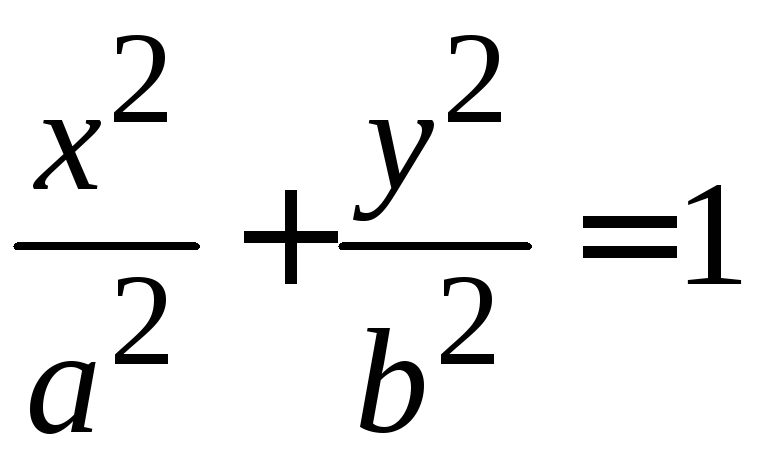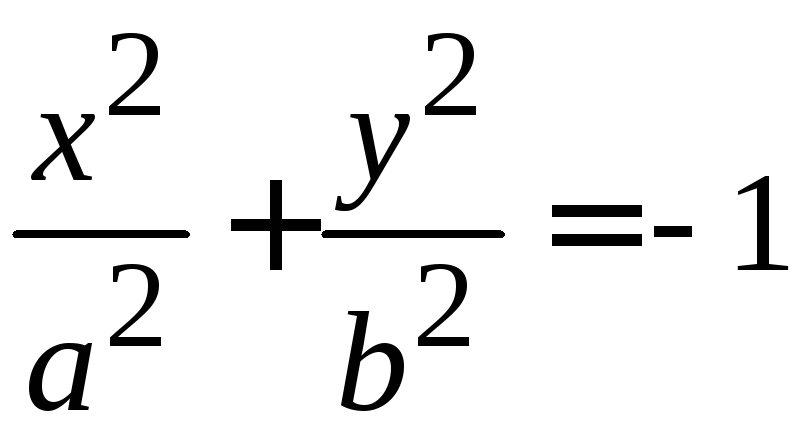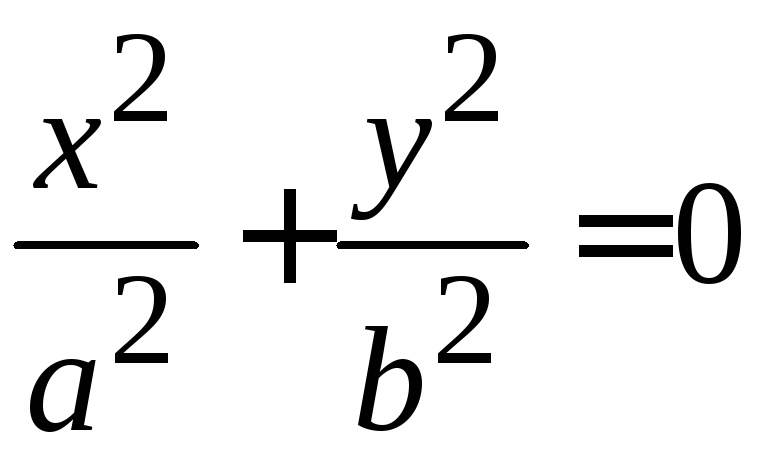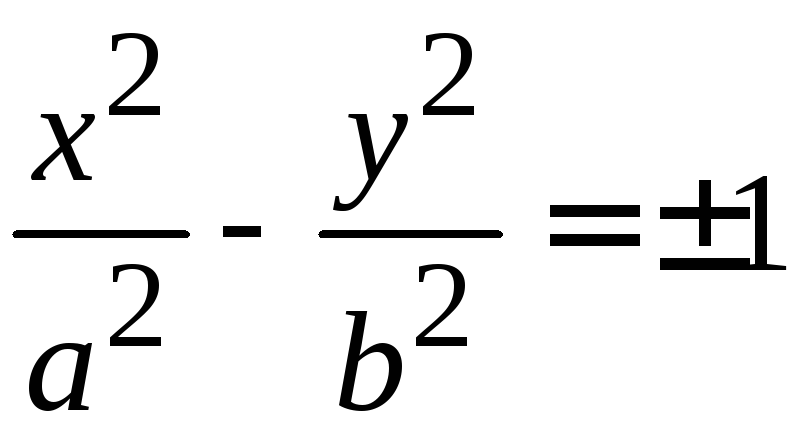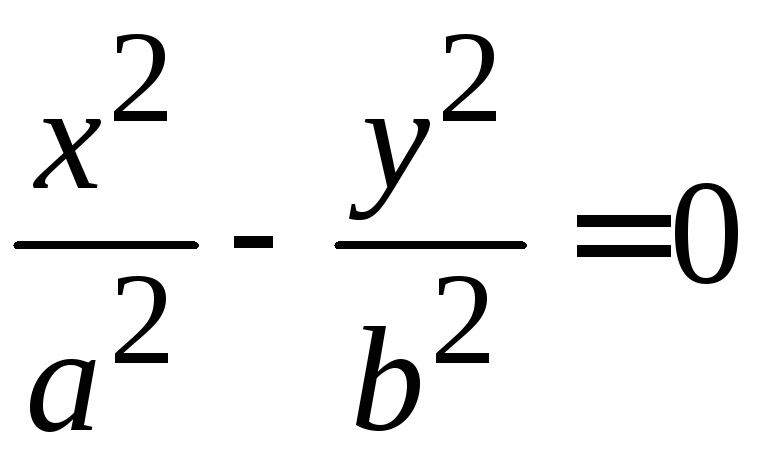Часть 2. Исследуем уравнение (17):

Случай 1.

Преобразуем уравнение (17), выделяя полные квадраты.

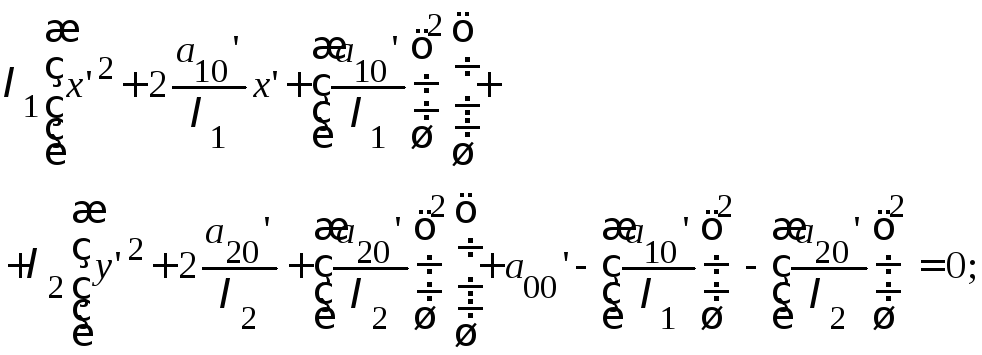
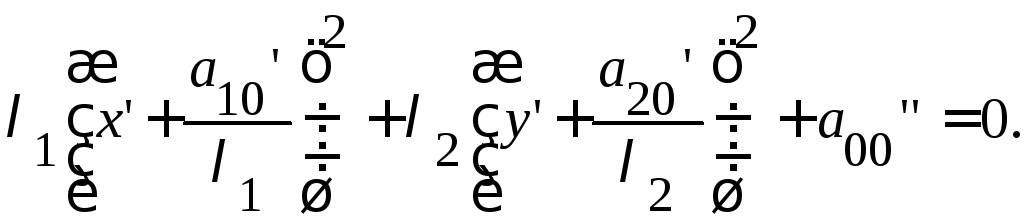(18)

Перенесем начало координат в точку 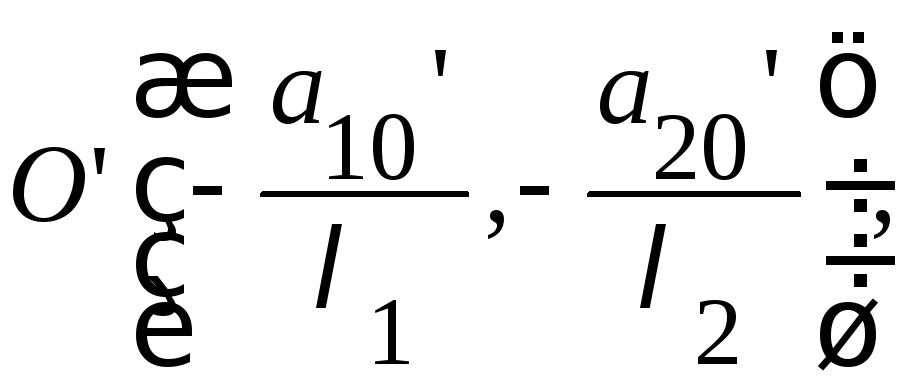то есть выполним преобразование «перенос начала координат»:

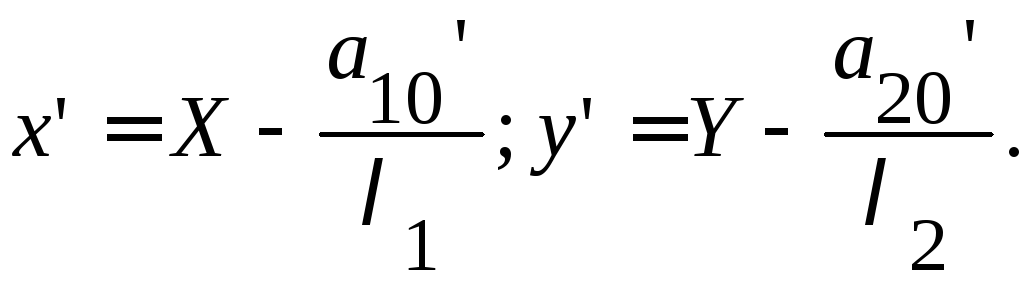
Уравнение (18) примет вид:

(19)

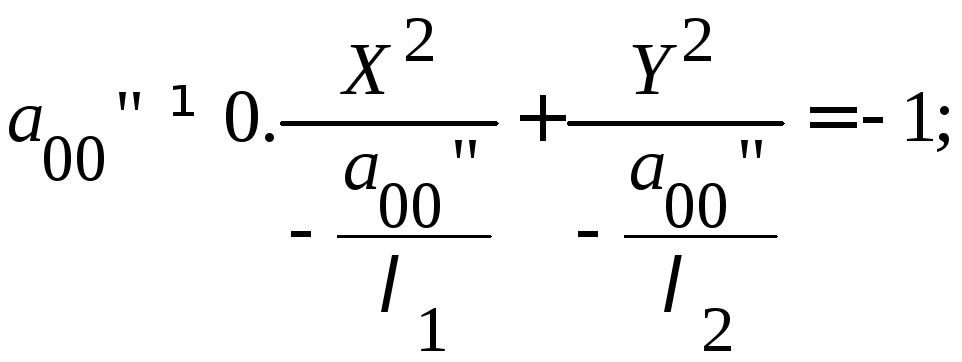а) б)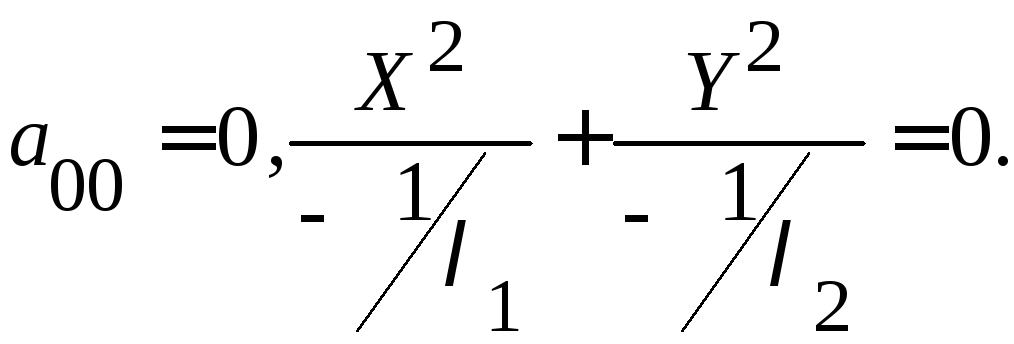

Вывод. Если корни характеристического уравнения не равны 0, то линия 2-го порядка является линией одного из следующих видов:

№				Каноническое уравнение	Название линии
1.	+ -	+ -	- +		Эллипс
2.	+ -	+ -	+ -		Мнимый эллипс
3.	+ -	+ -	0 0		Точка пара мнимых прямых, пересека- ющихся в этой точке
4.	+ -	- +			Гипербола
5.	+ -	- +	0 0		Пара пересекающихся прямых

Случай 2.

(17)

(17)

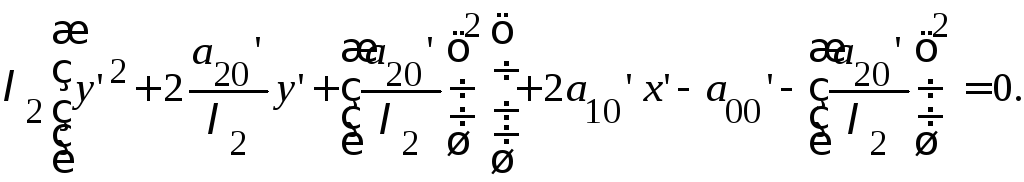
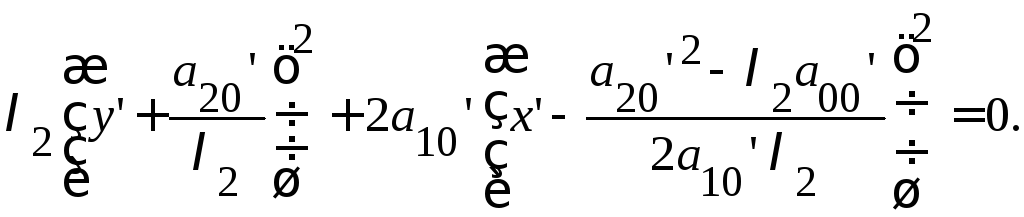
Перенос начала в точку

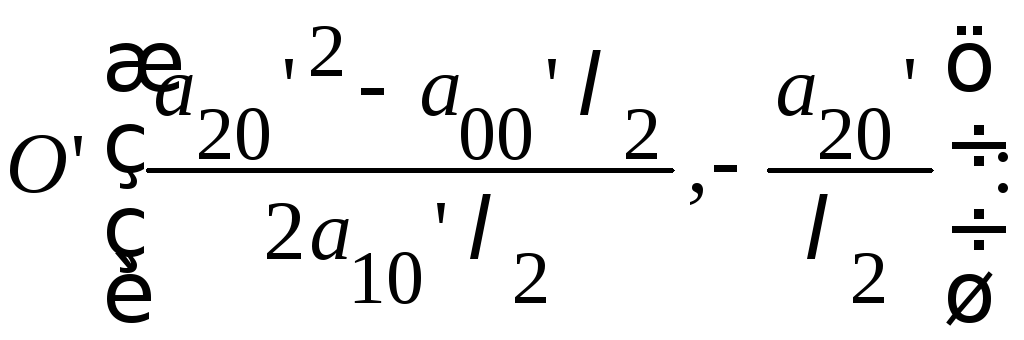
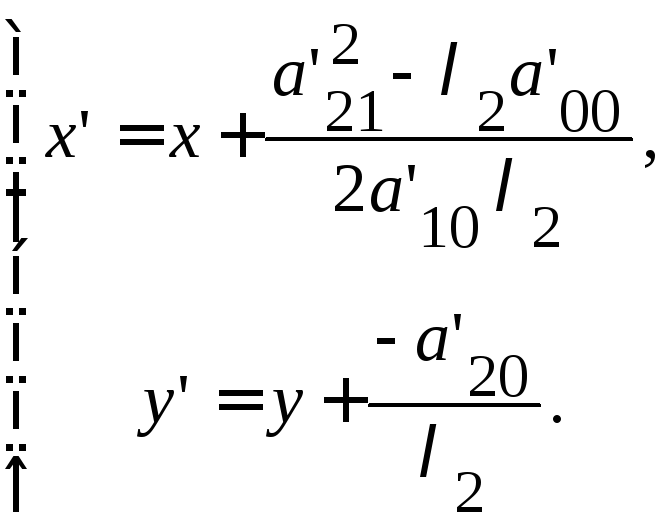
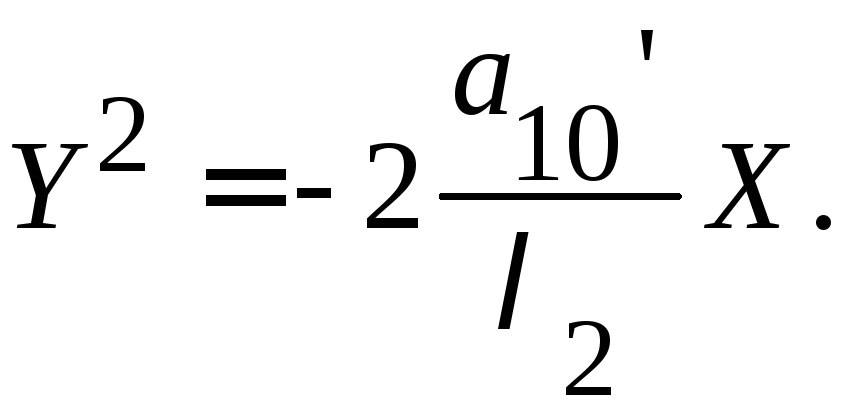
В случае получим уравнение параболы:

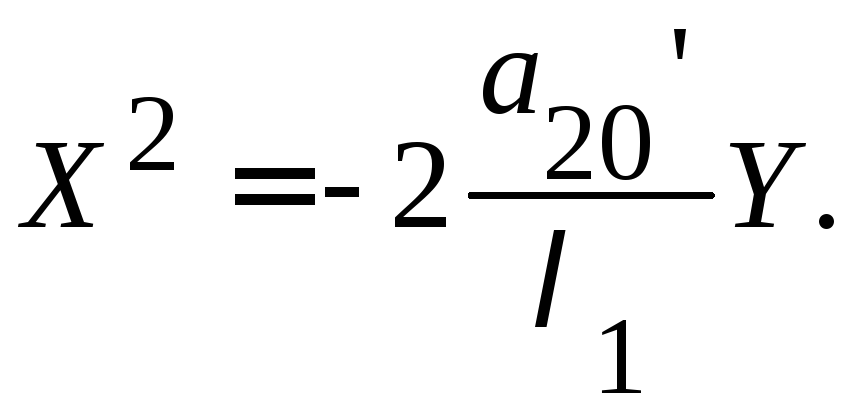
Случай 3.

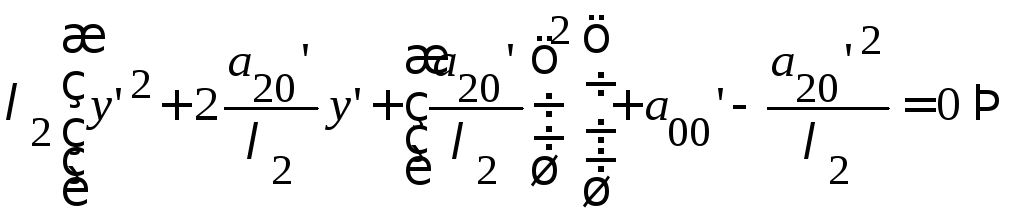
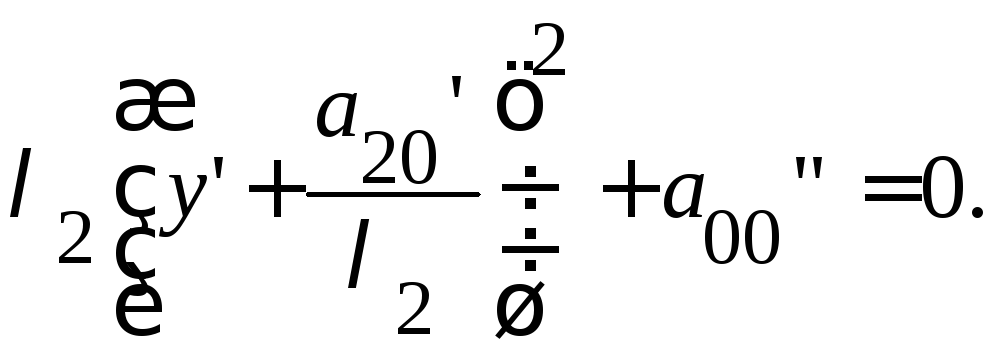Параллельный перенос в точку 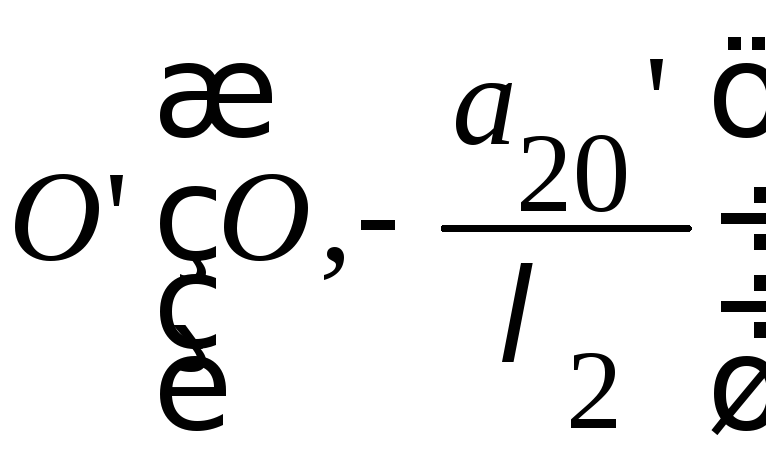преобразует уравнение: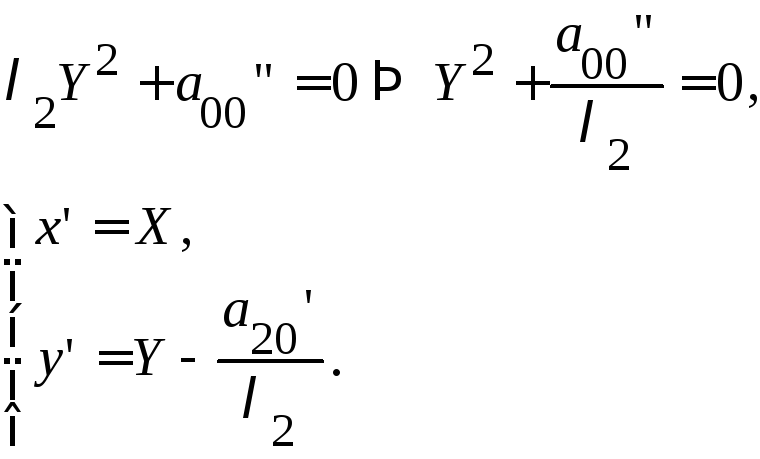

а) 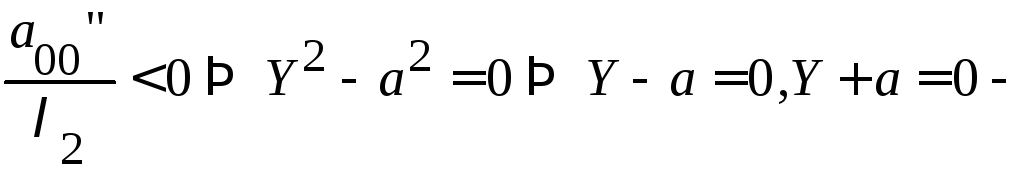две

действительные параллельные прямые.

б) 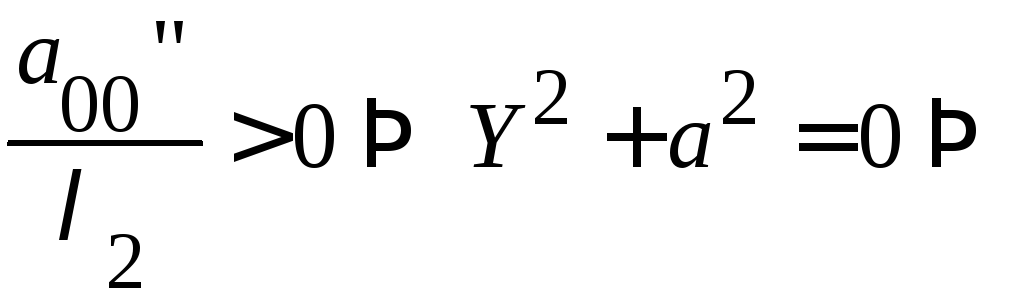две мнимые параллельные прямые.

в) 2 совпавшие прямые.

Вывод: уравнение (11) определяет одну из 9-ти линий:

1. эллипс,

2. гипербола,

3. парабола,

4. мнимый эллипс,

5. пара пересекающихся прямых,

6. пара параллельных прямых,

7. пара совпавших прямых,

8. пара мнимых прямых, пересекающихся в действительной точке,

9. пара мнимых параллельных прямых.

Алгоритм приведения общего уравнения линии

2-го порядка к каноническому виду

1. Составим характеристическое уравнение:

и найдем его корни.

2. Совершим поворот данной системы координат на уголопределяемый по формуле:

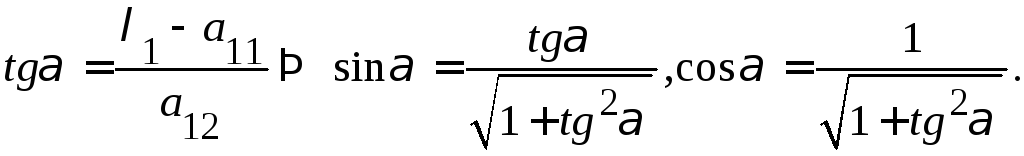
Формулы преобразования координат: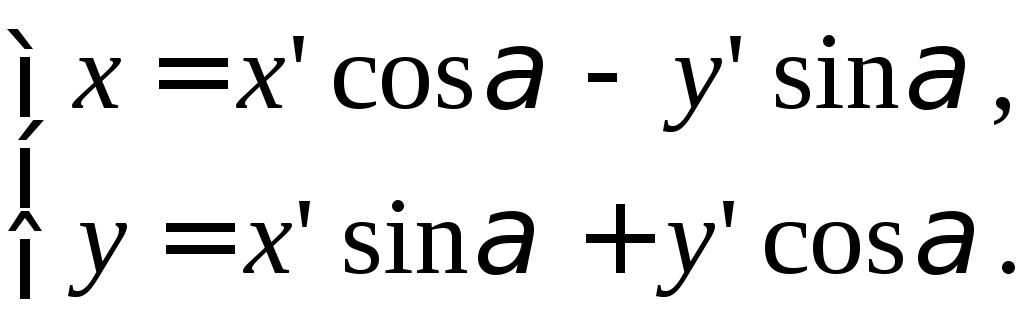

3.Запишем уравнение кривой в новой системе координат

(*)

где

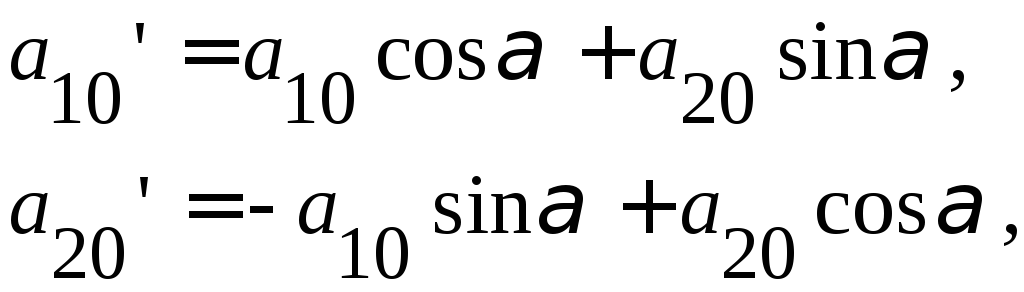
4.Совершив параллельный перенос системы координат, получим из уравнения (*) каноническое уравнение кривой в системе

5. Построим системы ии по каноническому уравнению данную

линию.

Пример. Преобразованием прямоугольной системы координат приведите уравнение линии второго порядка к каноническому виду.

Решение

1. Запишем и решим характеристическое уравнение кривой:

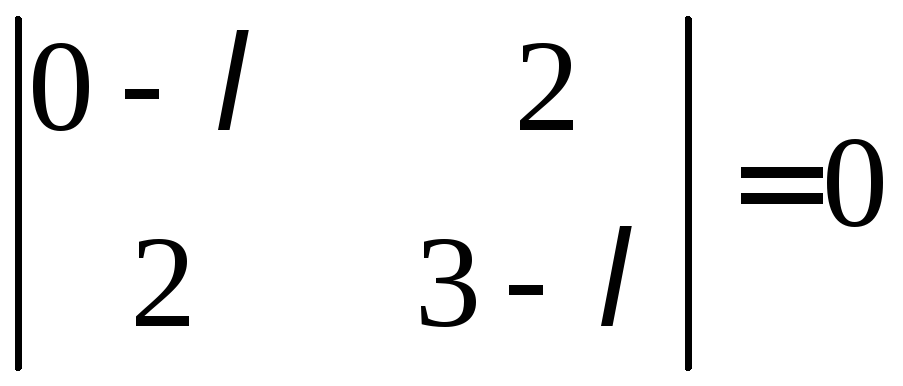, отсюда

2. Находим угол поворота системы координат:

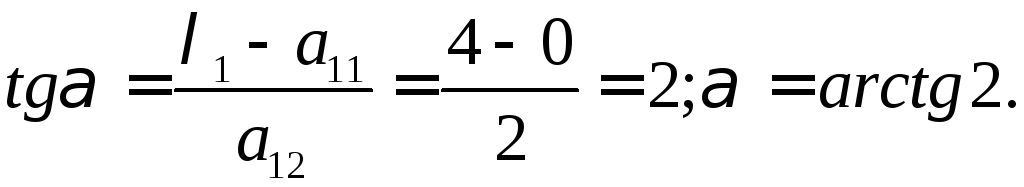
Тогда cos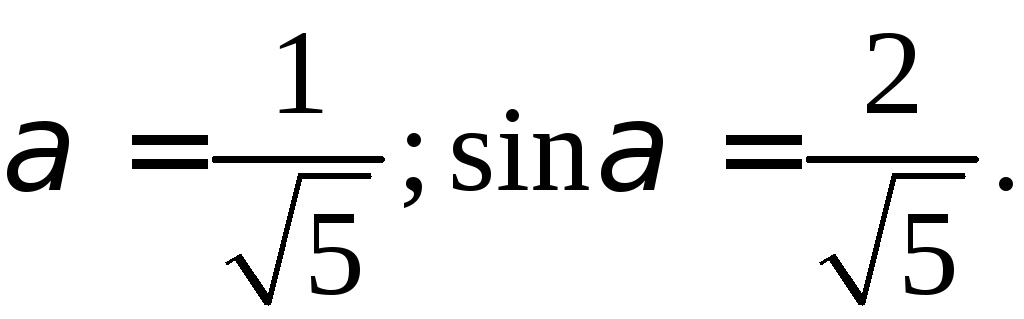

3. Запишем формулы преобразования координат при повороте системы координат на угол

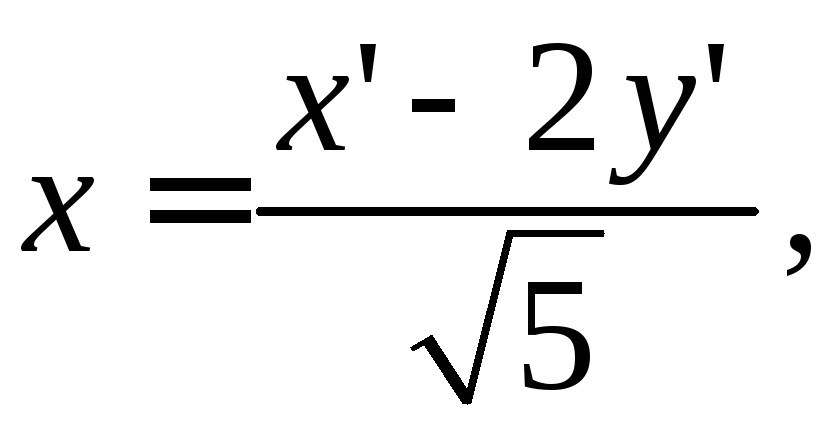
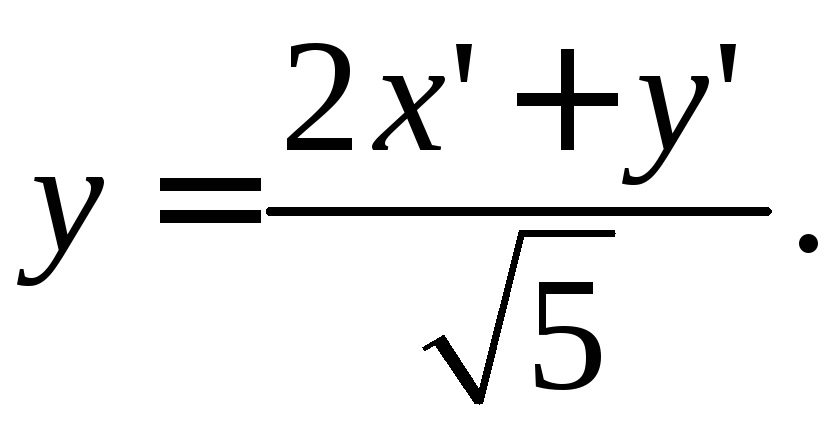
4. После поворота осей координат уравнение линии запишется в виде:

Найдем коэффициенты и

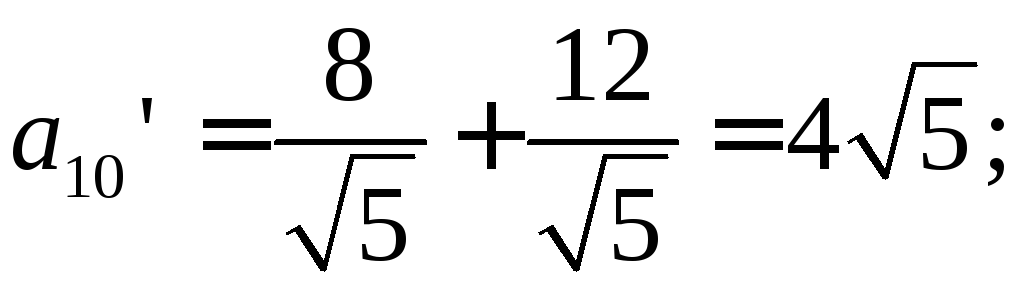
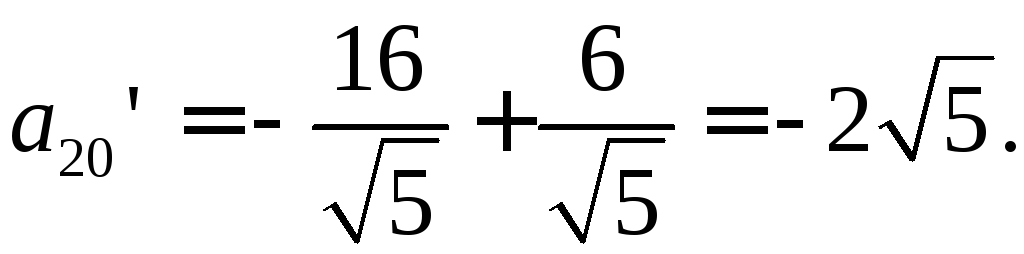
Уравнение принимает вид:

5.Преобразуем уравнение, используя параллельный перенос осей в новое начало.

Выполним параллельный перенос системы координат в точку

Уравнение кривой запишется в виде: или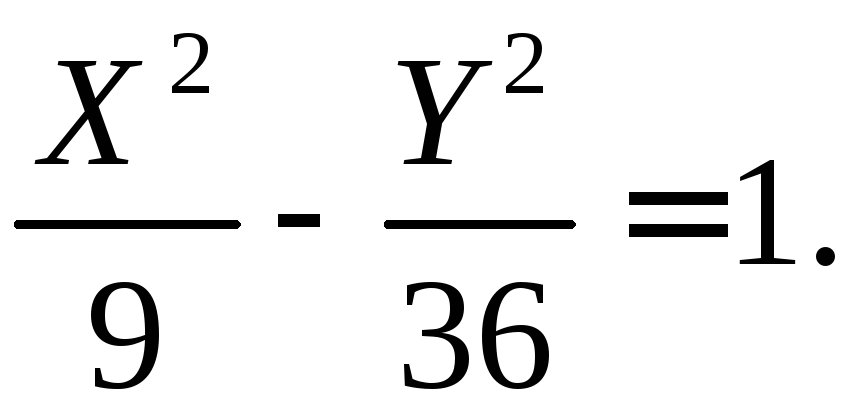

Получили каноническое уравнение гиперболы.

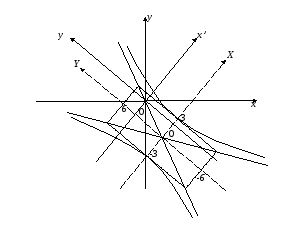
Построение графика

1. Строим исходную систему координат Оху.

2. Поворачиваем Оху на угол ,

получим систему О

3. Переносим параллельно в точку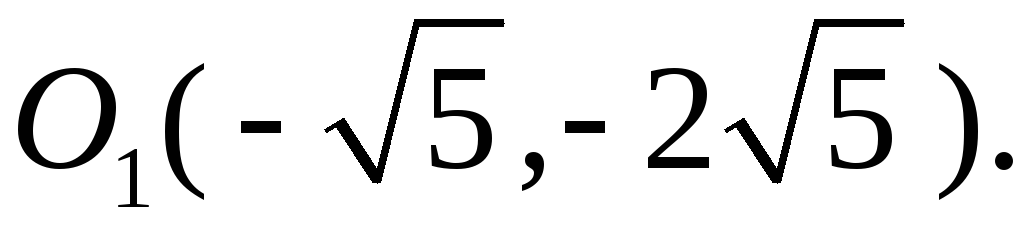

Получим систему

4. В последней системе строим гиперболу