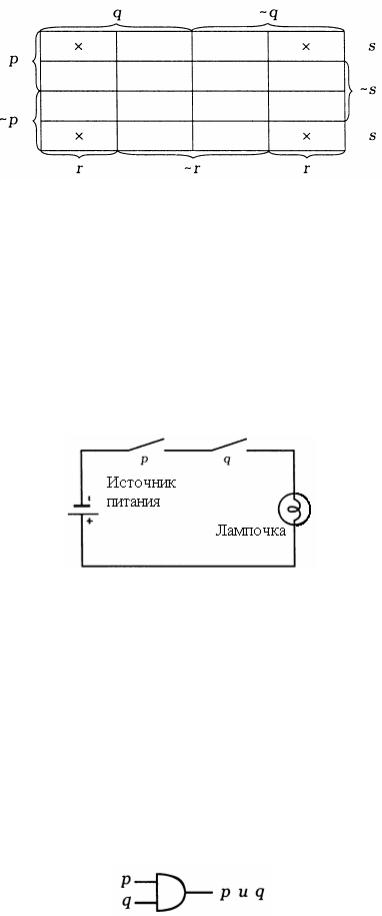
можно описать посредством r s .

Наглядный способ поиска минтермов для группировки, который предоставляет карта Карно, можно обобщить на булевы функции пяти и даже шести переменных. Однако, возникающие при этом «трехмерные» диаграммы, вносят в метод дополнительные осложнения и делают его малопроизводительным.

5.3 Функциональные схемы

В 1938 г. Клод Шеннон заметил связь между таблицами истинности и электрическими цепями. Рассмотрим схему переключения, приведенную на следующем рисунке

Она состоит из источника питания, двух переключателей и электрической лампочки. Присвоим значение 1 переключателям р и q, если они замкнуты, т.е. электрический ток проходит через них. Если переключатель разомкнут, то считаем, что переключателю (точнее булевой переменной) присвоено значение ноль. Присвоим значение 1 схеме, когда лампочка светится (т.е. электрический ток через нее проходит). При последовательном соединении элементов цепи р и q лампочка загорается, и значение схемы становится равным 1 только в случае, когда оба переключателя замкнуты, т.е. и р и q имеют значение 1. Таким образом, схема соответствует булеву выражению p q (или p q ). В этом параграфе удобнее использовать обозначения

логических операций +, и ‘ (штрих). Такое расположение переключателей

называется логическим элементом р И q, или схемой логического умножения. Этот логический элемент обозначается следующим символом

Теперь рассмотрим схему переключения, показанную на следующем рисунке, где переключатели р и q соединены параллельно.

14

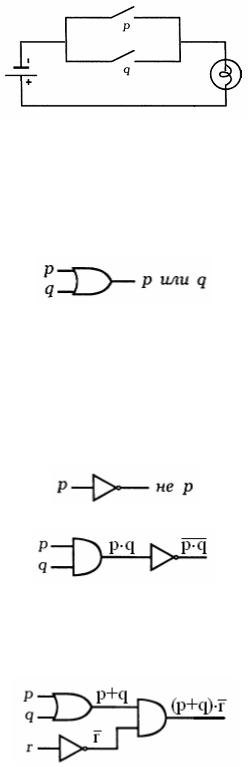
Отметим, что теперь лампочка загорается, и значение схемы становится равным 1, когда один (или оба) из двух переключателей р или q замкнут, т.е. либо значение р = 1, либо q = 1 (либо оба они равны 1). Эта схема соответствует высказыванию p + q и называется логическим элементом p ИЛИ q, или схемой логического сложения. Этот логический элемент обозначается следующим символом

Предположим, имеется схема, с одним переключателем р, который обладает таким свойством, что лампочка загорается тогда и только тогда, когда р разомкнут. Следовательно, схема имеет значение 1, когда р имеет значение 0, и имеет значение 0, когда р имеет значение 1. Эта схема соответствует отрицанию p, т.е. р', а соответствующий элемент называется логическим элементом не, или инвертором. Логический элемент не обозначается следующим символом

Пример 1. Схема на следующем рисунке

содержит логический элемент р и q, за которым следует инвертор, так что схема соответствует выражению (p q)' . Заметим, что инвертор отрицает всю

предшествующую ему схему.

Пример 2. Схема на следующем рисунке

содержит соединение логического элемента р или q с логическим элементом не r посредством логической схемы умножения. Следовательно, она соответствует выражению (p + q) r' .

Пример 3. Булево выражение, соответствующее схеме на следующем рисунке, имеет вид (p' q)+ (p r')'

15

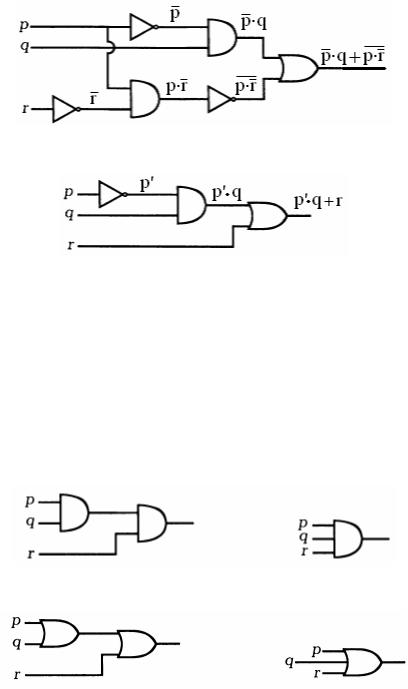
Пример 4. Схема, соответствующая выражению (p' q)+ r , показана на следующем рисунке.

Пример 5. Построим схему трехклавишного переключателя, при помощи которого свет включается тремя различными двухпозиционными переключателями. Для этого построим соответствующее ему булево выражение. Свет должен включаться, когда все три переключателя замкнуты, т.е. необходимо иметь p q r . Если один из переключателей разомкнут, то

свет должен быть выключен. Однако, если разомкнуть другой переключатель, то свет должен включиться. Следовательно, искомое выражение имеет вид p q r + p q' r'+p' q' r + p' q r' . Для простоты, вместо

схемы, представленной на следующем рисунке слева, для выражения p q r будем использовать схему, изображенную на рисунке справа.

А для выражения р+q+r вместо схемы, показанной на следующем рисунке слева, мы будем использовать схему, показанную справа.

Аналогично будем изображать схемы с большим количеством входных сигналов, т.е. правые схемы на предыдущих рисунках могут иметь по четыре и более входных линий, и будут соответствовать левым схемам с однотипными элементами (только И или только ИЛИ). Используя такие сокращающие значки, искомая схема примет вид

16

□

Ранее было отмечено, что штрих Шеффера, обозначаемый |, имеет ту же таблицу истинности, что и (p q)' , поэтому мы и упоминали его как

логическую связку не-и. В свою очередь, стрелка Пирса ↓, имеет ту же самую таблицу истинности, что и (p + q)' , поэтому она упоминалась как

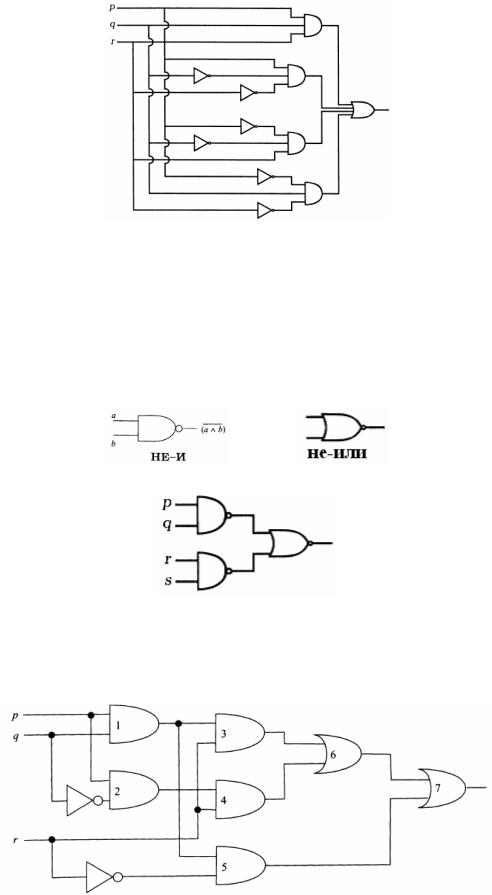
связка не-или. Логические элементы не-и и не-или обозначаются символами, показанными на следующем рисунке, соответственно слева и справа

Тогда, например, выражению (p | q)↓(p | r) соответствует следующая схема

Таким образом, соединяя функциональные элементы вместе, мы получаем функциональную схему. С ее помощью можно реализовать любую булеву функцию.

Пример 6. Что получится на выходе функциональной схемы, представленной на рисунке

В таблице перечислены входы и соответствующие выходы для каждого функционального элемента в соответствии с нумерацией из рисунка

17

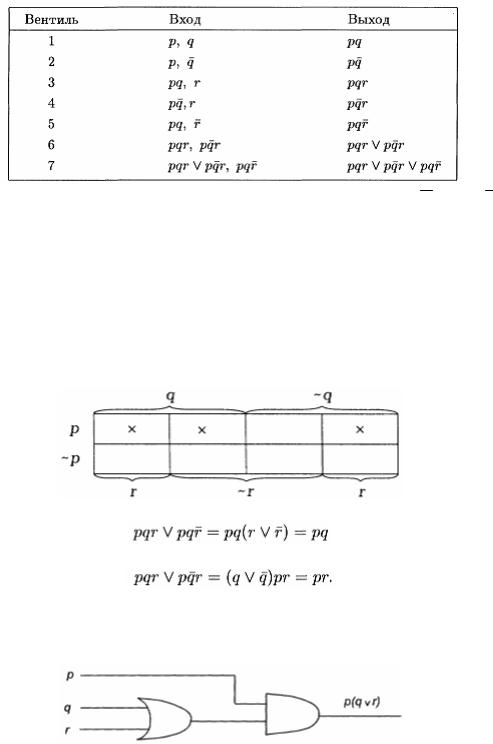
Таким образом, на выходе схемы получится функция p q r p q r p q r .

Как мы видели, диаграммы функциональных схем можно упростить, если разрешить функциональным элементам И и ИЛИ иметь не по два входа, а больше. Но более впечатляющего упрощения можно добиться, если привлечь карту Карно для преобразования функции, полученной на выходе сложной схемы.

Упростим булеву функцию, генерируемую нашей схемой, и найдем более простую функциональную схему, ее реализующую. Карта Карно требуемого выражения представлена на следующем рисунке.

Она имеет две пары минтермов для группировки. Итак,

реализующая булеву функцию, показана на следующем рисунке

□

При вычерчивании функциональных схем нет необходимости использовать все типы функциональных элементов. Как мы уже видели, множество {V,~} является полной системой функций. Поэтому мы можем построить любую схему, ограничившись функциональными элементами И и НЕ. Более того, если по той или иной причине нам неудобно использовать большое число компонент, мы могли бы использовать только функциональный элемент НЕ— И.

Пример 7. Начертим функциональную схему, реализующую булеву функцию p (q r), используя только НЕ—И. Заметим, что

18