§. Критерий Коши сходимости ряда.
Критерий
Коши для сходимости ряда следует из
критерия Коши для сходимости
последовательности частных сумм 
:
.
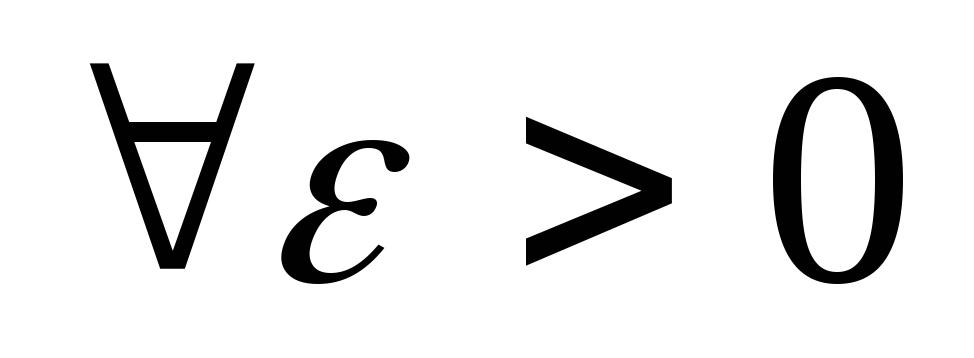
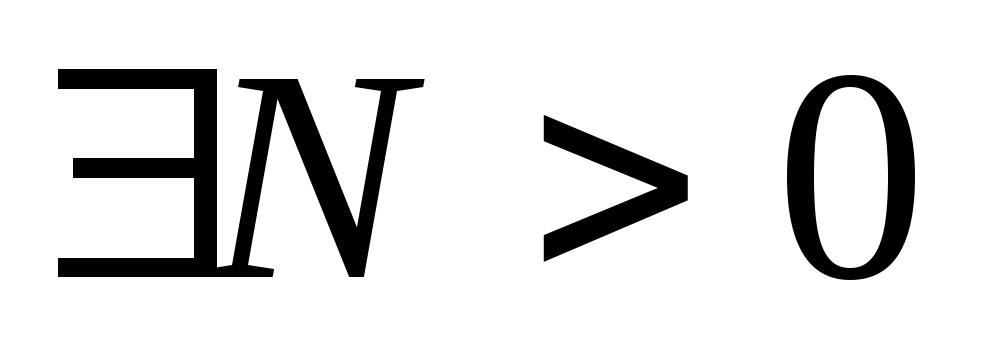
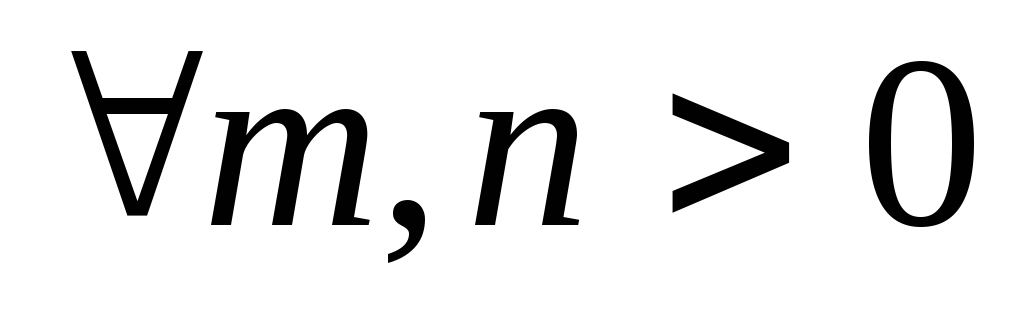
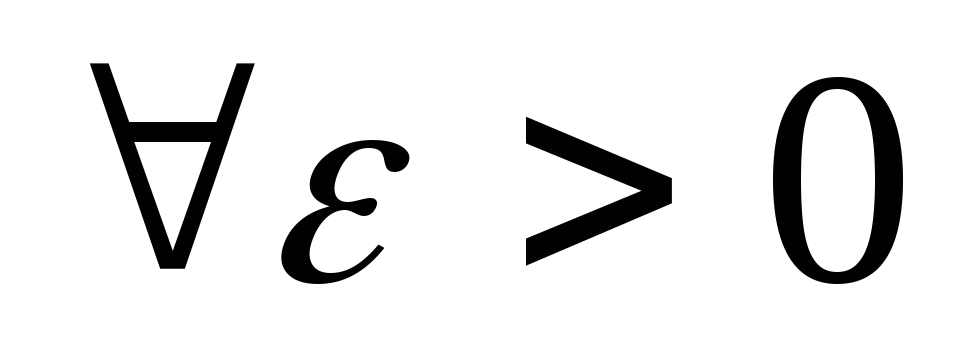
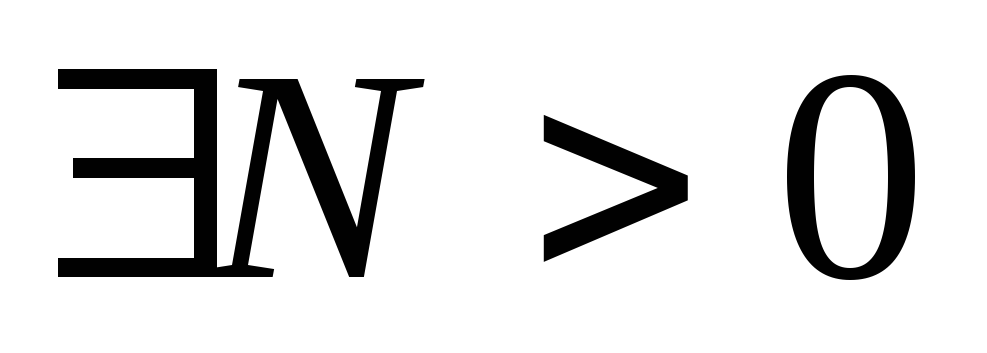
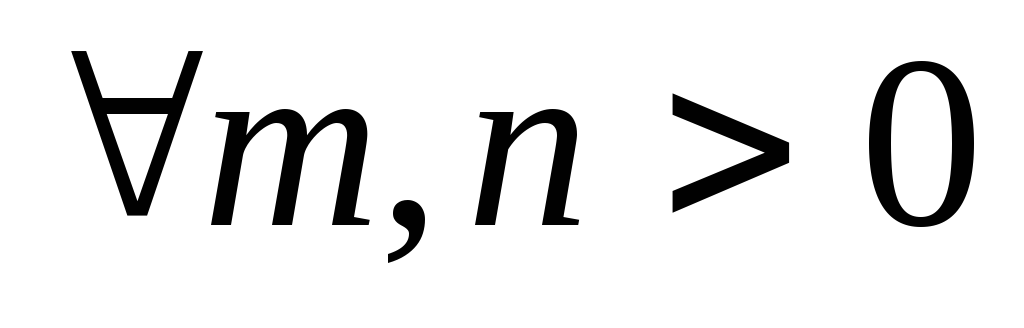
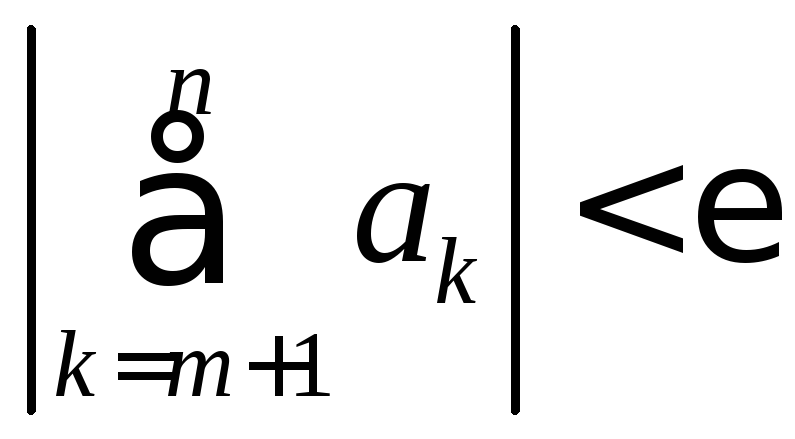Если
ряд сходится то, из критерия Коши при m
= n + 1 следует, что 
т.е. необходимое условие сходимости
ряда:
Если ряд сходится, то его общий член стремится к нулю при n .
Из критерия Коши также следует:
Сходимость ряда не изменится, если в нем изменить, добавить, или изъять любое конечное количество слагаемых. (
)
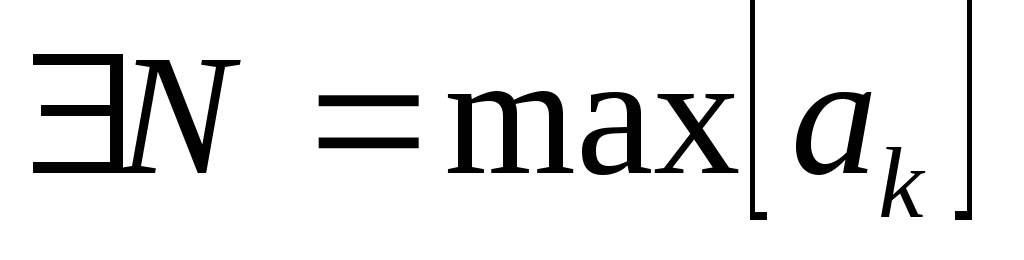Сходимость ряда не изменится, если изъять конечное или нет число нулевых элементов.
Для
ряда 
величина 
называется частной (или частичной)
суммой, а величина 
называется остатком после n-го
члена.
Для
сходящегося ряда остаток 
после n-го члена
необходимо стремится к нулю.
Примеры:
а).
.
При 
=
=
.
т.е. несмотря на то, что общий член ряда стремится к нулю, ряд расходится. Стремление общего члена ряда к нулю это только необходимое условие сходимости ряда, но не достаточное.
б).
;
рассмотрим 
Т.е.
для ряда не выполнен критерий Коши. Ряд
расходится. Этот ряд называется
гармоническим.
в).
;
.
При 
.
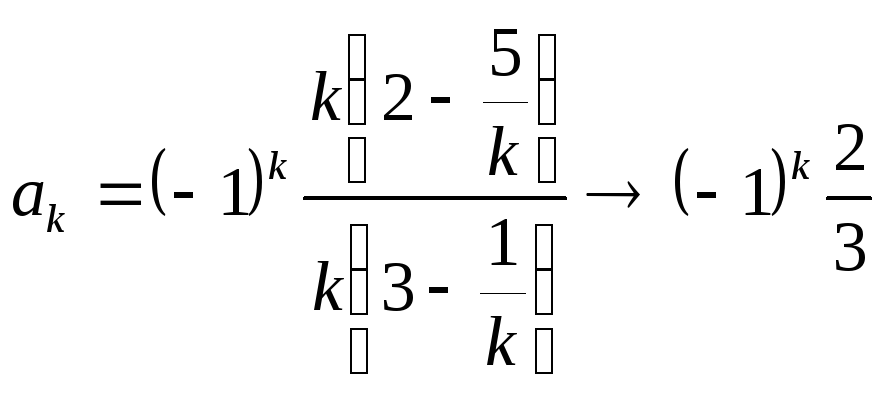Общий член ряда не стремится к нулю. Не выполнено необходимое условие сходимости. Ряд расходится.
г).
;
.
Общий член ряда не стремится к 0. Ряд расходится.
д).
;
не стремится к 0. Ряд расходится.
е).
;
Ряд представляет собой сумму геометрической
прогрессии.
.
– получена формула для нахождения
частичной суммы ряда. 
существует, если |q| <
1. Тогда 
.
Ряд сходится.
§. Абсолютная сходимость.
Def:
Ряд 
называется сходящимся абсолютно, если
сходится ряд 
.
Т. Если ряд сходится абсолютно, то он сходится.
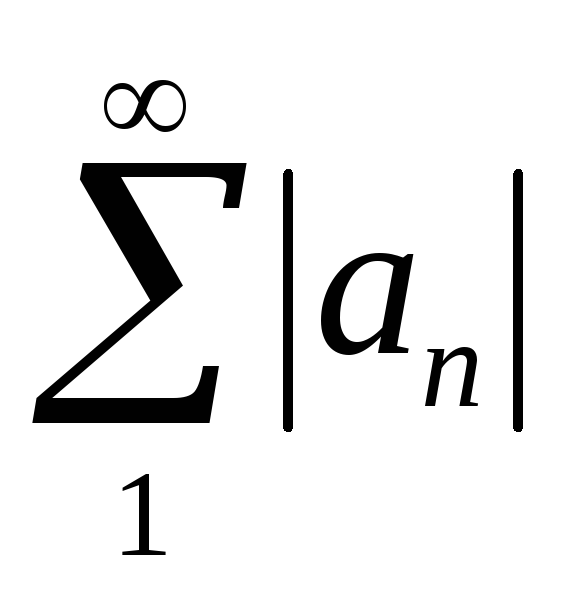–сходится 
.
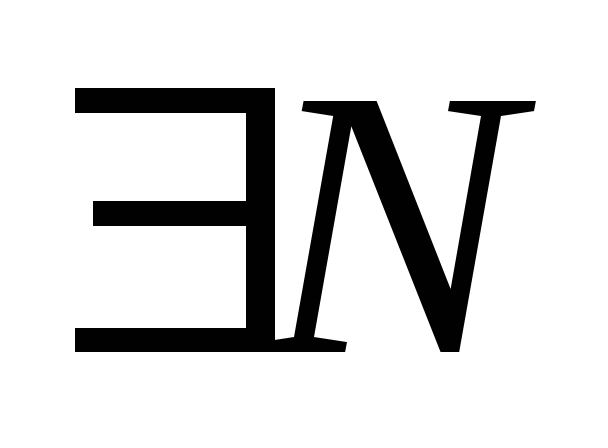
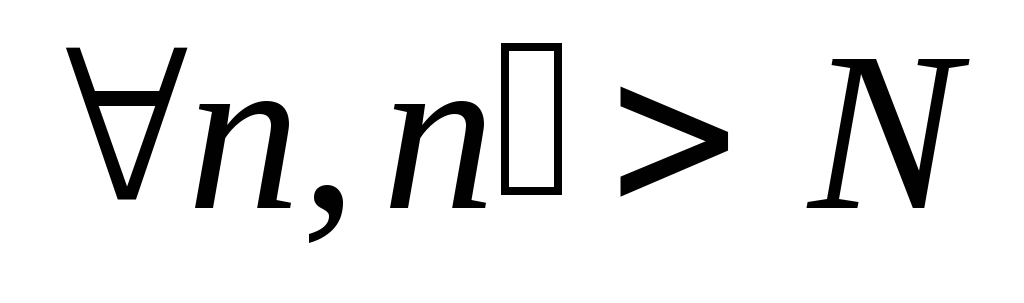
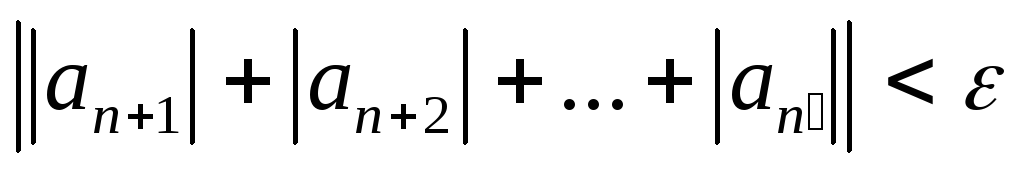Учитывая,
что
получаем
Т.е.
исходный ряд сходится. ▲
Ряд, который сходится, но не сходится абсолютно, называется сходящимся условно.
Замечание:
Если
для ряда 
все его члены не отрицательны, то есть
(
),
то последовательность его частичных
сумм не убывает и, следовательно, для
сходящегося ряда его сумма – это верхняя
грань его частичных сумм.
§. Признаки сходимости знакопостоянных рядов.
а). Мажорантный признак.
Пусть
имеется два ряда с положительными
членами (знакоположительных) 
и 
и
N
n>N
.
Тогда: если ряд 
сходится
–
сходится;
если
ряд 
расходится
–
расходится.
▲.
б).Асимптотическая форма мажорантного признака.
Пусть
n
и, при n,
.
Тогда: сходится 
сходится 
;
расходится
расходится
.
в).Асимптотический признак одновременной сходимости – расходимости рядов.
Пусть
n
при n
.
Тогда ряды 
и
сходятся
или расходятся одновременно.
г).Предельная форма асимптотического признака одновременной сходимости – расходимости рядов
Пусть
n
и существует, конечен и не равен нулю
,
то ряды 
и
сходятся – расходятся одновременно.
§. Интегральный признак Коши – Маклорена.
Т.
Если для знакоположительного ряда с
монотонно убывающими членами, существует
интегрируемая по Риману на замкнутых
подпромежутках положительной полуоси,
невозрастающая неотрицательная функция,
совпадающая при целых значениях аргумента
со значениями соответствующих членов
ряда, то ряд и несобственный интеграл
сходятся и расходятся одновременно.
При этом разность между остатком ряда
после n-го члена и
интегралом по 
не превышает n +1 члена
ряда.
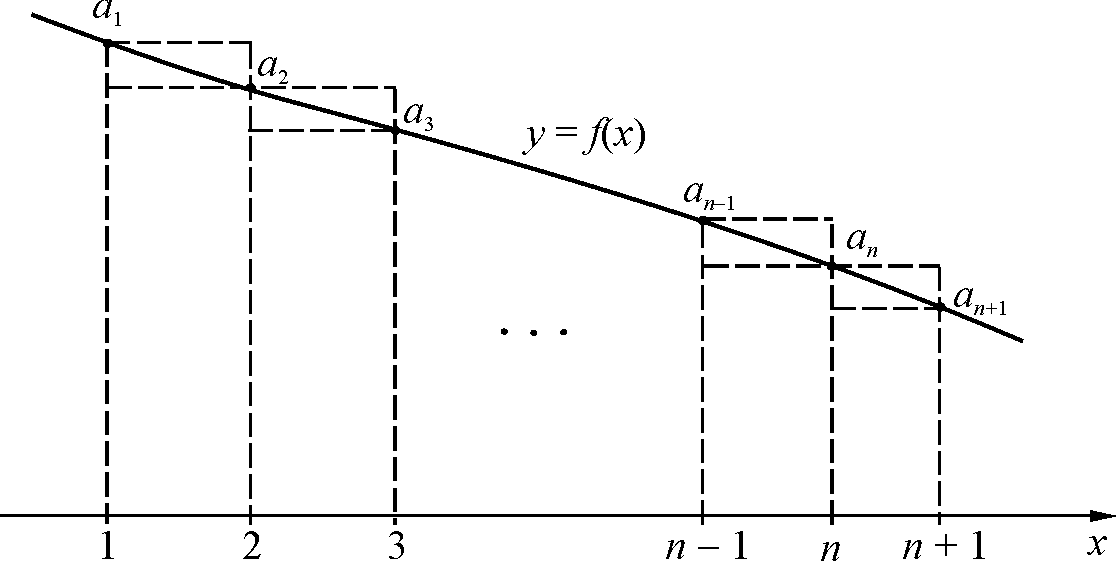
Δ Рассмотрим на оси абсцисс точки 1, 2, 3, …, n–1, n, n +1. И построим …..
П
.
Здесь 
– площадь криволинейной трапеции «по
недостатку», а 
– площадь криволинейной трапеции «по
избытку».
Пусть
такая, что 
и, кроме того, 
.
Тогда
.
Из этого неравенства, ясно что, если
ряд 
сходится,
то сходится и интеграл 
,
и наоборот.
(?).
Рассмотрим цепочку неравенств:
.
Перейдем к пределу при
.
....... ▲
Пример 1:
,
и здесь знак эквивалентности означает,
что ряды и интегралы, стоящие по разные
стороны этого знака сходятся или
расходятся одновременно. Тогда ряд 
сходится при р >1
и расходится при р
1.
Пример 2: Дзета-функция Римана ζ(z).
Def:
;
.
Если 
,
а
ряд 
сходится или расходится одновременно
с интегралом 
.
т.
е. ряд 
сходится, если Re z
> 1 и расходится при
Re z 
1.