Раздел 10. Кратные интегралы. §. Начальные понятия и определения
Def.Пусть
,
,
.
Множество
называется замкнутым промежутком или
замкнутым брусом в
.
Множество
называется открытым промежутком
или
открытым брусом в
.
Def.Мерой промежутков
и
называется величина:
( Точнее
).
Def.Если
такое, что
то промежуток
называется вырожденным и
.
Свойства меры промежутка:
а).
Положительность:
,
причем
тогда и только тогда, когда
– вырожден.
б).
Положительная однородность:
.
в). Аддитивность:
*
для
таких, что
;
*
для 
и
.
г).
Монотонность меры:
.
Def.Диаметром бруса (промежутка) называется величина:
Отметим,
что
и
– это не одно и тоже. Например, если
–
вырожден, то
,a
(вообще говоря).
При
этом: *
;
*
;*
.
Def.Совокупность
подпромежутков промежутка
называется разбиением промежутка
,
если: *
;
*
;
*
;
*
;
*
.
Величина
называется параметром разбиенияP(при этом
).
Def.Разбиение
называется измельчением разбиения
,
если все элементы разбиения
получены разбиением элементов
разбиения
.
Обозначается:
.
Читается:
мельче
или
крупнее
.
Для отношения “ крупнее – мельче” справедливо:
*. транзитивность
–
;
*.
;
*.
;
*.
|
.
§. Определение кратного интеграла
Пусть
– брус (промежуток) в
,
– разбиение промежуткаI.
На каждом из промежутков разбиения
отметим точку
.
Получим
разбиение с отмеченными точками для
.
Величина
называется интегральной суммой Римана
для функцииf (x)
на промежуткеI по разбиению с отмеченными точками
.
Def:
=
=
.
Обозначая
– множество функций интегрируемых
на брусеI запишем:
Def:
ε
> 0
δ>0
<
.
Если
для функции f(x)
наIи разбиения
– обозначить через
– наибольшее и наименьшее значение
функцииf(x)
наIk
то величины
=
и
=
называются нижней и верхней суммами
Дарбу.
§. Критерий Дарбу существования кратного интеграла.
Т0.
Чтобы функция
была интегрируема на брусе
(т.е.
)
необходимо и достаточно, чтобы
.
Δ▲.
Определено интегрирование функции по брусу в евклидовом пространстве. А как функцию проинтегрировать по произвольному ограниченному множеству из евклидового пространства?
Определим
интеграл от функции f
по множеству
.
Def:Пусть
и
– ограничено, т.е.
.
Функцию
назовём характеристической функцией
множестваM.
Тогда:
≡
.
Определение
интеграла по множеству не зависит
от того, какой брус, содержащий Мвыбран, т.е.
.
Это обозначает, что определение интеграла по множеству корректно.
Необходимое условие интегрируемости. Чтобы функцияf(x) наМбыла интегрируемой необходимо, чтобыf(x) была ограниченной наМ. Δ▲.
§. Свойства кратных интегралов.
1.Линейность: МножествоRMфункций интегрируемых на множествеМ –линейное
пространство,
а
–
линейный функционал.
.
2.Условие нормировки:
.
Другая форма записи
по сути дела определяет меру произвольного
множества из евклидового пространства.
3.Если интеграл по множеству Лебеговой меры ноль существует, то он
равен нулю.
Примечание:МножествоМназывается множеством Лебеговой меры ноль,
если
такие, что
и
.
4.а.
;б. 
;
в.если
и
–
отделена от нуля наМ, то
5.
иf=gп.в. (почти всюду) наМ, то
.
6.Аддитивность: Если
и
то
,
В
общем случае:
.
Δ.
Следует из равенства:
▲
7.Монотонность:
и
то
.
8.Интегрирование неравенств: если
и
то
.
9.Пусть
.
Для того чтобы
,
необходимо и достаточно чтобы
существовала внутренняя точка множестваМ, в которойf
(x) > 0 и непрерывна.
10.Интегрируемость модуля интегрируемой
функции:
.
11.Теорема о среднем:
,
наМсохраняет знак и
,
то
.
Если
множество М– связно иf(x) – непрерывна на
то
такое, что
.
12.Для того чтобы интеграл от неотрицательной функции был равен 0
необходимо и достаточно, чтобы f(x) = 0 почти всюду наМ.
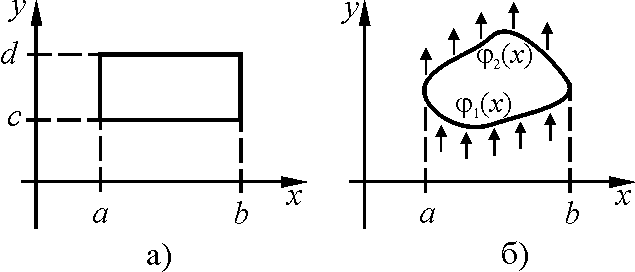
13.Теорема Фубини.Для двойного интеграла:
Пусть
область
– прямоугольник:
.
Тогда, при условии существования
внутренних однократных интегралов, для
нахождения двойного интеграла можно
перейти к повторному интегрированию
(см. рис. а):
,
или
.
Е
.
(*)
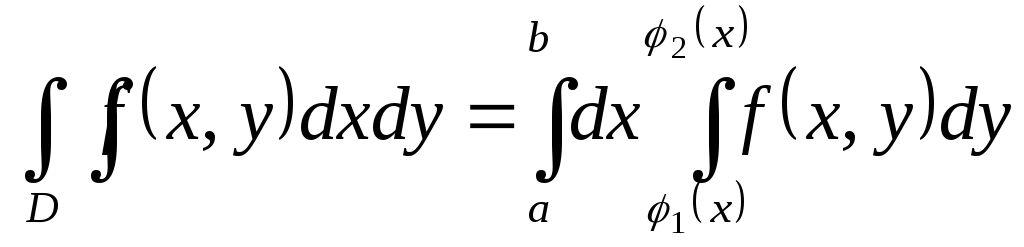Примечание: Внешние пределы интегрирования должны быть константами, внутренние пределы интегрирования могут зависеть от переменной, по которой интегрирование ещё предстоит.
Формула (*) может быть получена с использованием характеристической функции множества D.
Для многократного интеграла:
Пусть
и
некоторые подмножества евклидовых
пространств
и
.
Определим декартово произведение этих
множеств, являющееся подмножеством
евклидового пространства
:
.
Тогда
теорема Фубини для
имеет вид:
.
Теорема справедлива и для брусов XиY, и для более сложных конфигураций.
Примеры:
10.Вычислить
,
если граница области
задана уравнениями:
.
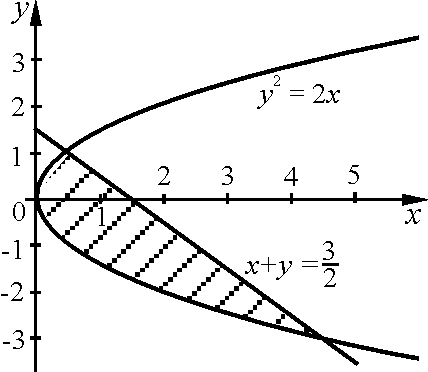
Находя точки пересечения кривых
определяющих границу области, получаем
две точки :
и
.
Тогда возможная расстановка пределов
интегрирования при переходе к повторным
интегралам дает:
а).
;
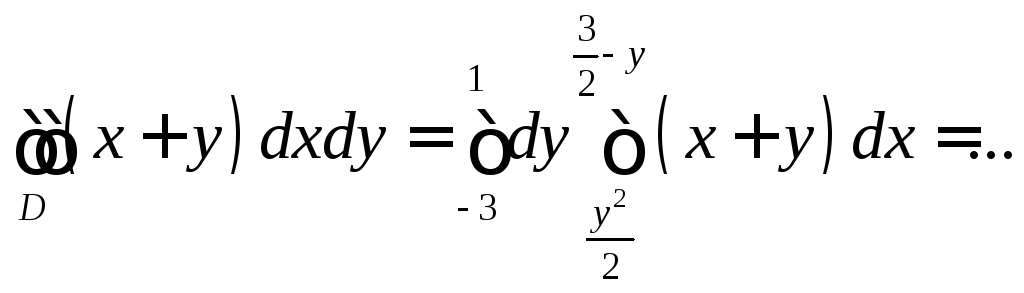б).
.
2
.
–
.
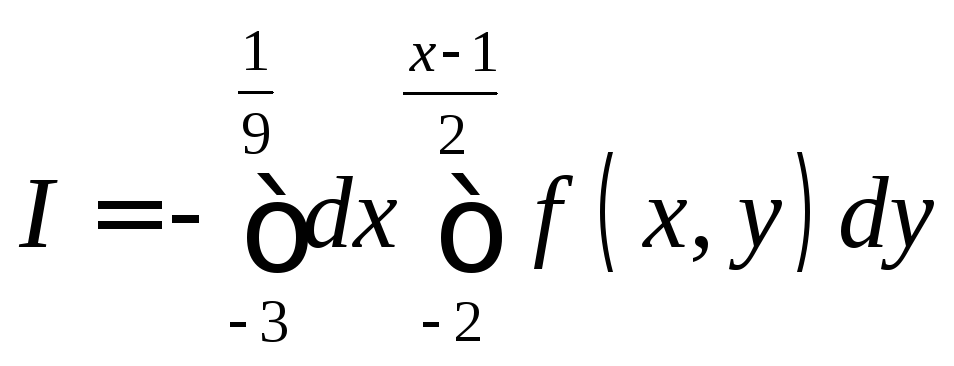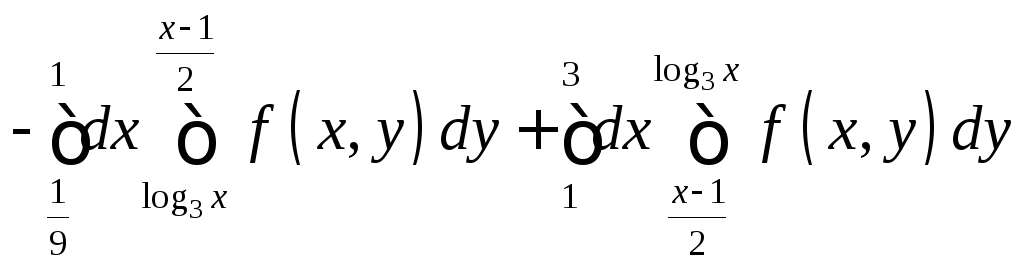Рецепт:При расстановке пределов интегрирования в двойном интеграле рекомендуется начинать с внешних пределов интегрирования .
3
,
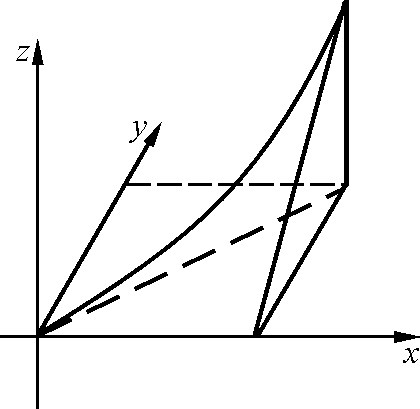
если
Переход к повторным
интегралам даёт:
.
При этом, в тройном интеграле расстановку пределов надо начинать с внутренних пределов интегрирования. Затем спроецировать область Vна плоскостьxOy
расставив пределы в области D– лежащей в плоскостиxOy.
40.Изменить порядок интегрирования в
повторном интеграле:
.
а).
;
б).
.