§. Задача о нахождении площади поверхности.

“Сапог Шварца”.

При рассмотрении длины кривой мы фактически определили длину кривой как предел длины вписанной в кривую ломанной, когда максимальная длина звена ломаной стремится к нулю.

Казалось бы, что при решении задачи о площади поверхности логично ее определить как предел площади вписанного многогранника. Однако следующий пример показывает, что такой подход здесь не срабатывает.

Р

ассмотрим прямой круговой цилиндр высотыНи с радиусом основанияR. Разобьем его наmцилиндров высоты.

К

аждую окружность разобьем наnчастей и впишем в них правильныеn-угольники. Причем точки деления вышележащих окружностей лежат над серединами дуг нижней окружности. Соединим отрезками соседние вершины смежных по вертикалиn-угольников. Так построенный многогранник, вписанный в цилиндр называется « сапогом Шварца». Вычислим площадь

« сапога Шварца». .

Тогда: . Устремим. Получим.

П

редел этого выражения зависит от отношенияи, следовательно, не существует.

§. Поверхностные интегралы 1^-го рода.

Пусть в Е₃задана поверхность : ;

, и на поверхности Sзадана функция.

Проводя в области координатные линиии, получим в областиразбиение. В каждом элементе разбиения отметим точку.

Разбиение с отмеченными точками индуцирует натакже разбиение с отмеченными точками. В каждый отмеченной точке построим касательную плоскость к поверхности. Заменим поверхность на чешуйчатую поверхность, состоящую из кусочков касательных плоскостей.

Рассмотрим: . Здесь– координаты отмеченной точки,– скалярный элемент площади. Если такой предел существует, то он называется поверхностным интегралом 1-го рода и обозначается.

.

Физический смысл поверхностного интеграла 1-го рода– масса поверхностиSс поверхностной плотностью.

Свойства:

1.Условие нормировки:. Это условие обозначает, что поверхностный интеграл 1-го рода от единицы численно равен площади поверхности.

2.Интеграл не зависит от стороны двухсторонней поверхности, по которой

идет интегрирование: .

3.О нахождении: 

 = .

Еще рассмотрим: .

= = ,

Здесь: ,,

.

Величина: называетсяпервой квадратичной формой поверхности.Эта квадратичная форма положительно определена. Ее матрица:и, следовательно, по критерию Сильвестра:.

Теперь отметим, что: и. Возведем оба соотношения в квадрат и сложим. Получим:.

Тогда : .

4..

.

Примерывычисления поверхностных интеграловрода:

1.Вычислить, где– часть поверхности параболоида, отсекаемая плоскостью.

Δ

. Запишем параметрическое уравнение заданной поверхности:

.

Находя вектор нормали к поверх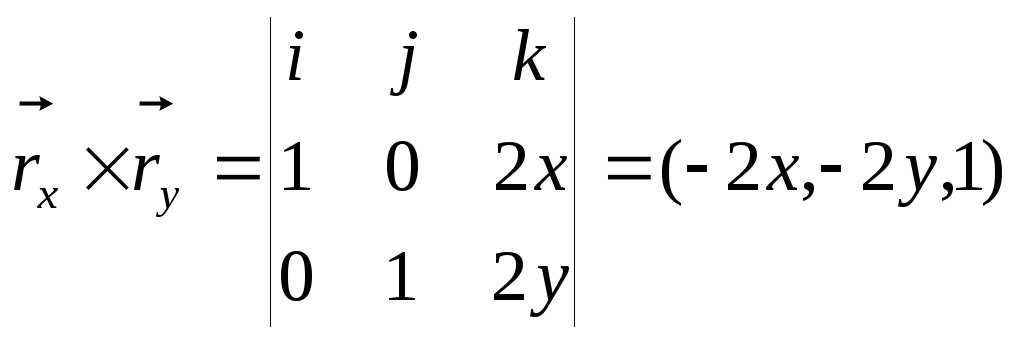ности , можем найти и элемент поверхности.

Параллельно получена формулы нахождения идля для функции заданной явно:

, .

Тогда, вычисляя исходный интеграл, получаем:

. Здесь – проекция поверхности интегрирования на плоскость, т.е. круг единичного радиуса. Переходя в полярную систему координат, вычисляем интеграл:

. ▲

2

.Вычислить, еслиS- граница тела:.

Δ. Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому .

Первый из этих интегралов – интеграл по кругу единичного радиуса и

.

Для вычисления второго из интегралов запишем параметрическое уравнение конуса в виде: и векторный и скалярный элементы площади поверхности:и. Тогда для искомого интеграла получаем:

= .▲

И, наконец, .

3.Вычислить, еслиS – полусфера ,.

Δ

. Параметрическое уравнение сферы радиусаа:

.

Тогда =

= 

 .

Тогда: =

= = 0.