§. Теорема Гаусса-Остроградского.

П

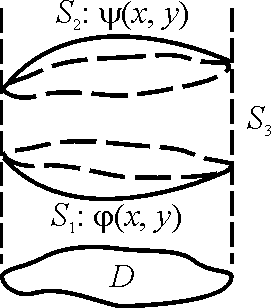
усть в замыканииобластизаданы функциинепрерывные навместе со своими производными. Тогда:

.

При этом, поверхность ориентирована наружу области.

∆. а) Рассмотрим :

.

Здесь учтено, что т.к.. Получено, что

.

б) и в) получаются аналогично:

, .

Складывая три полученные формулы, получим формулу Гаусса-Остроградского. ▲

Def:Величинадля векторного поляназывается дивергенцией векторного поля:,

и теперь формулу Гаусса-Остроградского можно записать так: .

*.Рассмотрим вточкуи– сферу радиусас центром в точке. Найдем:

.

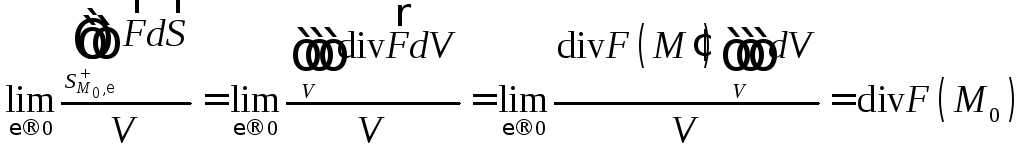(Здесь, по ходу преобразований была применена теорема о среднем).

Следовательно: ,

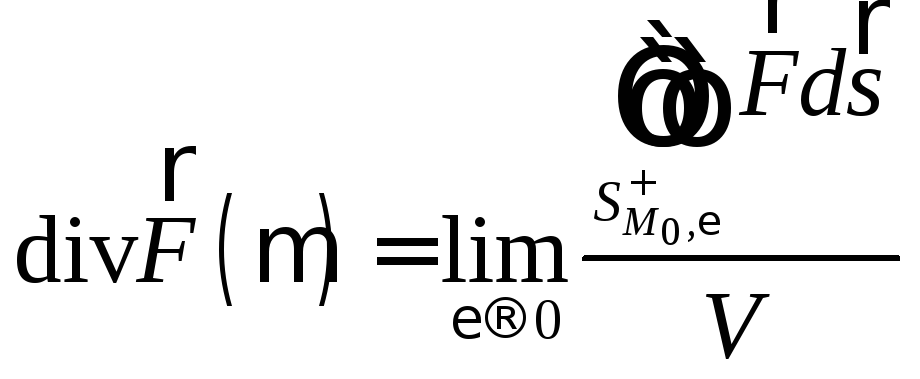т.е. дивергенция векторного поля есть мощность источника силовых линий поля, расположенного в точке. Это, инвариантное относительно системы координат, определение дивергенции.

И теорема Гаусса-Остроградского может быть сформулирована так, что будет ясен ее физический смысл:

Поток векторного поля через замкнутую поверхностьравен суммарной мощности источников векторного поля расположенных внутри области.

Дивергенция – еще одна, скалярная, характеристика векторного поля.

§. Теорема Стокса.

Пусть в заданы функции, непрерывные вместе со своими первыми производнымиПустьзамкнутый контур в, а–поверхность внатянутая на контур, причемодинаково взаимно ориентированы. Тогда:

= =

= .

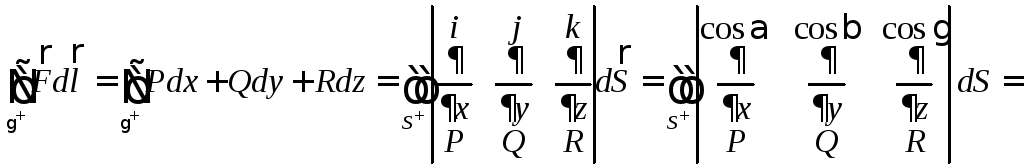
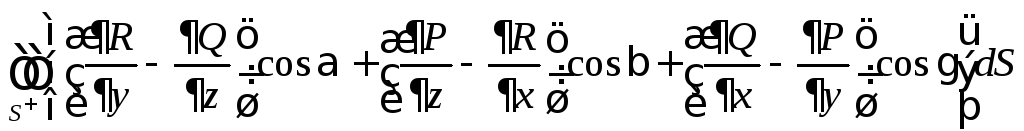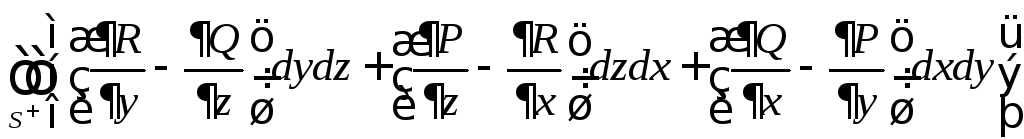∆. Интеграл по замкнутому контуру называется циркуляцией векторного поля.

а). Пусть .

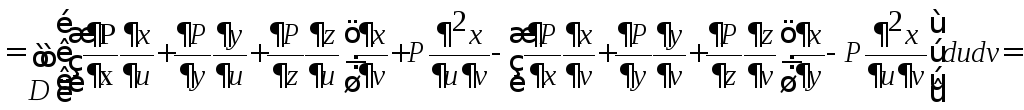
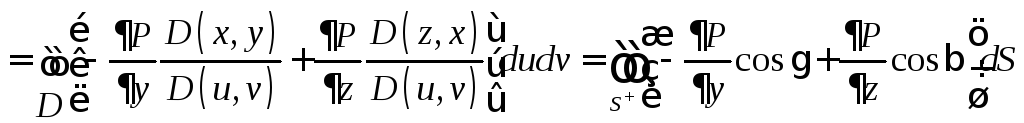
б), в) Аналогично:

, .

Суммируя полученные три формулы, получаем формулу Стокса. ▲.

D

ef:Вектор с координатаминазывается ротором векторного поля.,

и тогда формула Стокса запишется так: .

Рассмотрим ,и, найдем:

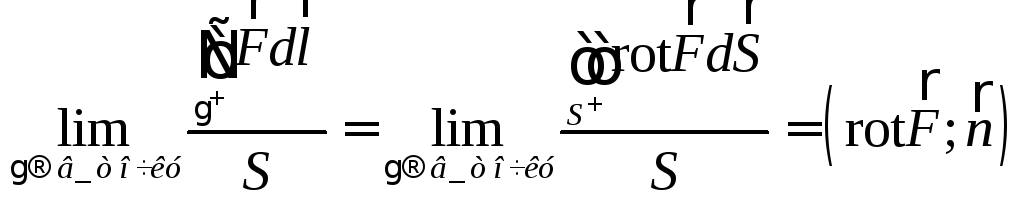следовательно:

Получили инвариантное относительно системы координат определение :

Проекция ротора векторного поля на вектор нормали к поверхности определяется пределом отношения циркуляциивдоль замкнутого контура к мере поверхности ограниченной данным контуром, когда контур стягивается в точку. И теорема Стокса:

Циркуляция векторного поля вдоль контураесть сумма циркуляций поляв точках расположенных на поверхности, краем которой является контур.

§. Задача о движении твердого тела.

Пусть твердое тело движется по закону: , где. Запишем

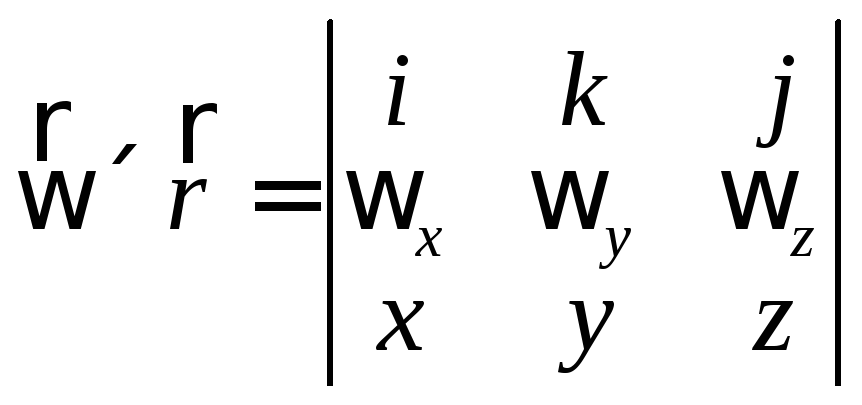, и тогда: ,,

.

П

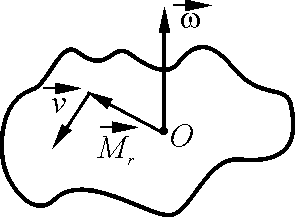
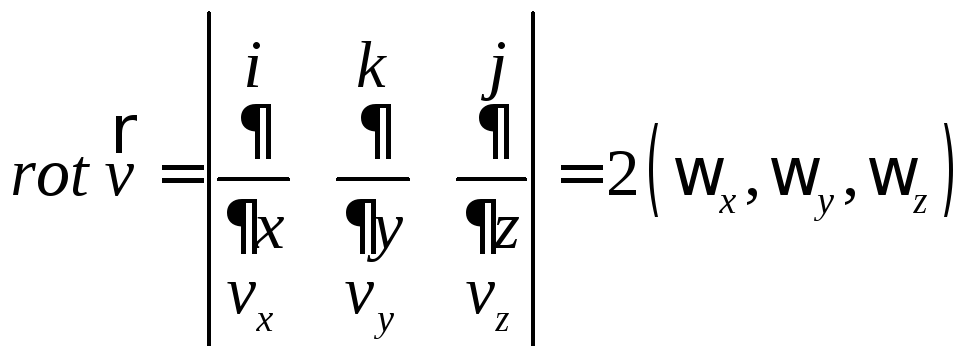олучаем тогда:т.е.. Этот пример объясняет термин «ротор поля» или «вихрь поля» или «вращение поля».

Примеры:

1. .

2. .

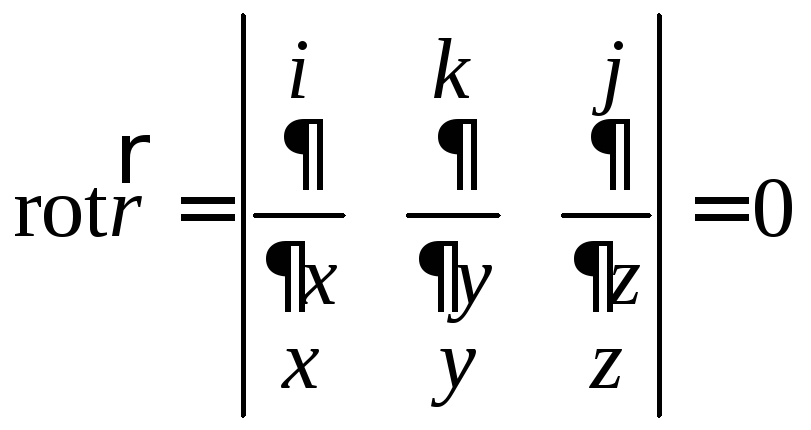3.

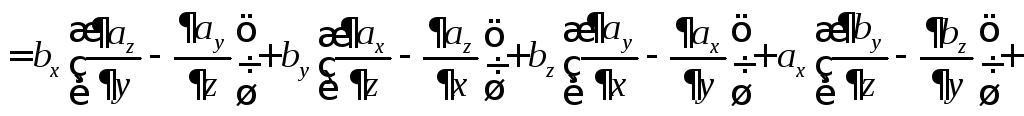
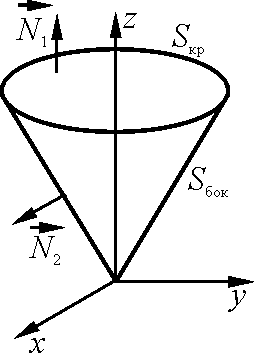
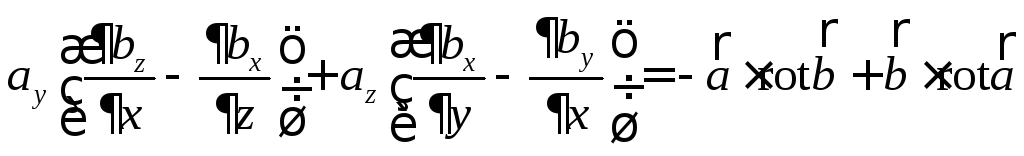
4. Вычислитьпо внешней стороне конусас крышкой.

Применяя формулу Гаусса – Остроградского, получаем:

§. ОПЕРАТОР ГАМИЛЬТОНА – ОПЕРАТОР «НАБЛА»

Введем векторно-дифференциальный оператор . Тогда легко

видеть, что: gradf(x,y,z) = ;div;rot.

Примеры вычислений с помощью оператора «набла»:

1.=

.

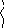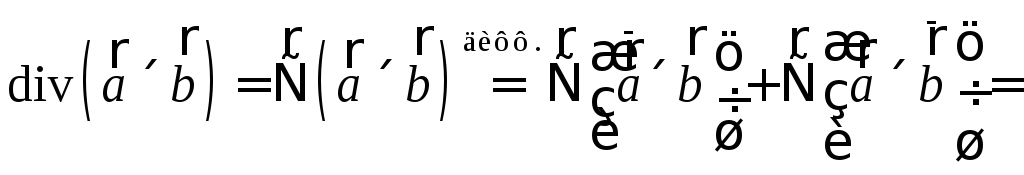
2. Найтиdivиrot, если– постоянный вектор,– радиус-вектор точки.

3. Найтиdivиrot.

4. Вычислить интеграл по замкнутой поверхностиS:,– постоянный вектор,– единичный вектор нормали кS, – радиус-вектор точки.

*** ДОПОЛНЕНИЕ 1

Элементы дифференциальной геометрии поверхностей

( почти другой подход )

Поверхность может быть задана параметрическим векторным уравнением:

или, что эквивалентно, системой параметрических уравнений в координатной форме:

.

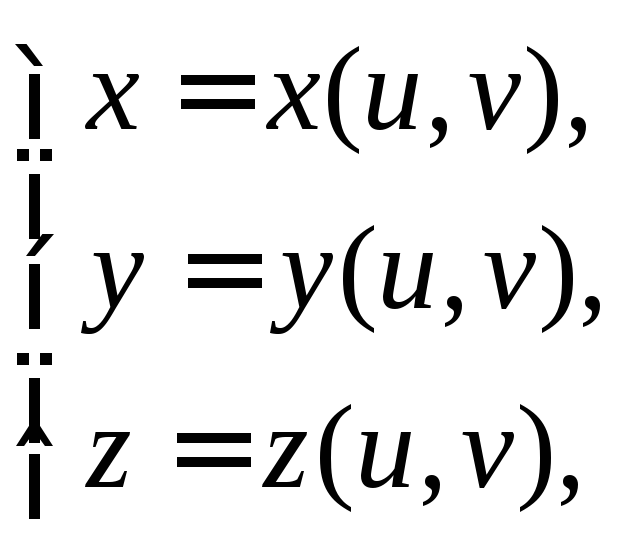
Переход от векторного уравнения к системе координатных уравнений производится разложением по базису, что в случае ортонормированного базиса можно осуществить последовательно умножая векторное уравнение скалярно на базисные векторы . Обратный переход осуществляется умножением координатных уравнений на соответствующие базисные векторы и суммированием полученных векторных равенств.

Точка принадлежащая параметрически заданной поверхности называется не особой, если касательные векторы к координатным линиям на поверхности не коллинеарны: в не особой точке В координатной форме это условие представимо в виде

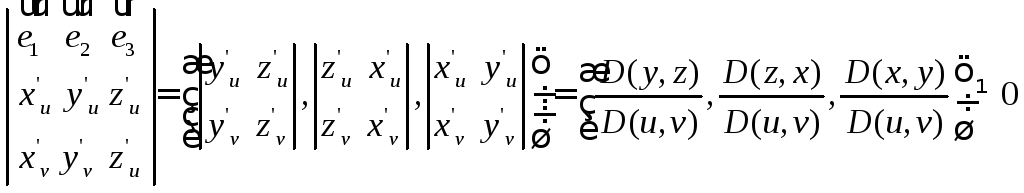
или, иными словами, .

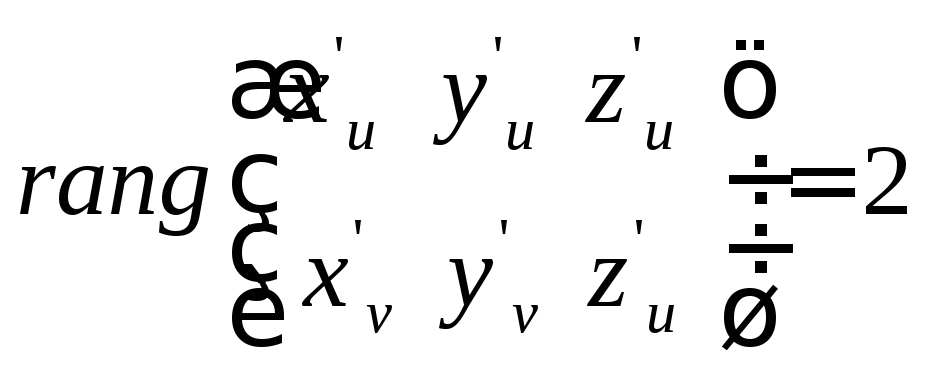Поверхность может быть задана явно, как график числовой функции двух числовых аргументов, скажем:

Явно заданная поверхность состоит из не особых точек.

Поверхность может быть задана неявно, как множество точек удовлетворяющих уравнению вида: .

Точка неявно заданной поверхности называется не особой ,если в этой точке вектор градиента ненулевой:.

или ,иными словами, .

Т.В окрестности не особой точки все три способа задания поверхности –параметрический, явный и неявный – эквивалентны.

∆ Представление явного уравнения в виде системы параметрических уравнений в координатной форме,

где первые два уравнения просто сообщают об отождествлении параметров с первыми двумя координатами, показывает, что явное задание это частный случай параметрического.

Запишем систему координатных параметрических уравнений , соответствующих явному заданию поверхности в векторной форме т.ч.

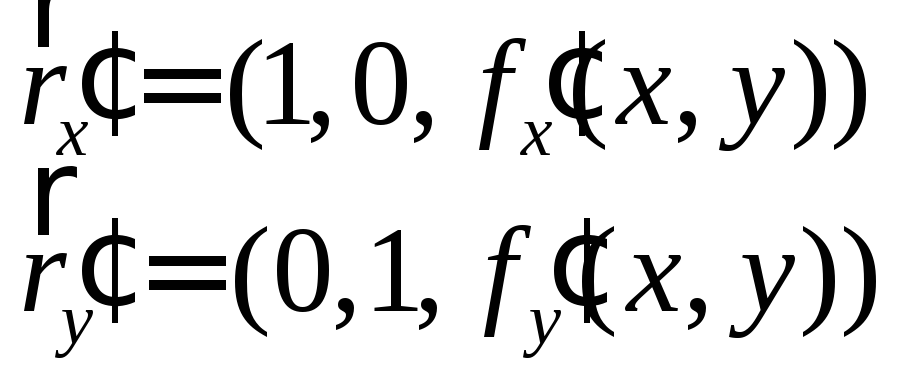. Следовательно .

Этим доказано, сделанное ранее утверждение о том, что явно заданная поверхность состоит из не особых точек.

Обратно, если поверхность задана параметрически, то предположим для определенности, что максимальный ранг матрицы , построенной из координат векторов ,касательных к координатным линиям на поверхности (условие не особости рассматриваемой точки) реализуется на первых двух столбцах:.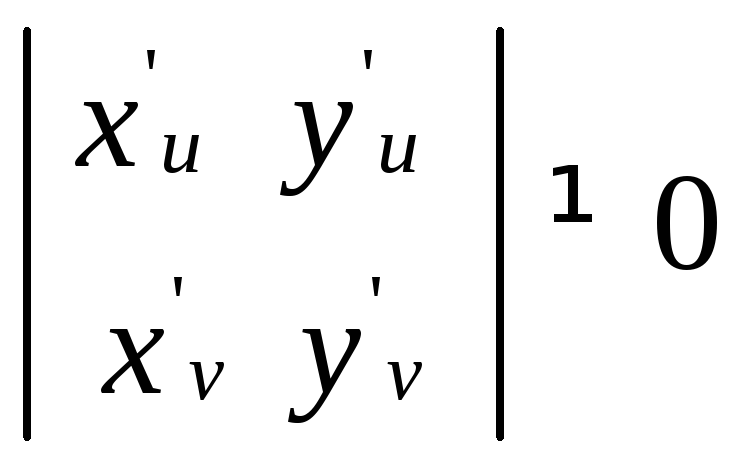

По теореме об обратной функции это позволяет разрешить первые два уравнения из системы координатных параметрических уравнений .

Заменим их эквивалентными , где правые части имеют тот же класс гладкости, что и правые части исходных уравнений.

Подстановка этих выражений в третье из системы координатных параметрических уравнений дает:где функцияимеет тот же класс гладкости, что и правые части исходных координатных параметрических уравнений.

Т.о. в окрестности не особой точки параметрический и явный способы задания поверхности действительно эквивалентны .

Уравнение , задающее поверхность явно, всегда можно записать в виде неявного уравнения, полагая.

Поскольку при этом , то заданная неявно поверхность, как и исходная, заданная явно, состоит из не особых точек.

Обратно, если поверхность задана неявно, то предположим, для определенности, что максимальный ранг матрицы ,построенной из координат вектора градиента образованного производными левой части уравнения поверхности по базисным векторам (условие не особости рассматриваемой точки) реализуется на последней координате.

По теореме об обратной функции это позволяет разрешить неявное уравнение, заменив его в некоторой окрестности рассматриваемой точки, эквивалентным явным уравнением того же класса гладкости. ▲

Элементарная поверхность – фигура, каждая точка которой имеет окрестность, такую что, часть фигуры, содержащаяся в этой окрестности, является элементарной поверхностью. Параметризация поверхности

где вектор-функция является, по меньшей мере, непрерывной функцией своих аргументов – вещественных параметров, которые пробегают двумерное множествоD, представляющее собой некоторую область (открытое связное множество) на плоскости, и называются гауссовыми координатами на поверхности.

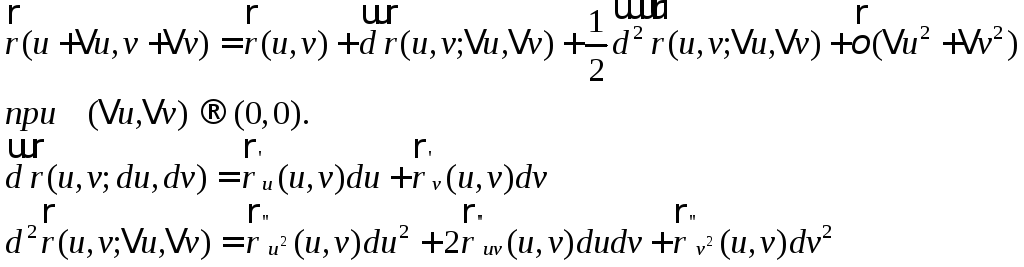
Записывая векторное параметрическое уравнение поверхности

В окрестности заданной не особой точки, отвечающей значениям параметров , с точностью до величин выше первого порядка малости по вектору приращений параметров, получим уравнение касательной плоскости

Соприкасающийся параболоид, параметризованный переменными с вершиной в рассматриваемой точке поверхности

Расстояние от точки на поверхности до параболоида до касательной плоскости более высокого порядка малости, чем квадрат расстояния от рассматриваемой точки поверхности до точки касания:

При величинаи:

Форма гладкой поверхности в окрестности не особой точки в первом приближении (с точностью до величин более высокого порядка, чем расстояние до рассматриваемой точки) воспроизводится касательной плоскостью , а во втором приближении (с точностью до величин выше, чем второго порядка по перпендикуляру к касательной плоскости относительно расстояния до рассматриваемой точки) касательным параболоидом. В зависимости от формы последнего , точки поверхности подразделяются на эллиптические, гиперболические, параболические и точки уплощения.

Проекция на касательную плоскость сечения касательного параболоида плоскостями параллельными касательной плоскости и удаленными от неё на расстояние 1/2 − индикатриса кривизны. В координатах уравнение индикатрисы

В точках уплощения индикатриса не существует; в параболических точках состоит из пары параллельных прямых.

Направление в рассматриваемой точке поверхности называется главным (асимптотическим), если оно совпадает с направлением оси (асимптоты) индикатрисы.

Последовательно

Вторая квадратичная форма поверхности− это проекция второго дифференциала радиуса-вектора текущей точки поверхности на нормаль к поверхности:

Квадратичные формы, первую ,положительно определенную, и вторуюможно одновременно привести к диагональному виду.

Для того, по матрицам иформ строим уравнение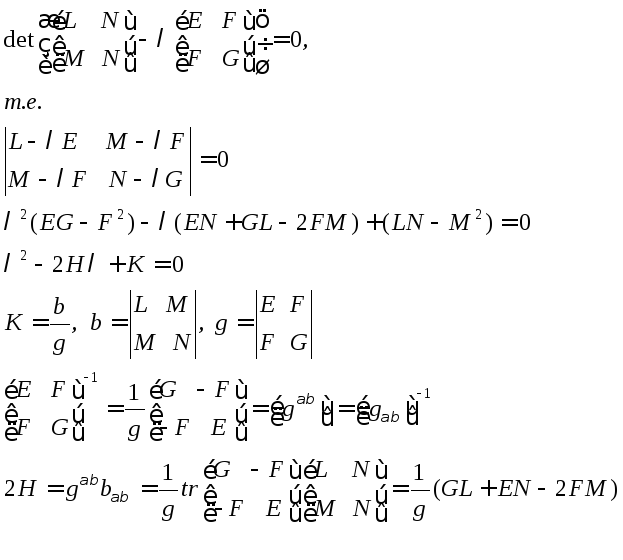

Теорема Виета

полная или гауссова кривизна –

средняя кривизна поверхности –

главные радиусы кривизны –

После приведения к диагональному виду

Поверхности с −поверхности постоянной кривизны; когдаэто сферы, когда, это псевдосферы − поверхности вращения, трактрисами

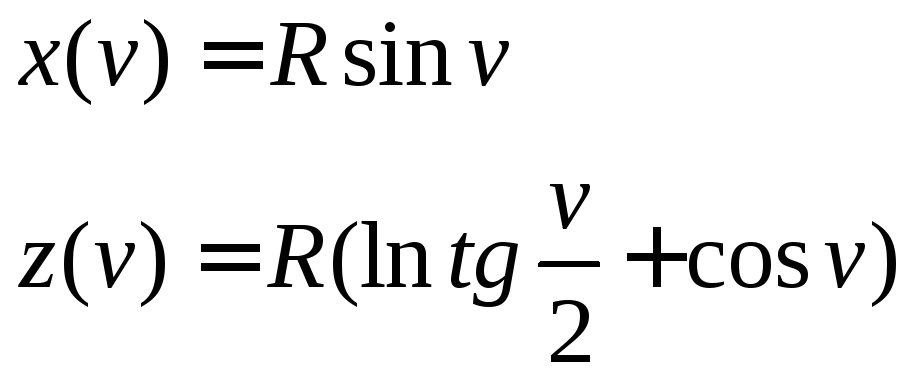
при вращении вокруг оси абсцисс. Для псевдосферы −псевдорадиус.

Трактрису описывает конец материального стержня длины ,движущегося под действием силы , направленной вдоль стержня, при условии, что конец свободен, но не отрывается о земли.

Если направить координатные оси в касательной плоскости по главным направлениям, то

(конечное условие могут потребовать изменения масштаба вдоль соответствующих осей), т.ч.где−главные кривизны , то обозначая

тоже не дает ничего.

Бонне: две квадратичные формы , из которых одна положительно определена, удовлетворяющих условиям Гаусса-Петерсона-Майнарди-Кодацци определяют поверхность ,для которой они являются первой и второй квадратичными формами соответственно, с точностью до положения в пространстве.

Тензор (кривизны) Римана

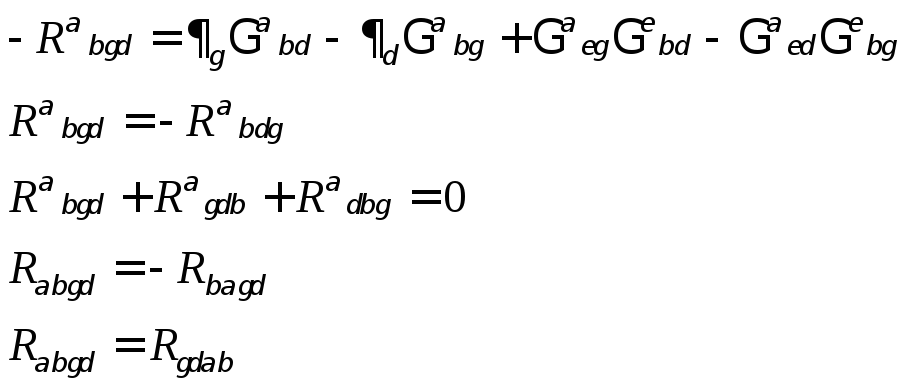
След тензора кривизны (Римана)−тензор Риччи

След тензора Риччи −скалярная кривизна

В тензоре кривизны два первых и два последних индекса ,если они расположены на одном уровне , не могут быть одинаковыми ,т.к. при их перестановке тензор меняет знак.

В случае двумерной поверхности единственный независимый компонент тензора кривизны

Для скалярной кривизны имеем

Нет двумерной гравитации, т.к. в двух измерениях (берем псевдо евклидову метрику)

ДОПОЛНЕНИЕ 2