§. Поведение функции, стоящей под знаком сходящегося интеграла, на бесконечности.

Замечание: Убывание подынтегральной функции ее стремление к нулю не является необходимым условием сходимости интеграла на бесконечности.

Пример. 1. Рассмотрим .

Особые точки: .

а). x = 0. – интеграл сходится  по признаку сравнения.

b). x = +. Сходится, вообще говоря (в.г.), условно по признаку Дирихле ибо – монотонно стремится к нулю, а функция имеет ограниченную первообразную.

c). x = 1. Тоже применим мажорантный признак: , т.е. сходится абсолютно при. Таким образом, исходный интеграл сходится в.г. условно для.

С

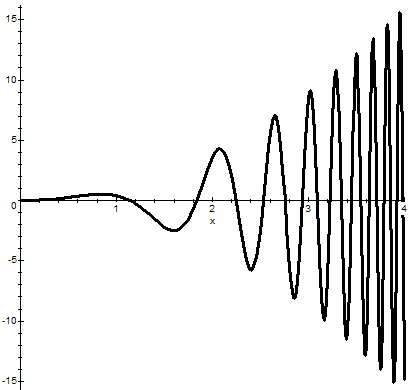
трого монотонная заменаприводит к выводу о том, что также сходится условно при , хотя его подынтегральная функция для неограниченна.

Происходит это за счет взаимного погашения площадей (см.Рис.).

Чтобы не создавалось впечатление, что сходимость появляется только за счет взаимного погашения площадей, приведем другой пример.

2. Построим функцию , которая равна нулю при всех положительных значениях аргумента, кроме промежутков, где она равна единице.

Тогда, интеграл есть площадь и . Таким образом, неотрицательная функция на бесконечности не стремится к нулю и, тем не менее, интеграл от нее сходится.

Можно на этой идее построить и f (x) которая будет неограниченной, а интеграл будет сходиться.

Таким образом, сходимость не означает, что f (x)  0 при x  .

Но...

Т. Если существует и конечен, то в случае сходимости интеграла на бесконечности

этот предел необходимо равен нулю.

Более того, если существует и конечен, то он также равен нулю.

§. Интегралы Фрулани.

Пусть функция таких, что и .

Рассмотрим интеграл: . Интегралы такого типа называются интегралами Фрулани. Для них:

= . Тогда:

= ===

= ==.

И, следовательно ==.

Выполняя предельный переход при и получаем:

.

Примеры:

1. .

2. 

§. Главное значение интеграла по Коши.

Рассматривается промежуток [a,b]. Пусть и при.

Тогда:

• Если оба предела существуют и конечны, то интеграл сходится.

• Если один из пределов существует и конечен, а другой равен бесконечности, то интеграл расходится.

• Если оба предела есть , то интеграл расходится, но…

Рассмотрим Полученное значение, если оно существует и конечно, называется главным значением интеграла (principal value). И говорят, что расходящийся интеграл сходится в смысле главного значения.

Пример:

.

Раздел 4. Численное интегрирование §. Формулы прямоугольников, трапеций и парабол (Симпсона)

З

а) б) в)

адача 1. Получить формулы приближенного вычисления:

а) Заменим f(x) для x[–, ] постоянной величиной по значению равной значению f(x) в средней точке. Тогда .

б) Заменим f(x) для x[–, ] многочленом первой степени, который на концах промежутка совпадает со значениями интегрируемой функции. Тогда .

в) Заменим f (x) для x[–, ] многочленом второй степени, совпадающим с интегрируемой функцией на концах и в середине промежутка интегрирования:

Ищем  .

Т.е. ;

И получаем: .

.

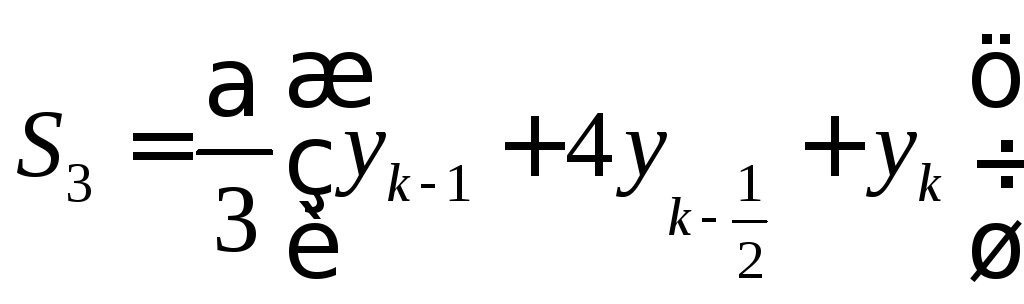Задача 2. Получить формулы для вычисления .

Р

азобьем промежуток интегрирования наn

равных частей, точками х₀, х₁, х₂, … , х_n. Обозначим у_k = f(x_k), k = 0, 1, 2, …, n; . Error: Reference source not foundНа каждом отдельном промежутке воспользуемся полученными выше формулами для S₁, S₂, S₃ и просуммируем по всем промежуткам. Получим:

;

;

.

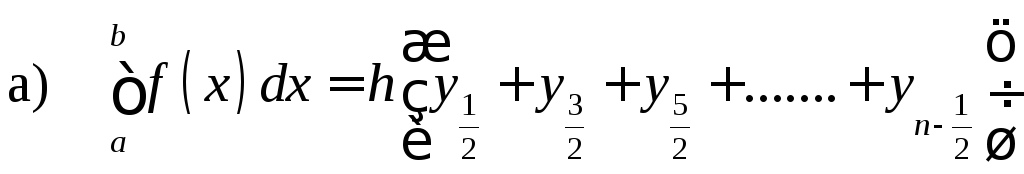Полученные формулы носят название формул:

а) прямоугольников; б) трапеций; в) парабол (Симпсона).

Эти формулы, естественно, являются приближенными и, возникает вопрос: каким должно быть выбрано n, чтобы обеспечить необходимую точность вычисленного значения интеграла?