
Высшая математика Часть 2
.pdf
34
35
ДОКАЗАТЕЛЬСТВО:
Вычислим смешанное произведение векторов a −b , b −c и c − a :
(a −b)(b −c)(c −a) =(ab −bb −ac +bc)(c −a) =,
=abc − bbc − acc + bcc − aba + bba + aca −bca =
=abc −bca = abc −abc = 0, это означает, что векторы компланарны.
Докажите тождество (a +c)b(a +b)= −abc .
ДОКАЗАТЕЛЬСТВО:
(a + c)b(a +b)= ((a + c), b,a )=.
=(a, b, a )+(c, b,a )= −abc
Даны векторы a1 ={1, −1,3}, a2 ={−2, 2,1}, |
|
||||||||||||||
a3 ={3, −2,5}. |
|
|
|
|
|
|
|
|
|
||||||
а) вычислите объем параллелепипеда, построенного |
|
||||||||||||||
на этих векторах; |
|
|
|
|
|
|
|
|
|||||||
б) вычислите объем тетраэдра, построенного на этих |
|
||||||||||||||
векторах; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) определите, будут ли векторы a1 , a2 , a3 компла- |
|
||||||||||||||
нарны; |
|
|
|
|
|
|
|
|
|
|
|
a1 , a2 , a3 базис |
|
||
г) определите, образует ли тройка |
7, |
||||||||||||||
в трехмерном пространстве; |
a3 правой. |
7 |
|||||||||||||
д) определите, будет ли тройка a1 a2 |
6 , |
||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
нет, |
||||||
1 |
−1 |
3 |
|
|
|
|
|
да, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
левая |
|||
а) Vпар = |
|
a1a2a3 |
|
= |
|
−2 2 |
1 |
= |
|
−7 |
|
= 7 , |
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
3 |
−2 |
5 |
|
|
|
|
|
|
б) V = |
1V |
= |
7 |
, |
|
|
|
|
|
|
|
||||
тетр |
6 пар |
6 |
|
|
|
|
|
|
|
|
|||||
в) векторы a1 , a2 , a3 некомпланарны, так как V ≠ 0 , |
|
||||||||||||||
г) тройка a1 , a2 , a3 |
образует базис в трехмерном про- |
|
|||||||||||||
странстве, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
д) тройка a1 , a2 , a3 – левая, так как a1a2 a3 = −7 < 0 . |
|
||||||||||||||
61
36
37
38
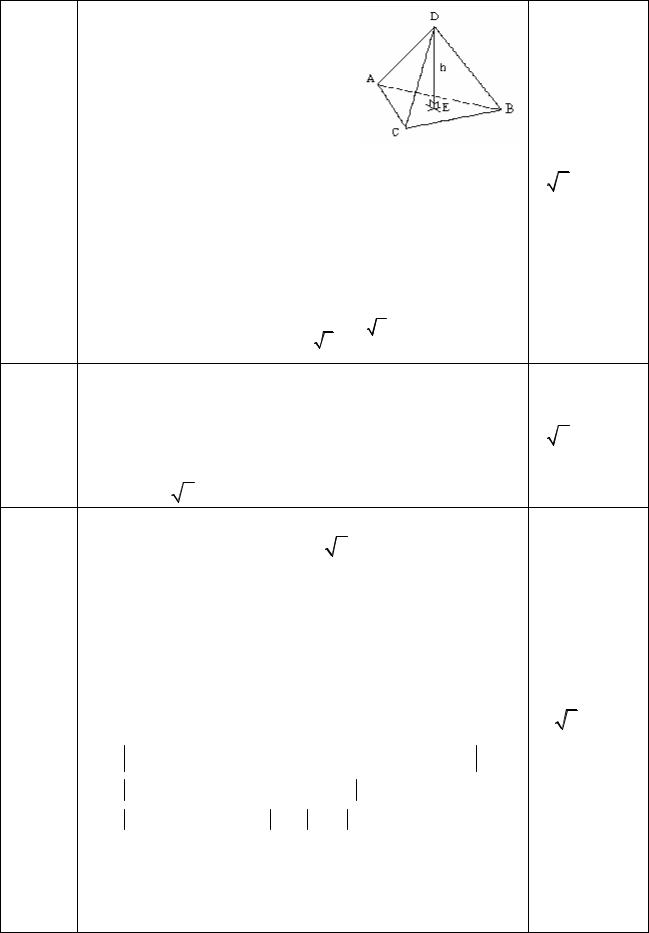
В тетраэдре с вершинами в |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
точках A(1,1,1), B(2, 0, 2), |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
C (2, 2, 2), D(3, 4, −3) |
вычис- |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
лите высоту |
|
|
DE |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
AB ={1, −1,1}, AC ={1,1,1}, |
|
|
|
|
|
|
|
3 |
2 |
|||||||||||||||||||||||
AD = |
{ |
2,3, − |
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
V = |
1 S |
|
h = |
1 |
|
1 |
|
AB, AC |
|
|
h ; |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
3 |
|
осн |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
V = |
1Vпар |
= 1 ( |
AB, AC |
|
, AD); |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h = |
|
( AB, AC , AD) |
|
|
|
= |
|
−12 |
|
= 3 |
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
AB, |
|
AC |
|
|
|
|
2 2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдите расстояние от плоскости, проходящей че- |
|
|
||||||||||||||||||||||||||||||
рез точки A(1,1,1) , B(2,0,2) , C(2,2,2) , до точки |
|
|
||||||||||||||||||||||||||||||
D(3,4,−3) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Построим тетраэдр ABCD и найдем его высоту |
|
|
||||||||||||||||||||||||||||||
| DE |=3 |
2 , как в предыдущей задаче. |
|
|
|
|
|
||||||||||||||||||||||||||
Длины базисных векторов e1 ,e2 ,e3 |
в пространстве |
|
|
|||||||||||||||||||||||||||||
равны соответственно 1, 2, |
2 , а углы между ними: |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
= |
120 |
o |
, |
|
|
= |
|
o |
|
|
|
o |
|
|
||||||||||||||
e1 |
,e2 |
|
|
|
e1 |
,e3 |
45 , |
|
e2 |
,e3 =135 |
|
|
. Вычис- |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
лите объем параллелепипеда, построенного на век- |
|
|
||||||||||||||||||||||||||||||
торах, имеющих в этом базисе координаты |
|
|
||||||||||||||||||||||||||||||
a ={−1,0,2}, b ={1,1,3}, c ={2,−1,1}. |
|
|
|
|
|
|||||||||||||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
V =| abc | = |
|
([−e1 + 2e3 ,e1 + e2 +3e3 ],2e1 −e2 + e3 ) |
|
= |
10 |
2 |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
=(−[e1 ,e2 ]−3[e1 ,e3 ]+ 2[e3 ,e1 ]+ 2[e3 ,e2 ]2e1 −e2 + e3 ) =
=−e1e2e3 +3e1e3e2 − 2e3e1e2 + 4e3e2e1 =
=e1e2e3( −1 −3 − 2 − 4 ) =10 e1e2e3 .
Осталось найти |e1e2e3 |. Выберем декартову систе-
му координат так, чтобы ось Ох была направлена по e1 , e2 лежал в плоскости oxy , тогда
e1 ={1,0,0},
62

39
40
e |
2 |
= |
{ |
} |
= |
{ |
−1, |
− |
} |
|
|
2 cos120o , 2sin120o , 0 |
|
3, 0 . |
Найдем e3 . Предположим, что он имеет декартовые координаты e3 =( x,y,z ). Воспользуемся известными углами между векторами e1 , e2 , e3 и их длинами:
( e , e |
) =1 |
|
|
2 cos 45o = |
2 |
|
2 |
=1; |
|
||||||||
|
|
|
|
|
|
||||||||||||
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( e1 ,e3 ) = e1xe3x +e1y e3 y +e1z e3z =1 x +0 y +0 z = x |
|||||||||||||||||
x =1; ( e |
2 |
, e ) = 2 |
2 cos135o |
= −2 . |
|
||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны, |
|
|
|
|
|
|
|
|
|
||||||||
( e2 ,e3 ) = −1 x − 3y +0 z = −x − 3y |
|
||||||||||||||||
−2 = −1x − 3y , |
|
|
|
|
|
|
|
|
|
||||||||
x =1 1 = 3y y = |
|
1 |
|
. |
|
|
|
||||||||||
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как | e |= |
2 = |
|
x2 + y2 + z2 |
z = ± 2 . Тогда |
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|||
| e1e2e3 |= |
|
|
|
|
|
|
|
= 2 , |
V =10 2 . |
||||||||
|
−1 − 3 |
0 |
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
1 |
|
± |
2 |
|
|
|
|
|
|
||
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Дайте алгебраическое доказательство того, что смешанное произведение трех компланарных векторов равно нулю.
ДОКАЗАТЕЛЬСТВО:
Даны три компланарных вектора a , b , c . Докажем,
что ( a,b ,c )= 0 .
Если a коллинеарен b a,b = 0 ( a,b ,c )= 0 .
Если a неколлинеарен b , то они образуют базис на плоскости, поэтому в силу компланарности a , b , c имеем c =αa + βb . Найдем
( a,b ,αa +βb)=α( a,b ,a)+β( a,b ,b)=
.
=α([a,a],b)+β( b,b ,a)=0
Докажите, что четыре точки A(1,2,−1), B(0,1,5), C (−1,2,1), D(2,1,3) лежат в одной плоскости.
63

ДОКАЗАТЕЛЬСТВО:
Точки A,B,C,D лежат в одной плоскости тогда и только тогда, когда векторы AB, AC,AD компла-
нарны, то есть AB AC AD = 0 . Вычислим
−1 −1 6
AB AC AD = −2 0 2 = −2 +12 −8 − 2 = 0 , 1 −1 4
что и требовалось доказать.
Дан параллелограмм ABCD . Докажите, что его площадь в два раза меньше площади параллелограмма A1B1C1D1 , противоположные стороны кото-
рого соответственно параллельны и равны диагоналям AC и BD исходного параллелограмма.
41ДОКАЗАТЕЛЬСТВО:
Если AB = a,AD = b , то. SABCD =| a,b |. Диагонали параллелограмма ABCD равны d1 = a +b и
d2 =b − a .
SA1B1C1D1 =| [a +b,b −a] |= 2 | [a,b] |= 2SABCD .
64

|
|
|
|
|
|
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
Задание |
|
|
|
Ответ |
||||
|
Составьте уравнение плоскости Р, проходящей через |
|
||||||||
|
точку M 0 (3,−2,−7) параллельно плоскости |
|
||||||||
|
P1 : 2x −3z +5 = 0 . |
|
||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|||||
|
В качестве нормального вектора |
|
||||||||
|
искомой плоскости Р можно вы- |
|
||||||||
1 |
брать нормальный вектор плоско- |
2x −3z − 27 = 0 |
||||||||
сти P1 |
n1 ={2, 0, |
−3} и уравнение |
|
|||||||
|
|
|||||||||
|
плоскости Р может быть записано в |
|
||||||||
|
виде уравнения плоскости, проходящей через точку |
|
||||||||
|
M 0 (3,−2,−7) с нормальным вектором n1 ={2, 0, −3}: |
|
||||||||
|
2(x −3) −3(z +7) = 0 . После приведения к виду общего |
|
||||||||
|
уравнения плоскости это уравнение принимает вид: |
|
||||||||
|
P : 2x −3z − 27 = 0 . |
|
||||||||
|
Составьте уравнение плоскости Р, проходящей через |
|
||||||||
|
точку M 0 (1,1,1) |
перпендикулярно прямой |
|
|||||||
|
L: |
x −1 |
= |
y + 2 |
= |
z +1 |
|
|
||
|
5 |
|
|
−1 |
|
|
||||
|
|
|
2 |
|
|
|
||||
|
РЕШЕНИЕ: |
|
|
|
|
|||||
|
В качестве нормального вектора |
|
||||||||
2 |
искомой плоскости выбираем на- |
5x + 2 y − z −6 = 0 |
||||||||
правляющий вектор прямой L, |
|
|||||||||
|
имеющий компоненты a ={5,2,−1} |
|
||||||||
|
из канонических уравнений дан- |
|
||||||||
|
ной прямой L. Уравнение плоскости, проходящей че- |
|
||||||||
|
рез точку M 0 (1,1,1) с нормальным вектором n ={5,2,−1} , |
|
||||||||
|
имеет вид: |
|
|
|
|
|||||
|
5(x −1) + 2( y −1) − (z −1) = 0 → 5x + 2 y − z −6 = 0 . |
|
||||||||
|
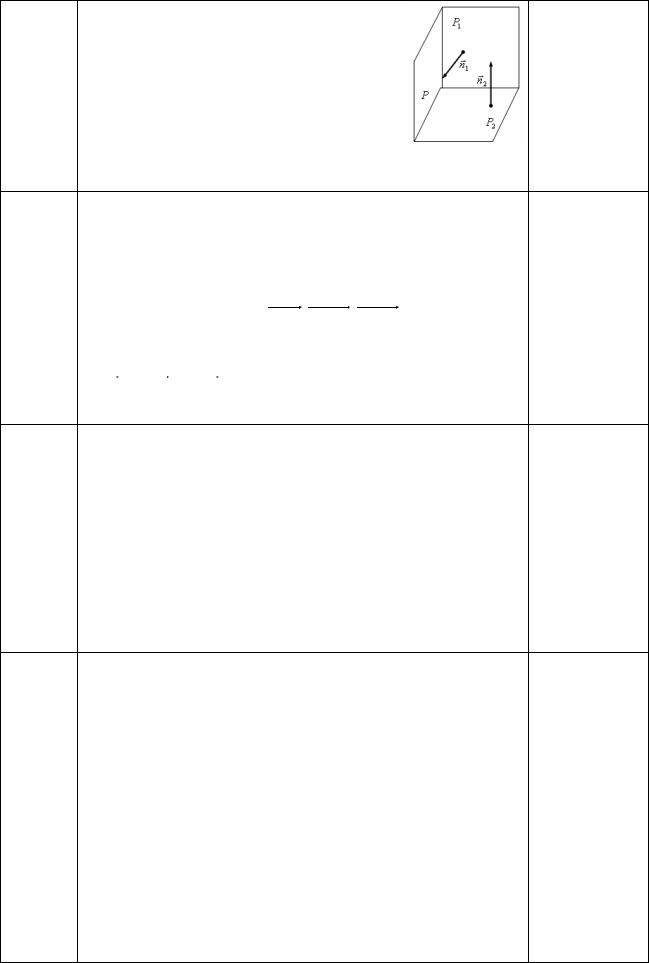
Составьте уравнение плоскости Р, проходящей через |
|
||||||||
|
точку M 0 (1,1,−1) перпендикулярно двум плоскостям |
|
||||||||
|
P1 : 2x − y +5z +3 = 0 и P2 : x +3y − z −7 = 0 . |
|
||||||||
3 |
РЕШЕНИЕ: |
|
={2, −1,5}, n2 ={1,3, −1} . |
2x − y − z − 2 = 0 |
||||||
По условию n1 |
|
|
||||||||
|
|
|
||||||||
|
Нормальный вектор искомой плоскости должен быть |
|
||||||||
|
перпендикулярен нормальным векторам плоскостей |
|
||||||||
|
P1 |
иP2 . |
|
|
|
|
||||
65
4
5
6
В качестве такого вектора можно выбрать их векторное произведение:
n = [n1 ×n2 ]= |
i |
j |
k |
|
2 |
−1 5 |
= −14i + 7 j + 7k. |
||
|
1 |
3 |
−1 |
|
|
|
|
|
|
Уравнение искомой плоскости имеет вид:
−14(x −1) + 7( y −1) + 7(z +1) = 0 2x − y − z − 2 = 0 .
Составьте уравнение плоскости Р , проходящей через три точки M1 (3,−1,2), M 2 (4,−1,−1), M 3 (2,0,2).
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Если M(x,y,z) - текущая координата плоскости, то |
|
|
|
|
||||||||||||||||||||||||||||||||
уравнение плоскости получается как следствие ком- |
3x +3y |
+ z |
−8 |
= 0 |
||||||||||||||||||||||||||||||||
планарности векторов MM1 , M1M 2 , M1M 3 , то есть ра- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
венства нулю их смешанного произведения: |
|
|
|
|
||||||||||||||||||||||||||||||||
MM1 M1M 2 M1M 3 = |
|
x −3 |
|
|
y +1 |
z − 2 |
|
= 0 3x +3y + z −8 = 0. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
1 |
|
0 |
|
−3 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|||||
Найдите отрезки, отсекаемые плоскостью |
|
|
|
|
||||||||||||||||||||||||||||||||
3x − 4 y − 24z +12 = 0 |
|
|
на координатных осях. |
|
|
|
|
|||||||||||||||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Приведем уравнение плоскости к виду уравнения |
|
|
|
|
||||||||||||||||||||||||||||||||
плоскости "в отрезках": |
|
|
|
|
|
|
|
|
|
|
|
-4; 3; 0,5 |
||||||||||||||||||||||||
|
3x |
|
|
|
− |
4 y |
|
− |
24z |
= |
1 |
|
x |
+ |
y |
+ |
|
z |
|
=1, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
−12 |
|
|
|
|
|
1/ |
|
2 |
|
|
|
|
|||||||||||||||||||
|
−12 |
|
|
|
−12 |
|
|
|
−4 3 |
|
|
|
|
|
|
|
||||||||||||||||||||
где |
|
|
|
|
a = −4, b = 3, c = |
|
1 |
|
|
− |
|
отрезки, отсекаемые |
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
плоскостью на осях ox, oy, oz соответственно. |
|
|
|
|
||||||||||||||||||||||||||||||||
Составьте уравнение плоскости Р, параллельной век- |
|
|
|
|
||||||||||||||||||||||||||||||||
тору p ={2,1,−1} и отсекающей на координатных осях |
|
|
|
|
||||||||||||||||||||||||||||||||
отрезки a = 3 |
и |
b = −2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Уравнение искомой плоскости "в отрезках" имеет вид: |
|
|
|
|
||||||||||||||||||||||||||||||||
|
x |
+ |
|
|
|
y |
+ |
z |
=1. Приведение его к общему виду |
|
|
|
|
|||||||||||||||||||||||
3 |
|
− 2 |
c |
2x −3y + z = 6 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 дает плоскость с нормальным |
|||||||||||||||||||||||||
− 2cx + |
3cy − 6z + 6c = |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
вектором n ={−2c,3c,−6}. Из условия перпендикулярно- |
|
|
|
|
||||||||||||||||||||||||||||||||
сти векторов n |
и |
|
|
p : (n p) = −4c + 3c + 6 = 0 |
|
|
|
|
||||||||||||||||||||||||||||
c = 6, |
n ={2,−3,1} , и уравнение плоскости принимает |
|
|
|
|
|||||||||||||||||||||||||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
+ |
y |
|
+ |
z |
|
=1 2x −3y + z = 6 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
3 |
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
66
7
8
9
Напишите уравнение плоскости, проходящей через точку M 0 (1,7,−5) и отсекающей от осей координат по-
ложительные и равные отрезки. РЕШЕНИЕ:
Уравнение плоскости, отсекающей от осей координат 2x −3y + z = 6 положительные и равные отрезки a , имеет вид:
|
x + y + z |
=1. Так как плоскость проходит через точ- |
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
куM 0 (1,7,−5) , |
a =1 + 7 −5 = 3 и уравнение |
|
|
|
|
|
|
|
||||||||||||||
плоскости принимает вид: x + y + z = 3 x + y + z −3 = 0 . |
|
|||||||||||||||||||||
Найдите угол между плоскостями P1 : x − y − 2z −6 = 0 |
|
|||||||||||||||||||||
и P2 : y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Один из двух смежных углов (острый) между плоско- |
|
|||||||||||||||||||||
стями равен углу между их нормальными векторами |
60° |
|||||||||||||||||||||
n1 ={1,−1,− 2} |
|
и n2 ={0,1,0} и находится из их ска- |
||||||||||||||||||||
лярного произведения: |
|
|
|
|
|
|
|
|||||||||||||||
cosϕ = |
|
(n1 n2 ) |
|
= |
|
1 0 −1 1− 2 0 |
|
= |
|
− |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
n1 |
|
|
|
n2 |
|
|
12 +12 +( 2)2 02 +12 +02 |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ϕ = 60°.
Найдите уравнение плоскости, проходящей через точки M (2,−1,4) и N (3,2,−1) перпендикулярно к плоскости
x + y + z −3 = 0.
РЕШЕНИЕ 1: |
|
|
|
|
||
Составим систему уравнений. Первое уравнение |
|
|||||
представляет уравнение плоскости, проходящей через |
|
|||||
точку М с нормальным вектором n ={A, B,C} . Второе – |
|
|||||
условие прохождения этой плоскости через точку N. |
|
|||||
Третье – условие перпендикулярности этой плоскости |
|
|||||
и заданной плоскости с нормальным вектором |
|
|||||
n1 ={1,1,1} . Получили однородную систему уравнений |
4x − 3y − z = 7 |
|||||
для определения А, В, С: |
|
|||||
A( x − 2 ) + B( y +1) +C( z − 4 ) = 0, |
|
|||||
|
A +3B −5C = 0, |
|
||||
|
|
|||||
|
A + B +C = 0. |
|
||||
|
|
|||||
Условие существования решения системы |
|
|||||
|
x − 2 |
y +1 |
z − 4 |
|
= 0 приводит к уравнению иско- |
|
|
|
|
||||
∆ = |
1 |
3 |
−5 |
|
|
|
|
1 |
1 |
1 |
|
|
|
мой плоскости: 4x −3y − z − 7 = 0. |
|
|||||
РЕШЕНИЕ 2. |
|
|
|
|
||
67

Вектор нормали ищем в виде n = MN × N ,
i j k
где N = {1,1,1}. Тогда n = 1 3 −5 =8i −6 j −2k .
1 1 1
Получаем уравнение плоскости
4(x −2)−3(y +1)−(z −4)= 0 .
Приведите уравнение плоскости 2x − y +2z +3 = 0 к нормальному виду и объясните смысл коэффициентов при неизвестных.
РЕШЕНИЕ:
Внормальном уравнении плоскости
xcosα+ycosβ+zcosγ −p =0.
|
коэффициенты представляют собой направляющие |
|
|
|||||||||||||||||||||
|
косинусы единичного вектора нормали к этой плоско- |
|
|
|||||||||||||||||||||
|
сти, р – расстояние от начала координат до плоскости. |
|
|
|||||||||||||||||||||
10 |
Общее уравнение плоскости Ax+By+Cz+D=0 с нор- |
2x − y + 2z = −3 |
||||||||||||||||||||||
мальным вектором n ={A,B,C} приводится к нор- |
|
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
мальному виду путем умножения на нормирующий |
|
|
|||||||||||||||||||||
|
множитель |
µ=± |
|
|
|
|
|
1 |
|
|
|
|
|
|
, знак которого противо- |
|
|
|||||||
|
2 |
2 |
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
A |
+B |
+C |
|
|
|
|
|
|
|
|||||||||
|
положен знаку D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
В данной задаче µ = −1 и уравнение плоскости при- |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
нимает следующий нормальный вид: |
|
|
|||||||||||||||||||||
|
− 2 x + |
1 y − |
2 z −1 = 0 |
или 2x − y +2z +3 = 0 . |
|
|
||||||||||||||||||
|
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите расстояние от заданной точки M 0 (−2,−4,3) до |
|
|
|||||||||||||||||||||
|
плоскости 2x − y + 2z +3 = 0 . |
|
|
|||||||||||||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Расстояние от точки M0 (x0 , y0 , z0 ) до плоскости с нор- |
|
|
|||||||||||||||||||||
|
мальным вектором {A,B,C} равняется |
|
|
|||||||||||||||||||||
11 |
|
|
d = |
|
δ |
|
= |
|
|
Ax0 +By0 +Cz0 +D |
|
|
. |
3 |
|
|||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 +B2 +C2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Здесь δ = 2(−2) −(−4) + 2 3 +3 |
= −9 = −3 < 0 , то есть на- |
|
|
||||||||||||||||||||
|
|
|
− |
4 +1+4 |
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||
|
чало координат и точка M 0 находятся по одну сторо- |
|
|
|||||||||||||||||||||
|
ну от плоскости. Искомое расстояние равно |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d = |
|
δ |
|
|
= 3. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|||||||||||||||||||||
12 |
Составьте уравнение плоскости, которая делит попо- |
4x −5y +z −2 =0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|

|
|
|
||
|
лам двугранный угол, образованный двумя пересе- |
2x + y −3z +8 =0 |
||
|
кающимися плоскостями: P1 : x −3y + 2z −5 = 0 и |
|
||
|
P2 : 3x − 2 y − z + 3 = 0. |
|
|
|
|
РЕШЕНИЕ: |
|
|
|
|
n1 ={1, −3, 2} |
и n2 ={3, 2, −1}: |
|
|
|
Уравнение пучка плоскостей, проходящих через пря- |
|
||
|
мую их пересечения: |
|
||
|
α (x −3y +2z −5)+ β (3x −2 y − z +3)= 0 . |
|
||
|
Выберем из них две, имеющие нормальные векторы, |
|
||
|
параллельные n1 + n2 |
={4, −1,1} и n1 − n2 = {3, 2, −1} . |
|
|
|
1) α +3β = |
−3α + 2β = |
2α − β , откуда α = β , |
|
|
4 |
−1 |
1 |
|
|
положив α = β =1, получаем уравнение первой плос- |
|
||
|
кости в виде 4x −5y +z −2 =0; |
|
||
|
2) α +3β = |
−3α + 2β = |
2α − β , откуда α = −β , положив |
|
|
2 |
5 |
−3 |
|
|
α = −1, получаем уравнение первой плоскости в виде |
|
||
|
2x + y −3z +8 =0. |
|
|
|
|
|
|
2. Прямая |
|
Прямая L задана общими уравнениями
x + y − z = 0, L : 2x − y +2 = 0.
Напишите канонические уравнения этой прямой и её уравнения в виде проекций на координатные плоскости.
РЕШЕНИЕ: Решим задачу двумя способами. 1-й способ
Найдем произвольную точку, лежащую на прямой, предположив, что
13 x = 0, тогда из системы, задающей прямую двумя уравнениями плоскости, найдем, что y = 2 и z = 2. Точка M 0 (0,2,2) L . В качестве направляющего векто-
ра прямой можно выбрать вектор
он будет перпендикулярен как n1 ={1,1,−1}, так и i j k
n2 ={2,−1,0}: a = 1 |
1 |
−1 ={−1,−2,−3}, и канонические |
||||||||
2 |
−1 |
0 |
|
|
|
|
|
|
|
|
уравнения прямой принимают вид: |
x |
|
= |
y − 2 |
= |
z − 2 |
и |
|||
−1 |
− 2 |
−3 |
||||||||
|
|
|
|
|
|
|||||
могут быть записаны в виде проекций на координат-
x |
|
|
= |
y − 2 |
= |
||
− |
1 |
− 2 |
|||||
|
|
||||||
= |
|
z − 2 |
, |
|
|||
|
|
|
|||||
|
|
|
− 3 |
|
|
|
|
3x+2 |
= |
3y +2 = |
||||
1 |
|
|
||||
|
|
|
2 |
|||
= |
z |
, |
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
||
3x − z + 2 = 0, |
||||||
|
|
|
|
+ 2 = 0, |
||
2x − y |
||||||
|
− 2z − 2 = 0. |
|||||
3y |
||||||
69

14
15
3x − z + 2 = 0,
ные плоскости следующим образом: 2x − y + 2 = 0,
3y − 2z − 2 = 0.
2-й способ
Из общих уравнений прямой L , исключая y и x в системе, получим уравнения прямой в проекциях на плоскости XOZ и YOZ:
|
|
z |
|
|
2 |
|
|
|||
x = |
|
|
|
− |
|
|
, |
|||
3 |
|
3 |
||||||||
|
|
|
|
|
|
|||||
2z |
|
|
2 |
|
||||||
y = |
− |
. |
||||||||
3 |
|
|
||||||||
|
|
|
3 |
|
||||||
Из этих уравнений z = 3x + 2 |
и z = |
3y + 2 |
и канони- |
||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
ческие уравнения прямой можно записать в ви- |
|||||||||||||||
де |
3x + 2 |
= |
|
3y + 2 |
= |
|
z |
. |
|
|
|
||||
|
|
|
2 |
|
1 |
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Докажите параллельность прямых |
|
||||||||||||||
|
|
x + 2 |
|
|
|
y −1 |
|
|
z |
|
|
|
x + y − z = 0, |
|
|
L1 : |
= |
|
= |
|
|
и L2 : |
|
|
|
||||||
|
|
|
|
|
− y −5z −8 = 0. |
|
|||||||||
3 |
|
|
|
− 2 |
1 |
|
|
x |
|
||||||
РЕШЕНИЕ:
Направляющий вектор прямой L1 имеет вид:
a ={3,−2,1}. Направляющий вектор прямой L2 может
быть выбран в виде векторного произведения нормальных векторов двух пересекающихся плоскостей
n1 |
={1,1,−1} |
|
и |
n2 ={1,−1,−5} : |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= [n1 ×n2 ]= |
i |
|
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|||||
a2 |
1 |
1 |
−1 |
={−6,4,−2}. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
−1 |
−5 |
|
|
|
|
|
|
|
|
|
|
|
Прямые L1 |
|
и L2 параллельны, так как компоненты их |
|
||||||||||||||||||||
направляющих векторов пропорциональны: |
|
|
|||||||||||||||||||||
|
l1 |
= |
m1 |
= |
n1 |
= − |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
m2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
l2 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определите угол между прямыми |
|
|
|
|
|
||||||||||||||||||
|
L |
: x −3 = y + 2 |
= z |
и L |
2 |
: x + 2 |
= y −3 |
= z +5 . |
|
||||||||||||||
1 |
|
1 |
|
|
−1 |
2 |
|
|
1 |
|
1 |
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|||||||||
Угол между направляющими векторами прямых L1 и |
|||||||||||||||||||||||
|
L2 |
a1 ={1,−1, 2} и |
a2 ={1,1, 2} определяется из значе- |
3 |
|||||||||||||||||||
ния их скалярного произведения: |
|
|
|
|
|
|
|||||||||||||||||
cosϕ = |
|
|
|
l1l2 |
+ m1m2 + n1n2 |
= |
1 −1 + |
2 |
= |
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
2 |
|
|||||||||
|
|
|
|
l12 + m12 + n12 l22 + m22 + n22 |
|
|
|
|
|||||||||||||||
70
