
Высшая математика Часть 2
.pdf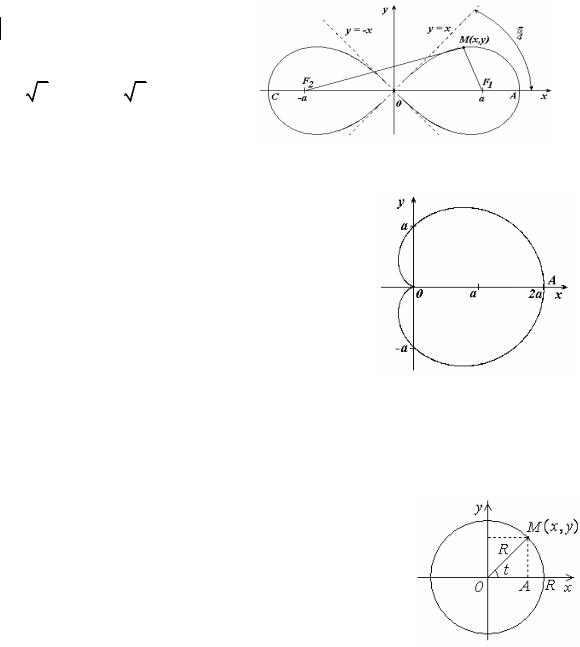
Лемниската Бернулли
Лемниската Бернулли - линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
ρ2 = 2a2 cos 2ϕ.
Покажем, что точка М лежит на кривой, если выполнено условие
|
|
|
|
|
F F |
|
|
2 |
|
|
|
||||||||
F1M |
|
F2M |
= |
|
|
1 2 |
|
|
. |
|
|
||||||||
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|||
Вершины кривой находятся в точках A(a 2,0); C(−a 2,0).
Площадь каждой петли S = a2.
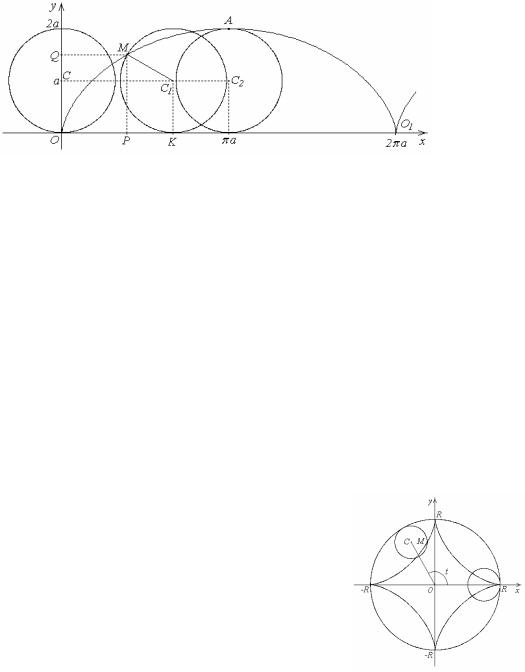
Кардиоида
В полярных координатах ρ = a(1 + cos ϕ), a > 0.
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды S = 3π2a2 , а длина
L = 8a.
3.6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
Окружность
Пусть M(x,y) - текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью OX 0 ≤ t < 2π. Из треугольника ОМА:
x = R cos t, |
- параметрические уравнения окружности. |
|
|
y = R sin t |
|
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
x2 + y2 = R2 (cos2 t +sin2 t) = R2 .
41
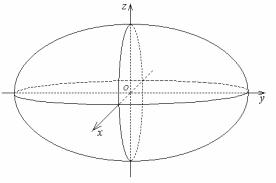
Циклоида
Циклоидой называется кривая, описываемая точкой круга, катящегося без скольжения по прямой линии.
Пусть ox - прямая, по которой катится круг радиусом а. Тогда МС=СК=а, где К - точка касания.
За параметр t примем угол поворота МС относительно СК: t = MCK - угол качения (в радианах). Так как качение окружности происходит без скольжения,
то ОК= MK =at. Из рисунка видно, что
x = OP = OK − PK = OK − MQ = at − asin t = a(t −sin t), y = PM = KC −QC = a − a cost = a(1 −cost).
Таким образом, параметрические уравнения циклоиды
x = a(t −sin t), |
где − ∞ < t < ∞. |
|
|
−cost), |
|
y = a(1 |
|
|
При 0 ≤t < 2π получаем первую арку циклоиды. Укажем, что длина дуги ОА1О1=8а, а площадь одной арки S = 3 πa2.
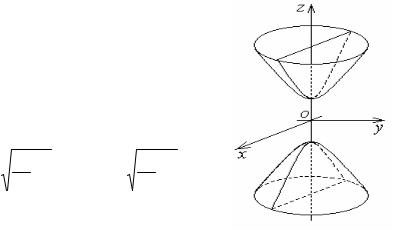
Астроида
Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R. Параметрические уравнения астроиды
x = Rcos3 t,
y = Rsin3 t,
где 0 ≤ t < 2π.
В декартовых координатах уравнение астроиды
x2/3+y2/3=R2/3.
Длина астроиды L = 6 R, а площадь, ограниченная астроидой, S = 3πR2/8.
42
4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Алгебраической поверхностью второго порядка называется поверх-
ность, уравнение которой в декартовой системе координат имеет вид:
Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+Gx+Hy+Iz+K=0,
где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае получаем алгебраическую поверхность первого порядка, т.е. плоскость).
В зависимости от значений коэффициентов возможны случаи, когда уравнение определяет вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).
Например, уравнение x2 + y2 + z 2 +1 = 0 не имеет решений и задает пустое множество, уравнение x2 + y2 + z 2 = 0 задает точку с координатами (0,0,0), уравнениеx2 − 2x +1 = 0 задает плоскость х = 1, уравнение x2 − y2 = 0 задает пару плоскостей х = у и х = −у.
Исследование формы поверхностей второго порядка по их каноническим уравнениям
Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями
x = const; y = const; z = const.
Эллипсоид
Эллипсоидом называется поверхность второго порядка с каноническим уравнением
|
x2 |
+ |
y2 |
+ |
z2 |
=1 |
. |
|
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
|
|
|||
Рассмотрим сечение эллипсоида плоскостью z = 0 . Линия пересечения эллипсоида и плоскости задается системой уравнений
|
2 |
|
y |
2 |
|
z |
2 |
|
|
x |
|
+ |
|
+ |
|
||
|
|
b2 |
c2 |
|||||
Γ: a2 |
|
|
||||||
|
|
|
z = 0 |
|
||||
|
|
|
|
|||||
|
|
2 |
|
y |
2 |
|
|
=1, |
|
x |
|
+ |
|
=1, |
|
|
|
b2 |
|||||
|
Γ: a2 |
|
|
||||
|
|
|
z = 0. |
||||
|
|
|
|||||
Г – эллипс с полуосями а и b в плоскости
z = 0 .
Рассмотрим сечение эллипсоида плоскостью z = h . Линия пересечения задается системой уравнений
|
2 |
|
y |
2 |
|
z |
2 |
|
|
2 |
|
y |
2 |
|
|
||
|
x |
|
+ |
|
+ |
|
=1, |
|
x |
|
+ |
|
|
=1, |
|||
Γ: a2 |
|
b2 |
|
c2 |
|
Γ: |
2 |
|
|
2 |
|
|
|||||
|
|
|
z = h |
|
|
a1 |
|
b1 |
|
||||||||
|
|
|
|
|
|
|
z = h, |
|
|||||||||
43

где a1 = a 1 |
− h2 |
; |
b1 = b |
1 |
− h2 . |
Таким образом, если 0 < h < c , |
то Г – эллипс с |
|||
полуосями |
c2 |
|
|
|
c2 |
в |
плоскости |
|
Если |
h = c , |
|
a1 |
< a; b1 |
< b |
z = h |
||||||
Г – точка с координатами |
(0,0, c). Если h > c , система решений не имеет, т.е. ис- |
|||||||||
следуемая поверхность не имеет общих точек с рассматриваемой плоскостью. Далее, так как переменная z содержится в уравнении во второй степени, плоскость z = 0 является плоскостью симметрии эллипсоида. Отсюда следует, что достаточно исследовать форму поверхности и построить ее часть в области z ≥ 0 , достроив затем остальную часть путем зеркального отражения найденно-
го фрагмента поверхности относительно координатной плоскости ОXY. Аналогично рассматриваются сечения поверхности плоскостями
x = const; y = const.
Эллипсоид - замкнутая овальная поверхность, имеющая три плоскости
симметрии: |
x = 0; y = 0; z = 0. |
||||||
|
|
|
Если |
a = b , каноническое уравнение эллипсоида принимает вид |
|||
|
x2 |
+ |
y2 |
+ |
z 2 |
|
=1. При этом линиями пересечения эллипсоида с плоскостями z = h , |
|
a2 |
a2 |
c2 |
||||
|
|
|
|
||||
где –с < h < c, являются окружности, центры которых лежат на оси OZ и, следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.
Если a = b = c = R , каноническое уравнение принимает вид x2 + y2 + z 2 = R2
и задает сферу с центром в начале координат и радиусом R.
Гиперболоиды
Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением
|
|
x2 |
+ |
y2 |
− |
z 2 |
|
=1 |
. |
||||||||
|
|
a2 |
|
|
c2 |
||||||||||||
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|||||
Линия пересечения |
|
гиперболоида и плоскости |
|||||||||||||||
z = 0 задается системой уравнений |
|
|
|||||||||||||||
|
|
|
|
2 |
|
y |
2 |
|
|
z |
2 |
|
|
|
|||
|
|
|
x |
|
+ |
|
|
− |
|
|
=1, |
||||||
|
|
|
|
|
|
|
c2 |
||||||||||
Γ: a2 |
|
b2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
z = 0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
иопределяет эллипс с полуосями а и b.
Всечении плоскостью z = h получаем эллипс
|
2 |
|
y |
2 |
|
|
|
|
x |
|
+ |
|
|
=1, |
|
|
|
|
|
|
|||
Γ: |
2 |
|
|
2 |
|
|
|
a1 |
|
b1 |
|
||||
|
|
z = h, |
|
||||
с большими, чем в предыдущем случае, полуосями
a = a |
1 + |
h2 |
и b = b |
1 + |
h2 |
. |
1 |
|
c2 |
1 |
|
c2 |
|
|
|
|
|
|
44
Сечение поверхности плоскостью |
x = 0 |
дает уравнение линии пересече- |
||||
ния в виде |
|
|
|
|
|
|
|
2 |
|
z |
2 |
|
|
|
y |
|
− |
|
=1, |
|
|
|
c2 |
||||
Γ: b2 |
|
|
||||
|
|
x = 0, |
||||
|
|
|||||
и представляет гиперболу, пересекающую ось OY.
Сечение плоскостью y = 0 задает гиперболу, пересекающую ось OX. Однополостный гиперболоид - поверхность, имеющая вид расширяю-
щейся трубки с тремя плоскостями симметрии x = 0; y = 0; z = 0.
Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность второго порядка с каноническим уравнением
|
x2 |
+ |
y2 |
− |
z 2 |
= −1 |
. |
|
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
|
|
|||
Линия пересечения гиперболоида и плоскости z = 0 задается системой уравнений
|
2 |
|
y |
2 |
|
|
|
x |
|
+ |
|
= −1, |
|
|
|
b |
|
|||
Γ : a2 |
|
2 |
|
|||
|
|
z = 0, |
||||
|
|
|||||
определяющей пустое множество.
В сечении плоскостью z = h имеем кривую
|
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ |
|
|
=1, |
где |
a1 = a |
h2 |
и b1 = b |
h2 |
||||||||||
|
|
b |
|
|
|||||||||||||||||
Γ : a |
2 |
|
2 |
|
|
c |
2 −1; |
c |
2 −1. |
||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
z = h, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если h > c , Г – эллипс с полуосями a1 , |
|
b1. |
|
|
|||||||||||||||||
Если h = с, Г – точка (0,0,c). |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для –с < h < c сечение – пустое множество. |
|||||||||||||||||||||
Сечение с плоскостью x = 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Γ : |
|
y |
|
− |
|
|
= −1, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дает гиперболу, пересекающую ось OZ.
Сечение плоскостью y = 0 также задает гиперболу, пересекающую ось OZ. Двуполостный гиперболоид - поверхность, имеющая вид двух беско-
нечно расширяющихся чаш с тремя плоскостями симметрии: x = 0; y = 0; z = 0.
Параболоиды
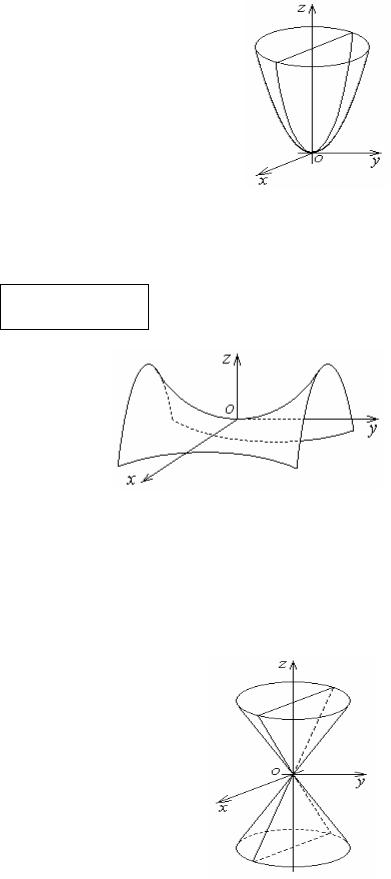
Эллиптический параболоид
Эллиптическим параболоидом называется поверхность с каноническим уравнением
45
|
|
|
x2 |
+ |
y2 |
= pz, |
p > 0. |
|
|
|
|
a2 |
b2 |
|
|||
|
|
|
|
|
|
|
||
Поверхность расположена в области z > 0 . Сечениями |
||||||||
в плоскостях |
z = h являются |
эллипсы, а в плоскостях |
||||||
x = h и y = h |
– параболы, в |
плоскости z = 0 – точка |
||||||
(0,0,0). |
|
|
|
|
|
|
|
|
Гиперболический параболоид
Гиперболическим параболоидом называется поверхность с каноническим уравнением
x2 |
− |
y2 |
= pz, p > 0. |
|
a2 |
b2 |
|||
|
|
Применение метода сечений приводит к тому, что в плоскостях z = h, где
h > 0 (h <0) , обнаруживаются гиперболы, а в плоскостях x = h и y = h > 0 – па-
раболы, в плоскости z = 0 – пересекающиеся прямые.
Конус
Коническая поверхность – множество прямых (образующих) пространства, соединяющих все точки некоторой линии (направляющей) с данной точкой (вершиной) пространства. Каноническое уравнение конуса второго порядка имеет вид:
|
x2 |
+ |
y2 |
− |
z 2 |
= 0 |
. |
|
a2 |
b2 |
c2 |
||||
|
|
|
|
|
Метод сечений позволяет составить представление о форме этой поверхности.
Осью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ. Поперечные сечения плоскостями z = h являются эллипсами, а в плоскостях XOZ и YOZ - пересекающиеся прямые, проходящие через начало координат, сечения плоскостями x = h и y = h – гиперболы, сечения плоскостя-
ми, не параллельными координатным, может дать параболу.
Цилиндры
Цилиндрическая поверхность – множество прямых (образующих) пространства, параллельных заданному направлению и проходящих через некоторую линию (направляющую).
46
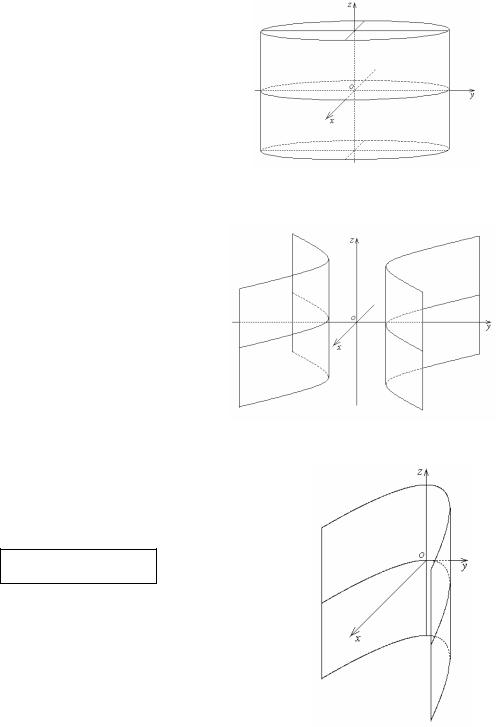
Эллиптический цилиндр
Эллиптический цилиндр задается ка-
ноническим уравнением
|
x2 |
+ |
y2 |
=1 |
. |
|
|
a2 |
b2 |
||||
|
|
|
|
|
||
Осью цилиндра является координатная ось OZ, поперечные сечения – эллипсы.
Гиперболический цилиндр
Гиперболический цилиндр задается каноническим уравнением
|
x2 |
− |
y2 |
=1 |
. |
|
a2 |
b2 |
|||
|
|
|
|
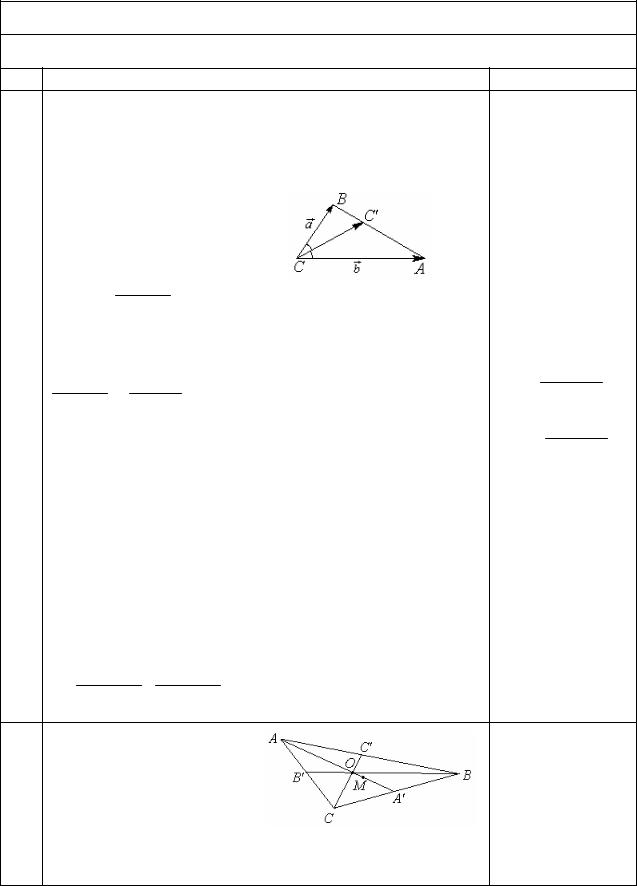
Параболический цилиндр
Параболический цилиндр задается канониче-
ским уравнением
y2 = 2 px, p > 0.
Заметим, что признаком рассмотренных цилиндрических поверхностей является отсутствие той переменной в каноническом уравнении, которой параллельна образующая.
47
5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1
ВЕКТОРНАЯ АЛГЕБРА
1. Векторы, базисы, координаты
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
Ответ |
|
|
|
||||||||||||||||||||||
|
В треугольнике |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
ABC разложите биссектрису CC′ по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
JJG |
|
G |
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
базису векторов a |
|
= CB и b |
= CA . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
G |
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Пусть a |
|
= CB , b = CA , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
C′ |
лежит на стороне AB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
CC |
′= aG |
+ α(b −aG), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
где α= |
|
|
|
|
|
BC′ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Воспользуемся свойством биссектрисы треугольника |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
CB |
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJG |
|
JJJG |
|
|
|
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и тем, что BA = BC′+ C′A . Отсюда JJJJG |
|
|
G |
|
|
|
|
|
|
|
|
|
G |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
JJJG |
|
|
= |
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
+ |
|
|
b |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CC′ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
G |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
b |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
α = |
|
|
|
|
|
|
|
BC′ |
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
a |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
BC |
|
′ |
|
+ |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
CA |
|
|
|
|
a |
|
+ |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C A |
|
|
1 + |
|
|
|
C A |
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC′ |
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
CC′= 1−α |
aG |
|
+αb = |
|
|
|
|
|
|
|
|
|
|
|
aG+ |
|
|
|
|
|
|
a |
|
|
|
|
|
|
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
+ |
|
G |
|
|
|
|
|
G |
|
+ |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
|
G |
|
|
|
|
|
|
|
|
G |
|
, |
|
|
|
G |
|
|
|
|
G |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
+ |
|
b |
|
|
|
|
|
|
|
+ |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Докажите, что точка пересечения медиан треугольника делит каждую
2 медиану в отношении
2 :1, считая от вершины.
РЕШЕНИЕ:
48
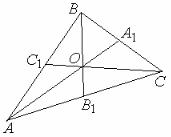
|
Пусть A′ – середина стороны BC , B′ |
– середина |
|
|||||||||||||||||||||||||||||||||||||||
|
стороны AC . Отложим на медиане BB′ |
расстояние |
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
BB ' |
|
от вершины и поставим точку O . Тогда |
|
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
|
|
||||
|
|
|
|
JJJG |
|
|
|
JJG |
|
|
|
|
|
|
|
|
JJG |
|
2 |
|
JJG |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
AO = AB |
+ |
|
|
BB′= AB + |
|
(BA + AB′)= |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 JJG |
|
+ |
1 JJJG |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
AB |
3 |
AC . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Отложим от вершины A по медиане AA′ |
расстояние |
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
AA' |
|
и поставим точку M . Найдем координаты |
|
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJG |
JJJG |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
вектора AM в базисе векторов AB и AC . |
JJJG |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
JJJG |
2 JJJG |
|
|
|
2 JJG |
|
1 JJJG |
|
|
|
2 JJG |
|
1 JJG |
|
||||||||||||||||||||||||
|
|
|
|
AM = |
|
AA′= |
|
|
|
AB + |
|
|
|
|
|
|
|
|
= |
|
|
AB |
+ (BA+ AC)= |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
BC |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
= |
1 JJG |
|
|
1 JJJG |
|
1 |
, |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
AB + |
|
|
|
AC |
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Но это координаты вектора AO . Таким образом, точ- |
|
||||||||||||||||||||||||||||||||||||||||
|
ка O и точка M совпадают, это − точка пересечения |
|
||||||||||||||||||||||||||||||||||||||||
|
медиан, и она делит медианы AA′ |
|
и BB′ в отноше- |
|
||||||||||||||||||||||||||||||||||||||
|
нии 2 :1, считая от вершины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
В треугольнике ABC через O обозначена точка пе- |
|
||||||||||||||||||||||||||||||||||||||||
|
ресечения медиан. Найдите сумму векторов |
|
|
|||||||||||||||||||||||||||||||||||||||
|
OA +OB +OC . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
AB = c , BC = a , AC = b, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||
b = a +c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Из рисунка по свойству медиан |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
получаем, что |
2 |
|
(A1 A + B1B +C1C)= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
OA +OB +OC = |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
b |
|
|
|
a |
|
c |
|
|
|
|
|
|
b |
|
|
|
a |
|
c |
|
|
1 |
(a +c −b)=0. |
|
||||||||||||||
|
= − |
|
+c −c − |
|
+ |
|
|
|
+a = − |
|
|
+ |
|
|
+ |
|
= |
|
|
|||||||||||||||||||||||
|
2 |
2 |
2 |
|
2 |
|
2 |
2 |
2 |
|
||||||||||||||||||||||||||||||||
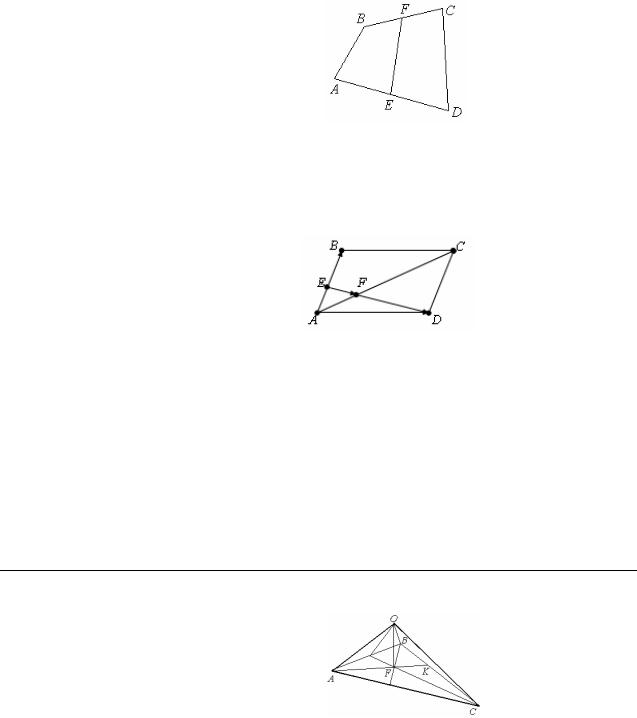
|
Точки E и F – середины сторон AD и BC четырех- |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
|
1 |
JJG |
JJGJ |
|
|||
|
угольника ABCD . Докажите, что EF = |
(AB |
+ DC). |
|
||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Выведите теорему о средней линии трапеции. |
|
|
||||||||||||||||||||||||||||||||||||||||
|
РЕШЕНИЕ: |
|
JJG |
|
|
|
JJG |
|
JJJG |
|
|
|
JJJG |
|
|
|
|
JJJG |
|
JJJG |
JJJG |
|
||||||||||||||||||||
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
EF |
= EA + AB + BF , EF |
= ED |
+ DC + CF , |
|
|||||||||||||||||||||||||||||||||
49
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
JJJG |
JJGJ |
JJG |
|
|
|
|
|
|
|
|
JJJG |
JJJG |
|
|
JJG |
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
BF = −CF , EA |
= −ED , |
EF = |
1 (AB + DC). |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Если ABCD - трапеция, сторо- |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
ны AB и CD параллельны, то- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
гда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
JJJG |
|
1 |
|
|
JJG |
JJJG |
|
|
|
|
|
|
|
|
1 |
JJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
EF |
= |
2 |
|
|
AB + DC |
|
|
= |
2 ( |
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
- свойство средней линии тра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
пеции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
На стороне AB и диагонали AC параллелограмма |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
ABCD взяты соответственно точки E и F так, что |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
AE = 1 AB и AF = |
|
1 |
|
|
|
|
|
AC . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
n |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Докажите, что точки E , |
F и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
D лежат на одной прямой и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
определите отношение отрез- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
ков EF иFD . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
ДОКАЗАТЕЛЬСТВО: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пусть AB = a , |
AD = b .Тогда a +b = AC . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
EF = AF − AE = |
|
|
1 |
|
|
|
|
(a +b) − |
1 |
a = − |
|
|
1 |
|
|
|
|
a + |
|
1 |
|
|
|
b . |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n + |
1 |
|
|
n(n +1) |
|
n +1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
FD = AD − AF = b − |
|
|
|
1 |
( a + b ) = − |
1 |
|
a + |
|
|
n |
|
b . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
n +1 |
n +1 |
n +1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Отсюда | EF |:| FD|= 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
EF || FD , то есть точки E , |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
F , D лежат на одной прямой. |
|
|
|
|
|
|
JJG |
|
|
JJG |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Задан тетраэдр OABC . В базисе из ребер OA , OB и |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OC найдите координаты векто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ра OF , где F – точка пересече- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ния медиан основания ABC . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
6 |
Воспользуемся правилом треугольни- |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
, |
1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|||||||||||||||||||||||||||||||
|
|
JJJG |
JJG |
JJJG |
|
|
JJG |
|
+ 2 |
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||
|
ка: OF = OA + AF = OA |
AK . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K – середина ребра CB ; точка F находится на рас- |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
стоянии |
2 длины медианы от вершины A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
JJG |
|
|
JJJG |
|
JJJG |
|
JJG |
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
JJJG |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
AK = AB |
+ BK |
= (AO |
+ OB) |
+ 1 BC |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50
