Algebra3

Легко видеть, что любой интервал является подрешеткой.

Предложение 2.20. Пусть A — модулярная решетка, a, b A. Тогда интервалы [a b, a] и [b, a b] изоморфны как ре- шетки.

Доказательство. Построим отображения

ϕ1 :[a b, a] → [b, a b], x 7→b x, ϕ2 :[b, a b] → [a b, a], y 7→a y.

Легко видеть, что действительно

a b ≤ x ≤ b b = b (a b) ≤ b x = ϕ1(x) ≤ b a, b ≤ y ≤ a b a b ≤ a y = ϕ2(y) ≤ a (a b) = a.

Используя условие модулярности, для любых x [a b, a] y [b, a b] получаем

(ϕ1 ◦ ϕ2)(x) = a (b x) = x (a b) = x, (ϕ2 ◦ ϕ1)(y) = b (a y) = y (a b) = y,

т. е. отображения ϕ1 и ϕ2 биективны. Пусть x1, x2 [a b, a]. Тогда

ϕ1(x1 x2) = b (x1 x2) = (b x1) (b x2) = ϕ1(x1) ϕ1(x2),

Необходимо также проверить, что отображение ϕ1 сохраняет операцию . Действительно,

ϕ2(ϕ1(x1) ϕ1(x2)) = a ((b x1) (b x2))

=a a (b x1) (b x2) = (a (b x1)) (a (b x2)

=(x1 (a b)) (x2 (a b)) = x1 x2 = ϕ2(ϕ1(x1 x2)).

Всилу инъективности ϕ2 имеем искомое равенство

Определение 2.21. Пусть A — решетка с наименьшим и наибольшим элементами 0 и 1. Нормальным рядом длины n (n N) в решетке A называется последовательность

0 = a0 < a1 < · · · < an = 1.

51

Композиционным рядом (или главным нормальным рядом)

называется такой нормальный ряд 0 = a0 < a1 < · · · < an = 1, что интервалы [ai, ai+1] простые для любого i = 0, . . . , n−1.

Естественно, не во всякой решетке (пусть даже содержащей 0 и 1) существует композиционный ряд. Но многие важные примеры решеток, например, Sub V для конечномерного линейного пространства V, Norm G для конечной группы G или Ideal R для полупростого артинова кольца R, обладают композиционными рядами.

Теорема 2.22 (о композиционных рядах). Пусть A — моду-

лярная решетка, в которой есть хоть один композиционный ряд. Тогда все композиционные ряды имеют одинаковую длину.

Доказательство. Достаточно показать, что если в модулярной решетке A есть композиционный ряд 0 = a0 < a1 <

· · · < an = 1, то все нормальные ряды этой решетки имеют длину, не превосходящую n.

Докажем это индукцией по n. При n = 1 по определению 2.21 интервал [a0, a1] = [0, 1] простой, т. е. A = {0, 1}; такая решетка не имеет нормальных рядов длины два.

Допустим, что для решеток, обладающих композиционным рядом длины n − 1, утверждение доказано. Предположим, в решетке A найдется нормальный ряд

0 = b0 < b1 < · · · < bn < bn+1 = 1

длины n + 1. Рассмотрим интервал A1 = [a1, 1] A — это решетка с композиционным рядом длины n − 1:

a1 < a2 < · · · < an = 1.

Рассмотрим последовательность элементов из A1

a1 = a1 b0 ≤ a1 b1 ≤ · · · ≤ a1 bn ≤ a1 bn+1 = 1.

В этой цепи обязательно найдется равенство a1 bi = a1 bi+1 для некоторого i {0, . . . , n}, так как иначе A1 содержит нормальный ряд длины n, что невозможно по предположению индукции.

52

Зафиксируем этот индекс i и рассмотрим

0 ≤ bi a1 ≤ bi+1 a1 ≤ a1.

Интервал [0, a1] простой, поэтому либо bi a1 = bi+1 a1, либо 0 = bi a1 и bi+1 a1 = a1. Первый случай невозможен: из равенств

bi a1 = bi+1 a1, bi a1 = bi+1 a1

иусловия модулярности вытекает bi = bi (bi a1) = bi (bi+1 a1)

= bi+1 (bi a1) = bi+1 (bi+1 a1) = bi+1,

что противоречит предположению bi < bi+1. Следовательно,

0 = bi a1, bi+1 a1 = a1,

т. е. a1 ≤ bi+1 и a1 bi+1 = bi+1. Из предложения 2.20 следует, что

[0, bi] = [bi a1, bi] [a1, bi a1] = [a1, bi+1 a1] = [a1, bi+1].

Интервал [0, bi] содержит нормальный ряд 0 = b0 < b1 <

· · · < bi, следовательно, в изоморфном интервале [a1, bi+1] существует нормальный ряд длины i, составленный из образов

b0, . . . bi:

a1 = c0 < c1 < · · · < ci = bi+1.

Но интервал [bi+1, 1] также содержит нормальный ряд bi+1 < bi+2 < · · · < bn+1 = 1. Тогда

a1 = c0 < c1 < · · · < ci = bi+1 < bi+2 < · · · < bn+1 = 1

— нормальный ряд длины n в интервале [a1, 1]. Существование такого ряда не допускается предположением индукции. Полученное противоречие доказывает, что нормального ряда длины n + 1 в решетке A не существует.

Замечание 2.23. Очевидно, что модулярная решетка A обладает композиционным рядом тогда и только тогда, когда в ней выполняется условие обрыва возрастающих и убывающих цепей (у.о.в.у.ц.): в любой последовательности

a1 ≤ a2 ≤ . . .

53

или

a1 ≥ a2 ≥ . . .

элементов из A лишь конечное число неравенств строгие.

Действительно, как показано в доказательстве теоремы 2.22 длина любой цепи не превосходит длины композиционного ряда. Обратно, если у.о.в.у.ц. выполняется, то по лемме Цорна существуют наибольший и наименьший элементы — это 1 и 0 соответственно. Далее, для любого a A, a 6= 1, множество [a, 1] \ {a} содержит минимальные элементы. Выберем какой-нибудь из них и обозначим его a′. Последовательность a0 = 0, ak+1 = a′k при ak 6= 1, k ≥ 0, является возрастающей цепью: 0 = a0 < a1 < . . . , которая обязана обрываться, т. е. an = 1 для некоторого n ≥ 0. При этом в силу выбора ak+1 = a′k все интервалы [ak, ak+1] простые.

Следствие 2.24. Для решетки A следующие условия экви- валентны:

(1)A модулярная;

(2)в любой подрешетке B A, обладающей компози- ционным рядом, все такие ряды имеют одинаковую длину.

Доказательство. (1) (2) Любая подрешетка модулярной решетки модулярна, поэтому к B применима тео-

рема 2.22.

(2) (1). Допустим, что A не модулярна. Тогда существуют x, y, z A такие, что x ≤ y, но

x′ = x (y z) < y (x z) = y′.

Обозначим a = y z, b = x z. Покажем, что множество {a, b, x′, y′, z} A является подрешеткой, изоморфной N5.

Действительно, по построению

a ≤ x′ < y′ ≤ b, a ≤ z ≤ b.

54

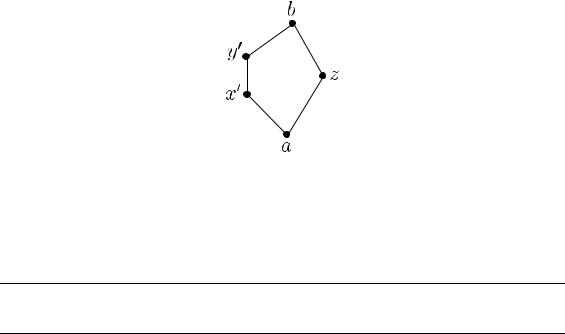
Все эти неравенства строгие:

a = z z ≤ y x′ = x z = b ≥ y′ x′ = y′, b = z z ≥ x y′ = y z = a ≤ x′ x′ = y′, b = y′ y ≥ x z y ≥ x, y ≥ z, y′ = x z

x′ = x (y z) = y ≥ y′ x′ = y′, x′ = a x ≤ y z x ≤ y, x ≤ z, x′ = y z

y′ = y (x z) = y z = x′.

Далее, x′ z = x (y z) z = x z = b, y′ z = y (x z) z = y z = a. Следовательно, элементы {a, b, x′, y′, z} образуют подрешетку в A, изоморфную N5.

В этой подрешетке, очевидно, есть два композиционных ряда разной длины.

Мы доказали, в частности, что любая не модулярная ре-

шетка, содержит подрешетку, изоморфную N5.

Упражнение. Покажите, что любая модулярная, но не дистрибутивная решетка, содержит подрешетку, изоморфную M5.

2.4. Прямые разложения.

Определение 2.25. Пусть A — решетка с наименьшим элементом 0. Отображение d : A → N{0} называется функцией размерности на A, если

(1)d(0) = 0;

(2)если [a, b] — простой интервал, то d(b) = d(a) + 1;

(3)d(a b) + d(a b) = d(a) + d(b) для любых a, b A.

Теорема 2.26. Пусть A — решетка с 0, в которой нет бес- конечных ограниченных линейно упорядоченных подмно- жеств. Тогда следующие условия эквивалентны:

55

(1)A модулярная;

(2)существует функция размерности на A.

Доказательство. Условие конечности ограниченных линейно упорядоченных подмножеств означает, что если B A, (B, ≤) линейно упорядоченное и существует a A такое, что B ≤ a, то |B| < ∞. В частности, любой интервал этой решетки удовлетворяет у.о.в.у.ц.

(1) (2) Если решетка A модулярная, то любой интервал удовлетворяет у.о.в.у.ц. и, следовательно, обладает композиционным рядом. Положим d(0) = 0, d(a) = l([0, a]), a A, — длина композиционного ряда этого интервала. Свойства 1 и 2 из определения 2.25 выполняются. Проверим свойство 3: объединяя композиционные ряды разных интервалов, получаем равенства

l([0, a b]) + l([a b, a]) = l([0, a]) = d(a), l([0, b]) + l([b, a b]) = l([0, a b]) = d(a b).

Но по предложению 2.20 [a b, a] [b, a b], поэтому длины их композиционных рядов равны. Следовательно,

d(a) − d(a b) = (d(a b) + l([a b, a])) − (d(b) − l([b, a b])) = d(a b) − d(b),

откуда следует искомое равенство.

(2) (1) Если решетка A не модулярная, то в ней есть подрешетка, изоморфная N5 (см. пример 2.17):

a < b, a c = b c, a c = b c.

Отсюда легко вывести d(a) = d(b), что невозможно при a < b.

Пусть A — решетка с наименьшим элементом 0. Говорят, что выражение a = x1 · · · xn, a, xi A, является прямым

-разложением, если

xi (x1 · · · xi−1 xi+1 · · · xn) = 0

для любого i = 1, . . . , n. Запись

a = x1 × · · · × xn

56

означает, что a = x1 · · · xn является прямым -разложением.

Предложение 2.27. Пусть A — модулярная решетка с композиционными рядами, a, xi A, a = x1 · · · xn. Тогда

a = x1 × · · · × xn d(a) = d(x1) + · · · + d(xn),

где d — функция размерности.

Доказательство. ( ) Это легко показать индукцией по n. Если n = 2, то

d(x1 x2) = d(x1) + d(x2) − d(x1 x2) = d(x1) + d(x2).

Если a = x1 × · · · × xn, то x1 · · · xn−1 = x1 × · · · × xn−1, так как xi (x1 · · · xi−1 xi+1 · · · xn−1) ≤ xi (x1 · · · xi−1 xi+1 · · · xn) = 0 для любого i = 1, . . . , n − 1. Тогда по предположению индукции

d(x1 · · · xn−1) = d(x1) + · · · + d(xn−1),

и искомое равенство вытекает из определения функции размерности.

( ) Обозначим x¯i = x1 · · · xi−1 xi+1 · · · xn. Если a = x1 · · · xn, то для любого i = 1, . . . , n

d(a) = d(xi) + d(¯xi) −d(xi x¯i) ≤ d(x1) + · · ·+ d(xn) −d(xi x¯i),

поскольку d(x y) ≤ d(x) + d(y) для любых x, y A. Равенство достигается только при d(xi x¯i) = 0, что означает xi x¯i = 0.

Элемент 0 6= a A называется неразложимым, если из a = x × y следует, что x = 0 или y = 0.

Из предложения 2.27 следует, что операция × в модулярной решетке с композиционными рядами коммутативна и ассоциативна в естественном смысле: если

a = x1 × · · · × xn, σ Sn,

то

a == xσ(1) × · · · × xσ(n);

если

xi = xi1 × · · · × ximi , i = 1, . . . , n,

57

то

a = x11 × · · · × x1m1 × · · · × xn1 × · · · × xnmn .

Лемма 2.28. Пусть A — модулярная решетка с компо- зиционными рядами. Тогда для любого 0 6= a A най- дутся неразложимые x1, . . . , xn A, n ≥ 1, такие, что a = x1 × · · · × xn.

Доказательство. Проведем индукцию по d(a). Если d(a) = 1, то a — неразложимый элемент (обратное неверно!). Если элемент a не является неразложимым, то a = a′ × a′′,

где 0 < d(a′), d(a′′) < d(a). По предположению индукции, для a′ и a′′ существуют такие неразложимые y1, . . . , ym, z1, . . . , zk,

что a′ = y1 × · · · × ym, a′′ = z1 × · · · × zk. Тогда a = y1 × · · · × ym × z1 × · · · × zk.

Из леммы 2.28 следует, что любое прямое -разложение 1 = a1 × · · · × an можно продолжить до разложения на неразложимые элементы, т. е. найти такие неразложимые

aij , i = 1, . . . , n, j = 1, . . . , mi, что ai = ai1 × · · · × aimi , 1 = a11 × · · · × anmn .

Оказывается, что в модулярной решетке с композиционными рядами прямое -разложение наибольшего элемента 1 на неразложимые элементы в определенном смысле единственно. Для этого нам потребуется дополнительное понятие.

Пусть A — решетка с 0 и 1. Два элемента a, b A называются прямо подобными, если существует такой z A, что 1 = a × z = b × z. Будем обозначать прямое подобие элементов a и b через a b.

Два прямых -разложения единицы

1 = a1 × · · · × an, 1 = b1 × · · · × bm

называются прямо подобными, если n = m и существует

подстановка σ Sn такая, что ai bσ(i), i = 1, . . . , n. Рассмотрим некоторые примеры прямого подобия.

В решетке Sub V всех подпространств конечномерного пространства V два элемента (подпространства) прямо подобны тогда и только тогда, когда их размерности совпадают.

58

Если в решетке Norm G всех нормальных подгрупп некоторой группы G два элемента (нормальных подгруппы) H1 и H2 прямо подобны, то они изоморфны. Действительно, если

G = H1 × H = H2 × H,

то

H1 G/H H2.

Именно, любой элемент x H1 единственным образом представляется в виде x = yg, y H2, g H. Изоморфизм H1 H2 ставит в соответствие элементу x H1 именно этот элемент y H2. Заметим, что любой элемент h H коммутирует с любым элементом из H1 H2. Поэтому

hx = h(yg) = yhg = xh = ygh,

т. е. элемент g коммутирует с любым элементом из H. Поэтому g H коммутирует с любым элементом из H1H = H2H = G, т. е. g лежит в центре группы G. Таким образом, прямо подобные нормальные подгруппы H1 и H2 центрально изоморфны, т. е. существует такой изоморфизм τ : H1 → H2, что x−1τ(x) лежит в центре группы G для любого x H1. Это условие, конечно же, не является достаточным условием прямого подобия подгрупп.

В решетке Ideal R всех идеалов некоторого кольца R два прямо подобных элемента I1 и I2 являются изоморфными кольцами: из

R = I1 J = I2 J

следует, что

I1 R/J I2.

Обозначим этот изоморфизм через τ и заметим, что для лю-

бого x I1

τ(x) − x J.

Поскольку по определению идеала IkJ, JIk Ik ∩ J = 0 для k = 1, 2, для всех элементов b J выполняется равенство

bx = xb = τ(x)b = bτ(x) = 0, x I1.

Отсюда следует, что b(τ(x)−x) = (τ(x)−x)b = 0, т. е. (τ(x)− x)R = R(τ(x) − x) = 0 для любого x I1. Такой изоморфизм называется аннуляторным. Таким образом, прямо подобные

59

элементы решетки идеалов кольца аннуляторно изоморфны. Обратное, очевидно, неверно.

Теорема 2.29 (Шмидта — Оре). Пусть A — модулярная решетка с композиционными рядами. Тогда любые два прямых -разложения единицы на неразложимые элементы из A прямо подобны.

Доказательство. Достаточно показать, что для любых двух прямых -разложений

где ai, bj неразложимы, существует такое j {1, . . . , m}, что

1 = bj × a2 × · · · × an.

Действительно, заменяя последовательно элементы a1, a2, . . . , an на подходящие bj1 , . . . , bjn , получаем прямое подобие разло-

жений (2.3).

Возможность искомой замены докажем индукцией по длине l(A) = d(1) композиционного ряда в решетке A. Если d(1) = 1, то решетка A состоит из двух элементов 0 и 1, поэтому утверждение очевидно. Допустим, возможность замены доказана для прямых -разложений наибольшего элемента в любой решетке с длиной композиционного ряда, меньшей чем d(1).

Зафиксируем два разложения (2.3). Для любых i = 1, . . . , n, j = 1, . . . , m обозначим

a¯i = a1 × · · · × ai−1 × ai+1 × · · · × an, bij = ai (bj a¯i),

Мы рассмотрим три случая: (1) существует j {1, . . . , m}

такое, что aj1 < bj; (2) b1i < a1 для любого i = 1, . . . , n; (3) aj1 = bj для любого j = 1, . . . , m, но существует i {1, . . . , n}

такое, что b1i = a1.

Случай 1. Пусть aj1 < bj для некоторого j {1, . . . , m}.

Рассмотрим

w = a11 · · · am1 .

60