Algebra3

Оглавление

3.3.Фильтры и ультрафильтры булевых алгебр ... 78

1

5.5.Вполне частично упорядоченные множества. Лемма Хигмана 1

6.1.Неприводимые представления и теорема Машке 129

7.3.Нильпотентность радикала артинова кольца . 147

2

§1. Алгебраические системы

1.1.Подалгебры и гомоморфизмы. Напомним из-

вестные понятия, встречавшиеся в курсе математической логики (основы теории моделей).

Сигнатурой называется пара F = (F, ν), где F — неко-

торое множество (функциональных символов),

ν: F → Z+ = {n Z | n ≥ 0}

—функция арности.

Алгебраической системой (или алгеброй) сигнатуры F

называется пара

A = (A, FA),

где A — некоторое непустое множество (носитель), а FA —

множество операций (интерпретация сигнатуры F в A):

оно состоит из отображений

fA : Aν(f) → A, f F.

Пусть A = (A, FA), B = (B, FA) — две алгебры сигнатуры F.

• Гомоморфизмом из A в B называется такое отображение ϕ : A → B, что

ϕ(fA(a1, . . . , aν(f))) = fB(ϕ(a1), . . . , ϕ(aν(f)))

для любых f F , ai A. В дальнейшем использование символов алгебраических систем A и B вместо символов множеств A и B будет означать, то отображение ϕ : A → B является гомоморфизмом A в B.

•Мономорфизмом называют инъективный гомоморфизм,

аэпиморфизмом — сюръективный, изоморфизмом — биек-

тивный. Отношение изоморфизма на алгебрах обозначается символом . Очевидно, если ϕ : →B, ψ : B → A — два

гомоморфизма и ϕ ◦ ψ = idA, ψ ◦ ϕ = idB — тождественные отображения, то ϕ и ψ — изоморфизмы и A B.

•Ядром гомоморфизма ϕ : A → B называется множество

Ker ϕ = {(a1, a2) A × A | ϕ(a1) = ϕ(a2)} A × A.

3

•Алгебра A называется подалгеброй алгебры B, если A B и отображение вложения является гомоморфизмом алгебры A в B (т. е. A B).

Легко видеть, что A B в том и только в том случае, когда A B — подмножество, замкнутое относительно всех операций fB, f F , причем fA = fB|A — индуцированные операции.

Поэтому, например, пересечение любого семейства подалгебр в данной алгебре снова является подалгеброй в данной алгебре

•Образ любого гомоморфизма ϕ : A → B является подалгеброй в B, обозначаемой через Im ϕ.

•Подалгебра, порожденная в алгебре A множеством

X — это наименьшая подалгебра в A, содержащая X (т.е. носитель которой содержит X как подмножество). Такую

подалгебру мы будем обозначать SgA(X). Она всегда существует, поскольку может быть построена как пересечение

всех подалгебр, содержащих X:

\

SgA(X) = B

B A

X B

Приведем «конструктивное» определение подалгебры, порожденной множеством.

Предложение 1.1. Пусть A = (A, FA) — алгебра, X A. Для любого подмножества Y A обозначим через EA(Y ) следующее множество:

n≥1

Доказательство. Докажем равенство (1.1).

Достаточно показать, что множество

[

C(X) = EAn(X)

n≥1

4

замкнуто относительно всех операций fA, f F : тогда это множество относительно индуцированных операций является подалгеброй в A, содержащей X EA(X), и SgA(X) содержится в C(X).

Любое конечное множество элементов из C(X) содержится в EAn(X) для некоторого достаточно большого n ≥ 1. Значение операции на этих элементах лежит в EAn+1(X) C(X), что и требовалось.

Очевидно, что если Y B для некоторой подалгебры

Определение 1.2. Пусть A — множество, P(A) — множество всех его подмножеств. Отображение C : P(A) → P(A) называется оператором замыкания, если для любых X, Y A

(1)X C(X);

(2)C2(X) = C(X);

(3)X Y C(X) C(Y ).

Подмножество X A называется замкнутым относительно оператора замыкания C, если X = C(X).

Оператор замыкания C называется алгебраическим, если замыкание любого множества совпадает с объединением за-

мыканий его конечных подмножеств:

[

Y X

|Y | < ω

Теорема 1.3. Пусть A — алгебра сигнатуры F. Тогда

C= SgA : P(A) → P(A)

—алгебраический оператор замыкания.

Доказательство. Проверим свойства (1)–(3) определения 1.2 для C = SgA: X C(X) и C2(X) = C(X) по определению подалгебры, порожденной множеством. Если X Y ,

то C(Y ) Y X, и поэтому C(Y ) C(X). Следовательно,

5

C — оператор замыкания. Подмножества, замкнутые относительно этого оператора, соответствуют подалгебрам в A.

Следует из свойства (3) любого оператора замыкания.

Индукцией по n покажем, что любой элемент a EAn(X),

n ≥ 1, содержится в правой части ( ). Если n = 1, то либо a X, либо a = fA(a1, . . . , aν(f)) для некоторых f F ,

Следующее утверждение является в некотором смысле обратным теореме 1.3: мы покажем, что условие (1.2) в точности характеризует операторы замыкания, которые задаются алгебраической структурой на множестве.

Теорема 1.4. Пусть A — непустое множество, C : P(A) → P(A) — алгебраический оператор замыкания. Тогда най- дется алгебра A с носителем A такая, что SgA = C.

6

Доказательство. Выберем сигнатуру следующим образом:

F= {fB,b | B A, |B| < ω, b C(B)},

ν(fB,b) = |B|.

Пусть |B| = n ≥ 1, b C(B), a1, . . . , an A. Положим

Если B = , то fA,b = b, b C( ) A, — константы (0-арные операции).

Легко видеть, что по построению алгебры A = (A, FA)

EA(X) = C(X), X A.

Если a EA(X), то a X или a = fB,bA (x1, . . . , xn), n =

|B|, xi X, b C(B). Если a X, то a C(X) по свойству

(1) определения 1.2. Если a EA(X) \ X, то a = b C(X) по построению.

Если b C(X), то ввиду алгебраичности оператора C найдется конечное подмножество Y X такое, что b

C(Y ). Если Y = {a1, . . . , am}, ai X, то b = fY,bA (a1, . . . , am)

EA(X).

Далее, по индукции получаем

EAn(X) = EA(C(X)) = C(C(X)) = C(X), n ≥ 1.

Определение 1.5. Пусть A — алгебра сигнатуры F. Конгруэнцией на A называется бинарное отношение эквивалентности θ A × A такое, что для любого f F , n = ν(f), и

для любых ai, bi A, i = 1, . . . , n,

(ai, bi) θ, i = 1, . . . , n (fA(a1, . . . , an), fA(b1, . . . , bn)) θ.

(1.3)

7

Например, конгруэнциями всегда являются отношения

Обозначим через Cong A множество всех конгруэнций алгебры A. Очевидно, Cong A замкнуто относительно пересе-

гда

(1)Ядро любого гомоморфизма ϕ : A → B является конгруэнцией на A.

(2)Для любой конгруэнции θ на A найдутся алгебра B

иэпиморфизм ϕ : A → B такие, что Ker ϕ = θ.

Доказательство. (1) Пусть ϕ : A → B, θ = Ker ϕ. По определению ядра (a, b) θ ϕ(a) = ϕ(b). Рефлексивность, симметричность и транзитивность этого отношения очевидны.

Если f F , ai, bi A, (ai, bi) θ, i = 1, . . . , n = ν(f), то ϕ(fA(a1, . . . , an)) = fB(ϕ(a1), . . . , ϕ(an)) = ϕ(fA(b1, . . . , bn)).

(2) Построим подходящую алгебру B на носителе

A/θ = a/θ = {x A | (a, x) θ} | a A

— множестве классов эквивалентности в A относительно θ. Интерпретацию сигнатуры осуществим следующим образом: для f F , ν(f) = n, положим

fB(a1/θ, . . . , an/θ) = fB(a1, . . . , an)/θ, ai A.

Это определение корректно — оно не зависит от выбора представителей ai классов эквивалентности ai/θ, поскольку

ai/θ = bi/θ (ai, bi) θ,

а θ удовлетворяет (1.3).

Построенная алгебраическая система называется факторалгеброй алгебры A по конгруэнции θ и обозначается A/θ. Отображение ϕ : A → A/θ, действующее по правилу ϕ(a) =

8

a/θ, a A, является эпиморфизмом A в A/θ. Это отображе-

ние называется естественным гомоморфизмом и обознача-

ется через τθ. По определению очевидно, что Ker τθ = θ.

Рассмотрим один частный класс алгебраических систем. Пусть G — группа, т. е. алгебра сигнатуры F = {·, e, −1}, ν(·) = 2, ν(e) = 0, ν(−1) = 1, в которой для любых элементов

a, b, c G выполняются хорошо известные равенства

a · (b · c) = (a · b) · c, a · e = e · a = a, a · a−1 = a−1 · a = e.

Для некоторой конгруэнции θ на G рассмотрим множество

Nθ = {a · b−1 | (a, b) θ} G.

Покажем, что Nθ соответствует подгруппе в G. Отныне мы

т. е. (ab−1)(cd−1) Nθ. Далее,

ab−1 Nθ (a, b) θ (b, a) θ ba−1 = (ab−1)−1 Nθ.

Наконец, e Nθ в силу рефлексивности θ. Таким образом, Nθ замкнуто относительно операций G.

Более того, если h = ab−1 Nθ, x G, то xhx−1 = xab−1x−1 = (xa)(xb)−1 Nθ,

т. е. Nθ соответствует нормальной подгруппе в G.

Упражнение. Покажите обратное: любая нормальная подгруппа N E G определяет конгруэнцию

θN = {(hx, x) | x G, h N}

на G.

Упражнение. Покажите, что конгруэнции ассоциативного кольца (как алгебры с функциональными символами F = {+, ·, 0, −},

9

удовлетворяющей известным аксиомам) находятся во взаимнооднозначном соответствии с идеалами этого кольца.

Упражнение. Убедитесь, что известные конструкции факторгруппы и фактор-кольца являются частными случаями факторалгебр по конгруэнции.

К сожалению, далеко не всегда конгруэнции алгебраической системы можно хорошо описать некоторым подмножеством в этой системе. Это можно сделать, например, в случае групп, колец, векторных пространств и алгебр над полем, модулей над кольцом. Для полугрупп, булевых алгебр и решеток такого описания не существует.

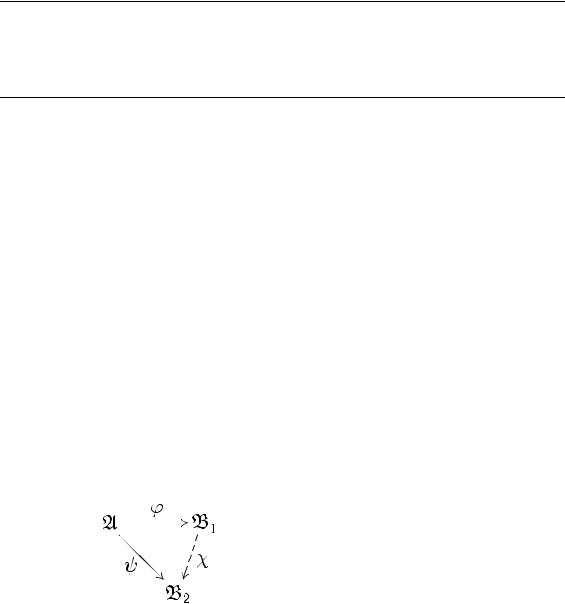
Теорема 1.7 (о гомоморфизмах). Пусть A, B1, B2 — ал-

гебры сигнатуры F, ϕ : A → B1 — эпиморфизм, ψ : A → B2 — гомоморфизм. Тогда Ker ϕ Ker ψ в том и только в том случае, когда существует гомоморфизм χ : B1 → B2 такой, что ϕ ◦ χ = ψ.

Более наглядно смысл этой теоремы можно продемонстрировать при помощи диаграммы.

χ Ker ϕ Ker ψ

Доказательство. Пусть Ker ϕ Ker ψ. Определим χ :

B1 → B2 следующим образом: для данного b B1 выберем любой элемент a из непустого множества {x A | ϕ(x) = b} A и положим χ(b) = ψ(a) B2. Результат не зависит от выбора элемента a: если ϕ(a) = b = ϕ(a′), то (a, a′) Ker ϕ Ker ψ, т. е. ψ(a) = ψ(a′). Соотношение ϕ ◦ χ = ψ выполнено по построению. Способ построения гомоморфизма χ показан на диаграмме.

10