Algebra3

Очевидно, что полученное в результате любого из этих действий множество определяющих соотношений порождает ту же конгруэнцию, что и исходное.

Пример 4.23. Пусть X = {x, y, e} и

S = {hx4, ei, hy2, x2i, hx3y, yxi, hez, zi, hze, zi | z X}.

Построим конфлюэнтную переписывающую систему, порождающую ту же конгруэнцию, что и S. Зафиксируем порядок ≤deg-lex на X , полагая e < x < y.

1. Композиция пересечения hx4, ei и hx3y, yxi по подслову x3 равна hxyx, eyi. Слово xyx терминальное в G = G(X, S),

TG (ey) y.

Заметим, что остальные композиции пересечения этих пар (по подсловам x2, x) тривиальны в G(X, S).

Композиция пересечения hx3y, yxi с hy2, x2i по подслову y равна hx5, yxyi. Слово yxy терминальное в G = G(X, S), а

TG (x5) x. Строим S1 = S {hyxy, xi, hxyx, yi}.

2. Композиция пересечения hx3y, yxi с hxyx, yi по подслову xy равна hyx2, x2yi: оба слова терминальные в графе

G(X, S1). Строим S2 = S1 {hyx2, x2yi}.

Непосредственной проверкой всех композиций можно убедиться, что все композиции всех пар из S2 тривиальны в G3 = G(X, S2). Следовательно, S2 — конфлюэнтная переписывающая система, и элементы полугруппы A = SmghX | Si находятся во взаимно-однозначном соответствии с терминальными вершинами графа G3. Слова, соответствующие этим вершинам, легко перечислить: это все слова, не содержащие подслов, встречающихся среди левых частей пар из S2, т. е., в данном случае, не содержащие подслов вида

ee, ex, xe, ey, ye, x4, y2, yx2, xyx, yxy, x3y.

Легко заметить, что таких слов конечное число:

e, x, y, x2, xy, yx, x3, x2y.

Таким образом, A — полугруппа из 8 элементов.

101

Порядок ≤ на множестве слов X играет вспомогательную роль: он необходим для того, чтобы обеспечить сохранение переписывающего свойства системы определяющих соотношений при добавлении новых пар. В следующем примере мы покажем, что выбор наиболее удобного порядка существенно упрощает вычисления.

Пример 4.24. Пусть X = {a, b, e},

S = {han, ei, hb2, ei, habab, ei, hez, zi, hze, zi | z X}, n ≥ 2.

Зафиксируем башенный порядок на множестве X , пола-

гая X1 = {e, a}, X2 = {b}. Множество X1 = {a, e} упорядочим по правилу deg-lex, полагая e < a.

1. Рассмотрим композицию пересечения han, ei с habab, ei

по подслову a: она равна hebab, an−1i. Выберем bab TG(X,S)(ebab) и положим S1 = S hbab, an−1i.

2. Заметим, что композиция включения hbab, an−1i в habab, ei тривиальна. Поэтому пару habab, ei можно исключить из S1. Полученная система определяющих соотношений S1′ =

S\ {habab, ei} эквивалентна исходной.

3.Композиция пересечения hbab, an−1i с hb2, ei по под-

слову b равна hbae, an−1bi. Следовательно, строим S2 = S1 {hba, an−1bi}. Композиция включения добавленной пары с hbab, an−i тривиальна, поэтому положим S2′ = S2\{hbab, an−1i}. Построенная система

S2′ = {han, ei, hb2, ei, hba, an−1bi, hez, zi, hze, zi | z X}

является конфлюэнтной.

Слова, редуцированные относительно S2′ (терминальные вершины орграфа G(X, S2′ )), легко перечислить:

e, a, a2, . . . , an−1, b, ab, a2b, . . . , an−1b.

Таким образом, SmghX | Si — полугруппа из 2n элементов.

Заметим, что полугруппы из примеров 4.20, 4.23, 4.24 являются группами.

102

4.6. Конгруэнции групп. Пусть Gr — многообразие групп, т. е. алгебраических систем, сигнатура которых содержит бинарную операцию ·, унарную операцию −1 и константу e, удовлетворяющих хорошо известным аксиомам.

Любую группу G можно рассматривать как полугруппу относительно одной лишь бинарной операции. Обозначим такую полугруппу Gsmg.

Лемма 4.25. 1. Пусть ϕ: G1 → G2 — гомоморфизм групп.

Тогда то же самое отображение ϕ является гомоморфизмом полугрупп Gsmg1 → Gsmg2 .

2. Пусть G — группа, A — полугруппа, ϕ: Gsmg → A — сюръективный гомоморфизм полугрупп. Тогда на множе- стве A можно определить структуру группы A′, причем A′smg = A, а ϕ — гомоморфизм групп G → A′.

Доказательство этого утверждения является легким упражнением.

Пусть X — некоторое (возможно пустое) множество, A = SmghY | S0(X)i — полугруппа из примера 4.20.

По теореме 4.14 множество A можно отождествить с множеством слов из Y , редуцированных относительно S0(X). Определим операцию

˜: Y → Y , u = y1 . . . yn 7→u˜ = y˜n . . . y˜1,

u A. Тогда F(X) = (A, ·, −1, e), очевидно, является группой

(причем F(X)smg = A).

Теорема 4.26. Группа F(X) изоморфна свободной группе GrhXi, порожденной множеством X.

Доказательство. Для любого множества X имеют место вложения X Y , X GrhXi (многообразие групп не

103

тривиально). Введем отображение α : Y → GrhXi такое, что

α(e) = e, α(x) = x, α(˜x) = x−1, x X.

Лемма 4.27. Полугруппа GrhXismg порождена множеством

α(Y ) = {α(y) | y Y }.

Доказательство. Рассмотрим последовательность множеств En(X) GrhXi, n ≥ 0, определенную правилом

E0(X) = X {e}, En+1(X) = En(X) {fg, f−1 | f, g En(X)}.

Это возрастающая последовательность множеств, использовавшаяся для построения оператора замыкания. Поскольку

группа GrhXi порождена множеством X, имеем

[

En(X) = GrhXi.

n≥0

С другой стороны, объединение последовательности множеств En′ (Y ) GrhXi, n ≥ 0, такой, что

E0′ (Y ) = α(Y ), En′ +1(Y ) = En′ (Y ) {fg | f, g En′ (Y )},

совпадает с полугруппой, порожденной множеством α(Y ) в GrhXismg.

Индукцией по n покажем, что En(X) En′ (Y ). Дей-

ствительно, X = E0(X) E0′ (Y ) = α(Y ). Предположим, h En(X) \ En−1(X), n > 0. Тогда либо h = fg, либо h = f−1, f, g En−1(X). В первом случае h En′ (Y ), по-

скольку En−1(X) En′ −1(Y ) по предположению индукции. Во втором случае имеем три варианта: либо f = x (n = 1),

либо f = g1g2, либо f = g−1, g1, g2 En−2(X) E′ − (Y ).

1 n 2

В первом варианте h = x−1 α(Y ) = E0′ (Y ), во втором —

h = g−1g−1, g−1 E′ − (Y ) по предположению индукции. По-

2 1 i n 1

следний вариант невозможен, поскольку тогда h = f−1 = g1 En−2(X) En−1(X), что противоречит выбору h.

Обозначим через τ : SmghY i → SmghY | S0(X)i = F(X)smg естественный гомоморфизм полугрупп с ядром θS0(X). Согласно определению групповой структуры на F(X) τ(x)−1 = τ(˜x), x X, τ(e) = e — единица этой группы.

По универсальному свойству SmghY i существует гомоморфизм полугрупп ϕ: SmghY i → GrhXismg такой, что ϕ(y) =

104

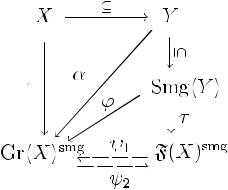
α(y) для y Y . Легко проверить, что ϕ(u) = ϕ(v) для любой пары hu, vi S0(X). Поэтому Ker ϕ Ker τ и по теореме о гомоморфизмах существует гомоморфизм полугрупп ψ1 : F(X)smg → GrhXismg такой, что ϕ = ψ1τ (см. диаграмму).

С другой стороны, F(X) является группой, поэтому по универсальному свойству свободной группы отображение X

τ

Y SmghY i → F (X) продолжается до гомоморфизма групп

ψ2 : GrhXi → F(X).

Рассмотрим суперпозицию отображений ι = ψ2ψ1 : F(X)smg → F(X)smg. Для любого y Y имеем

Следовательно, ι = id и, в частности, гомоморфизм ψ1 инъективен.

По лемме 4.27 гомоморфизм ϕ и, следовательно, ψ1 сюръективны. Искомый изоморфизм найден.

Таким образом, существует взаимно-однозначное соответствие между элементами свободной группы F = GrhXi, порожденной множеством X, и словами в алфавите Y =

105

Упражнение. Покажите, что если X1, X2 — конечные множества и GrhX1i GrhX2i, то |X1| = |X2|.

Теорема 4.28. Для любого множества определяющих со- отношений S

GrhX | Sismg SmghY | S S0(X)i.

Доказательство. Обозначим через τ1 : SmghY i → SmghY |

S S0(X)i и τ2 : GrhXi → GrhX | Si естественные гомоморфизмы полугрупп и групп соответственно. Поскольку τ2 сюръективно, полугруппа GrhX | Sismg порождена множеством τ2(α(Y )). Заметим также, что полугруппа SmghY | S S0(X)i есть гомоморфный образ GrhXismg и, следовательно, является группой.

По универсальному свойству полугруппы SmghY i и группы GrhXi существуют гомоморфизмы ϕ1 : SmghY i → GrhX |

Sismg, ϕ2 : GrhXismg → SmghY | S S0(X)i такие, что ϕ1(y) = τ2(α(y)), ϕ2(x) = τ1(x), x X, y Y .

Легко установить, что Ker τ1 Ker ϕ1, следовательно, по теореме о гомоморфизмах существует ψ1 : SmghY | S S0(X)i → GrhX | Sismg — такой гомоморфизм полугрупп,

что ψ1τ1 = ϕ1.

По лемме 4.27 GrhXismg порождена (как полугруппа) элементами множества α(Y ). Следовательно, GrhX | Sismg порождена множеством τ2(α(Y )) = ϕ1(Y ) = ψ1(τ1(Y )). Следовательно, ψ1 сюръективен.

С другой стороны, ϕ2 сюръективен и, следовательно, является гомоморфизмом групп. Существует гомоморфизм (полу)групп ψ2 : GrhX | Sismg → SmghY | S S0(X)i такой, что ψ2τ2 = ϕ2.

106

Следовательно и гомоморфизм инъективен

Пример 4.29. Рассмотрим H = GrhX | Si, где X = {x, y},

S = {hx4, ei, hy2, x2i, hx3y, yxi}.

По теореме 4.28

Hsmg SmghY | S S0(X)i, Y = {x, y, x,˜ y,˜ e}.

Введем башенный порядок на Y , разбивая алфавит на две части Y1 = {x, y, e}, Y2 = {x,˜ y˜} и полагая e < x < y, x˜ < y˜.

Вычисляя те же композиции, что в примере 4.23, получаем, что система определяющих соотношений S1 = S S0(X) порождает ту же конгруэнцию, что S1′ S0(X), где

S1′ = {hx4, ei, hy2, x2i, hx3y, yxi, hyxy, xi, hxyx, yi, hyx2, x2yi}.

1. Вычислим композицию пересечения hxx,˜ ei с hx4, ei: она равна hex3, xe˜ i, что приводится к hx,˜ x3i.

Рассмотрим композицию пересечения hy2, x2i с hyy,˜ ei, приводящую к hx2y,˜ yi. Пересечение hx4, ei с hx2y,˜ yi дает пару hy,˜ x2yi.

Строим

S2 = S1′ {hx,˜ x3i, hx2y,˜ yi, hy,˜ x2yi} S0(X).

107

Эта система определяющих соотношений полугруппы Hsmg, из которой при помощи (тривиальных) композиций включения можно исключить все пары, содержащие x˜ и y˜, кроме hx,˜ x3i, hy,˜ x2yi.

3. Таким образом, Hsmg SmghY | S3i, где

S3 = {hx4, ei, hy2, x2i, hx3y, yxi, hyxy, xi, hxyx, yi, hyx2, x2yi, hx,˜ x3i, hy,˜ x2yi, hex, xi, hxe, xi, hey, yi, hye, yi, hee, ei}

— базис Гр¨ебнера — Ширшова соответствующей полугруппы. Все слова, редуцированные относительно S3, указаны в примере 4.23. Построенная группа H изоморфна подгруппе

мультипликативной группы тела кватернионов

H = R + Ri + Rj + Rk,

i2 = j2 = k2 = ijk = −1,

состоящей из элементов {1, −1, i, −i, j, −j, k, −k}.

Пример 4.30. Рассмотрим следующую задачу: найти систему порождающих элементов и определяющих соотношений для группы Dn преобразований симметрии правильного n-угольника (группы диэдра).

По определению элементами этой группы являются всевозможные движения плоскости (т. е. преобразования, сохраняющие длины и углы), которые действуют как перестановки на множестве вершин правильного n-угольника. Занумеруем вершины последовательно по часовой стрелке числами 1, . . . , n.

Очевидно, что центр (пересечение срединных перпендикуляров к сторонам) n-угольника неподвижен при любом преобразовании симметрии. Хорошо известно, что любое движение с одной неподвижной точкой является линейным и, следовательно, ортогональным преобразованием. Любое линейное преобразование плоскости однозначно определяется образами двух неколлинеарных векторов.

Рассмотрим векторы a1, a2, соответствующие вершинам 1 и 2 (начинающиеся в центре симметрии). Образы этих векторов соответствуют соседним вершинам k, k+1. Возможны два случая:

108

1)a1 7→ak, a2 7→ak+1 — в этом случае преобразование симметрии есть поворот на угол 2π(k − 1)/n по часовой стрелке;

2)a1 7→ak+1, a2 7→ak — в этом случае преобразование симметрии есть суперпозиция зеркального отражения относительно срединного перпендикуляра к стороне, соединяющей вершины 1 и 2, и поворота на угол 2π(k−1)/n по часовой стрелке.

Таким образом, любое преобразование симметрии правильного n-угольника может быть получено из преобразования R поворота на угол 2π/n по часовой стрелке и преобра-

зования S зеркального отражения. Именно, любое преобразование имеет вид Rk−1 или Rk−1S, k = 1, . . . , n, поэтому

|Dn| = 2n.

Легко заметить, что преобразования R и S удовлетворяют соотношениям

Таким образом, группа Dn обязана быть гомоморфным образом группы

G = Grha, b | han, ei, hb2, ei, habab, eii.

Действительно, рассмотрим отображение α : {a, b} → Dn, a 7→R, b 7→S. По универсальному свойству свободной группы существует сюръективный гомоморфизм ϕ: Grha, bi → Dn такой, что ϕ(a) = R, ϕ(b) = S. В силу (4.5) ядро гомоморфизма ϕ содержит все определяющие соотношения группы G. По теореме о гомоморфизмах существует сюръекция ψ : G → Dn такая, что ψτ = ϕ.

Построение базиса Гр¨ебнера — Ширшова для группы G фактически проведено в примере 4.24. Поэтому группа G состоит из 2n элементов, |G| = |Dn| и, следовательно, G Dn.

109

§5. Кольца и модули

5.1.Свободные кольца. Обозначим через Rng многообразие (ассоциативных) колец, т. е. алгебр сигнатуры

+, −, 0, ·, удовлетворяющих хорошо известным тождествам. В частности, если R = (R, +, −, 0, ·) Rng, то Rsmg := (R, ·) — полугруппа. Если R1, R2 Rng, ϕ : R1 → R2 — гомоморфизм колец, то это же отображение ϕ является гомоморфизмом полугрупп Rsmg1 → Rsmg2 , который мы обозначим

через ϕsmg.

Обратно, любая полугруппа может быть вложена в кольцо: если A Smg, то полугрупповое кольцо ZA из п. 4.2 содержит полугруппу A. Следующая лемма показывает, что эта конструкция в определенном смысле универсальна.

Лемма 5.1. Пусть A Smg, R Rng, ϕ : A → Rsmg —

гомоморфизм полугрупп. Тогда существует гомоморфизм колец ψ : ZA → R такой, что ψ(u) = ϕ(u) для u A.

Среди колец часто выделяют класс таких, в которых есть нейтральный по умножению элемент (единица). Эти кольца образуют многообразие алгебр сигнатуры +, −, 0, ·, 1 (с добавленной константой 1), удовлетворяющих хорошо известным аксиомам. Обозначим это многообразие через Rng#. Если в кольце с единицей R Rng# «забыть» о существовании единицы, то получится кольцо из многообразия Rng, которое мы будем обозначать через R . Очевидно, что если ϕ : R1 → R2 — гомоморфизм колец с единицей, то это же отображение является гомоморфизмом колец R1 → R2 многообразия Rng.

Обратно, любое R Rng может быть вложено в кольцо с единицей. Достаточно рассмотреть множество R# = R × Z и определить на нем операции по правилам

(a, n) + (b, m) = (a + b, n + m), −(a, n) = (−a, −n),

(a, n)(b, m) = (ab + nb + ma, nm)

110