Algebra3

Убедимся, что a b = sup{a, b}. Действительно, a b — верхняя грань множества {a, b}, поскольку

a (a b) = a, b (a b) = b (b a) = b

по (Р2) и (Р4). Если c — какая-то верхняя грань множества

{a, b}, то

a c = c, b c = c,

поэтому

(a b) c = a (b c) = a c = c,

что означает a b ≤ c.

Равенство a b = inf{a, b} проверяется аналогично.

Таким образом, мы можем рассматривать решетки как алгебры класса L, на которых отношение ≤ определено по правилу

a ≤ b a b = a a b = b.

Понятия подрешетки и гомоморфизма решеток имеют обычный алгебраический смысл. Поскольку класс L определяется семейством тождеств (Р1)–(Р4), он является многообразием.

Пример 2.4. Множество P(M) всех подмножеств данного множества M относительно частичного порядка является решеткой. При этом A B = A ∩ B, A B = A B.

Пример 2.5. Множество N натуральных чисел с отношением делимости

n | m q N : m = nq

является решеткой. При этом n m = н.о.к.(n, m), n m =

н.о.д.(n, m).

Пример 2.6. Пусть B — алгебра некоторой сигнатуры F,

где S — оператор из раздела 1.5. Множество Sub B состоит из множеств-носителей подалгебр алгебры B, к которым добавляется пустое множество в том случае, когда сигнатура

41

Например, решетки (P(M), ) и (N, |) дистрибутивны. Действительно, равенство

X ∩ (Y Z) = (X ∩ Y ) (X ∩ Z)

для множеств хорошо известно. Для натуральных чисел x, y, z искомое равенство

н.о.д.(x, н.о.к.(y, z)) = н.о.к.(н.о.д.(x, y), н.о.д.(x, z))

легко проверить, пользуясь каноническим разложением натуральных чисел на простые множители.

Дистрибутивные решетки образуют многообразие, содержащееся в многообразии L всех решеток. В частности поэтому если некоторая решетка A содержит не дистрибутивную подрешетку, то A не является дистрибутивной.

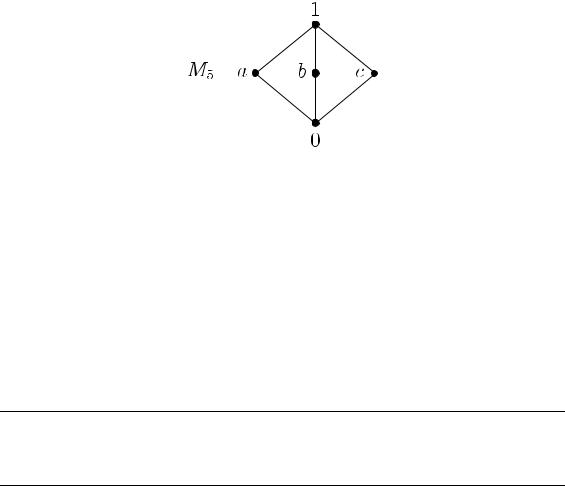
Примером не дистрибутивной решетки является множество M5 = {0, 1, a, b, c}, где 0 — наименьший элемент, 1 — наибольший элемент, a, b, c не сравнимы между собой. Эту решетку можно изобразить в виде следующей диаграммы.

Пример 2.9. Для симметрической группы S3 решетка Sub S3 не дистрибутивна.

Действительно, отображение ϕ : M5 → Sub S3, при кото-

ром

ϕ(0) = {e}, ϕ(1) = S3, ϕ(a) = h(12)i, ϕ(b) = h(13)i, ϕ(a) = h(23)i,

является инъективным гомоморфизмом решеток. Следовательно, Sub S3 содержит подрешетку, изоморфную M5 и не является дистрибутивной.

Упражнение. Пусть G — группа, R — кольцо. Покажите, что решетки (Norm G, ) и (Ideal R, ), вообще говоря, не являются дистрибутивными.

43

Дистрибутивность является весьма сильным условием на решетку. Мы знаем, что решетка (P(M), ) дистрибутивна, и, следовательно, таковы же все ее подрешетки. Следующая теорема устанавливает, что (с точностью до изоморфизма) других дистрибутивных решеток нет.

Теорема 2.10. Пусть A — дистрибутивная решетка. То- гда найдется множество M и подрешетка B P(M) такие, что A B.

Доказательство. Без ограничения общности можно полагать, что решетка A содержит наименьший элемент 0 A. В самом деле, если в A нет наименьшего элемента, рассмотрим A# = A {0}, 0 / A, и доопределим

x 0 = x, x 0 = 0, x A#.

Легко проверить, что получается дистрибутивная решетка A#, в которой A является подрешеткой. Доказав теорему для A#, мы докажем ее и для исходной A.

Поэтому с самого начала предположим, что A обладает наименьшим элементом 0 A. Прежде чем приступить к построению множества M и вложения A в P(M), сделаем ряд предварительных замечаний.

Идеалом решетки A называется такое множество I A, что

a, b I a b I, a I x A a x I.

Второе из этих условий эквивалентно следующему:

a I x A (x ≤ a x I).

Например, для любого u A множество u↓ = {x A | x ≤ u}

является идеалом в A, содержащим u. Действительно, если a, b u↓, то

(a b) u = a (b u) = a u = u,

т. е. a b u↓. Если a u↓ и x ≤ a, то x ≤ u, т. е. x u↓. Если решетка A дистрибутивна, I1, I2 — идеалы в A, то

I = I1 I2 = {a b | a I1, b I2}

44

тоже является идеалом в A. Действительно, если a1 b1, a2 b2 I, то

(a1 b1) (a2 b2) = (a1 a2) (b1 b2) I1 I2 = I,

и для любого x A

(a1 b1) x = (a1 x) (b1 x) I1 I2 = I.

также является идеалом в A. Действительно, если a, b I, то a, b Ik для достаточно большого k ≥ 1, поэтому a b Ik, a x Ik для любого x A.

Продолжим доказательство теоремы. Если |A| = 1, то утверждение очевидно. В противном случае рассмотрим

M = {(a, b) A × A | a 6≤b} 6= .

Для каждой пары (a, b) M рассмотрим множество Ma,b, состоящее из всех таких идеалов I в решетке A, что b I, a / I. Это множество непусто (b↓ Ma,b) и удовлетворяет условию леммы Цорна (принципа максимума): если I1 I2 . . . — цепь идеалов, Ik Ma,b, то объединение этой цепи тоже является идеалом, содержащим b и не содержащим a. Следовательно, существует максимальный идеал Ia,b Ma,b. Этот идеал обладает следующими свойствами:

b Ia,b, a / Ia,b, Ia,b I a I

для любого идеала I в A.

Зафиксируем для каждой пары (a, b) M такой идеал Ia,b и определим отображение

ϕ : A → P(M)

по правилу

ϕ(x) = {(a, b) M | x / Ia,b}.

45

Остается показать, что ϕ — инъективный гомоморфизм решеток.

Покажем инъективность. Пусть x, y A, x 6= y, т. е. x 6≤y или y 6≤x. Допустим, x 6≤y. Тогда (x, y) M, x / Ix,y и y Ix,y в силу выбора идеала Ix,y, следовательно,

(x, y) ϕ(x), (x, y) / ϕ(y)

иϕ(x) 6= ϕ(y). Случай y 6≤x полностью аналогичен. Покажем сохранение операции , т. е.

соответственно означает (a, b) ϕ(x) или (a, b) ϕ(y). Обратно, если (a, b) ϕ(x) или (a, b) ϕ(y), то x / Ia,b

или y / Ia,b соответственно. Но x ≤ x y и y ≤ x y, поэтому если x y Ia,b, то x, y Ia,b. Следовательно, x y / Ia,b, что означает (a, b) ϕ(x y).

Покажем сохранение операции , т. е.

ϕ(x y) = ϕ(x) ∩ ϕ(y).

Вложение « » доказывается легко. Если (a, b) ϕ(x y), то

x y / Ia,b. Допустим, (a, b) / ϕ(x) ∩ ϕ(y). Тогда x Ia,b

или y Ia,b. Но x y ≤ x и x y ≤ y, поэтому x y Ia,b, — противоречие.

Поскольку x Ix, y Iy, то эти идеалы строго больше, чем Ia,b, следовательно, a Ix и a Iy (идеал Ia,b был выбран максимальным среди таких, что a / Ia,b). Таким образом,

46

где z1, z2 Ia,b, u1 ≤ x, u2 ≤ y. Тогда

a = a a = (z1 u1) (z2 u2)

= (z1 z2) (z1 u2) (u1 z2) (u1 u2) (2.1)

в силу дистрибутивности. Здесь

z1 z2 ≤ z1 Ia,b, z1 u2 ≤ z1 Ia,b, u1 z2 ≤ z2 Ia,b

и

(u1 u2) = (u1 x) (u2 y) = (u1 u2) (x y) ≤ x y Ia,b

Следовательно, правая часть (2.1) лежит в Ia,b, что противоречит a / Ia,b.

Упражнение. Докажите, что любая конечная дистрибутивная решетка вкладывается в решетку (N, |). Верно ли это для счетной дистрибутивной решетки?

2.3. Модулярные (дедекиндовы) решетки. Многие важные решетки, встречающиеся на практике, не являются дистрибутивными, но удовлетворяют более слабому свойству модулярности.

Определение 2.11. Решетка A называется модулярной, если

Замечание 2.12. В любой решетке выполняется импликация

a ≤ b a (b c) ≤ b (a c).

Действительно,

a ≤ b, a ≤ a c a ≤ b (a c), b c ≤ c ≤ a c,

b c ≤ b, b c ≤ a c b c ≤ b (a c),

и поэтому

a (b c) ≤ b (a c).

Из следующего утверждения вытекает, что класс модулярных решеток образует многообразие.

47

Предложение 2.13. Для решетки A следующие условия эквивалентны:

(1)A модулярная;

(2)A |= x1 ((x1 x2) x3) ≈ (x1 x2) (x1 x3);

(3)A |= x1 ((x1 x2) x3) ≈ (x1 x2) (x1 x3).

Доказательство. (1) (2) Так как a b ≤ a для любых a, b A, то из (2.2) следует, что

a ((a b) c) = (a b) (a c),

т. е. выполняется условие (2).

(2) (1) Пусть a, b, c A, a ≤ b. Тогда b a = a и

a (b c) = (b a) (b c) = b ((b a) c) = b (a c).

Эквивалентность (1) (3) доказывается аналогично.

Следствие 2.14. Подрешетка или гомоморфный образ мо- дулярной решетки является модулярной решеткой. Прямое произведение семейства модулярных решеток является мо- дулярной решеткой.

Следствие 2.15. Любая дистрибутивная решетка моду- лярна.

Доказательство. Условия (2) и (3) в предложении 2.13 следуют соответственно из тождеств дистрибутивности (Д2) и (Д1) п. 2.2. Например, условие (Д1) для решетки A влечет

Существуют модулярные, но не дистрибутивные решетки. Примером является решетка M5 из п. 2.2.

Пример 2.16. (1) Для линейного пространства V над некоторым полем решетка Sub V является модулярной.

(2)Для группы G решетка Norm G является модулярной.

(3)Для кольца R решетка Ideal R является модулярной.

48

Напомним, что в этих решетках операция — это обычное теоретико-множественное пересечение; операция в решетках Sub V и Ideal R — это сумма подпространств (идеалов), а в решетке Norm G — произведение нормальных подгрупп.

Проверим, например, условие модулярности для Ideal R.

Пусть a = I1, b = I2, c = I3, I1, I2, I3 E R, причем I1 I2.

Тогда

a (b c) = I1 + (I2 ∩ I3), b (a c) = I2 ∩ (I1 + I3).

В силу замечания 2.12 достаточно показать, что

I1 + (I2 ∩ I3) I2 ∩ (I1 + I3)

Пусть x I2 ∩ (I1 + I3), т. е. x = y + z I2, y I1 I2, z I3. Тогда z = x − y I2, что означает z I2 ∩ I3. Таким образом, x = y + z I1 + (I2 ∩ I3).

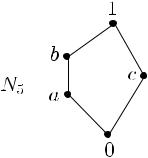
Пример 2.17. (1) Примером не модулярной решетки является решетка N5, схематическое изображение которой приведено на следующей диаграмме:

(2) Решетка Sub G всех подгрупп группы G, вообще говоря, не является модулярной.

Действительно, в решетке Sub S4 содержится подрешетка, изоморфная решетке N5. Проверим, что отображение N5 → Sub S4, заданное правилом

является инъективным гомоморфизмом решеток. Инъективность очевидна, нужно проверить сохранение операций и

49

. В проверке нуждается только равенство h(12)i h(234)i = S4. Это следует из того, что

(12)(234) = (13), (13)(234) = (14),

а транспозиции (12), (13), (14), как известно, порождают группу S4.

Пример 2.18. Решетки, рассмотренные в примере 2.16 изоморфны решеткам конгруэнций соответствующих алгебраических систем. Может возникнуть подозрение, что решетки конгруэнций алгебраических систем модулярны. Это, вообще говоря, неверно.

Рассмотрим алгебраическую систему X = ({1, 2, 3, 4}, fX), ν(f) = 1, где операция f задана следующим образом:

f(1) = 2, f(2) = 1, f(3) = 4, f(4) = 3.

Кроме = {(i, i) | i = 1, 2, 3, 4} и = {1, 2, 3, 4}2, следующие множества являются конгруэнциями алгебры X:

θ1 = {(1, 2), (2, 1)}, θ2 = θ1 {(3, 4), (4, 3)}, θ3 = {(2, 3), (3, 2), (1, 4), (4, 1)}

(напомним, что в данном случае конгруэнция — это такое отношение эквивалентности θ, что (i, j) θ (f(i), f(j))

θ).

Легко установить, что отображение N5 → Cong X, заданное правилом

0 7→ , 1 7→ ,

a 7→θ1, b 7→θ2, c 7→θ3,

является инъективным гомоморфизмом решеток, т. е. Cong X не модулярна.

Определение 2.19. Пусть A — решетка, a, b A, a ≤ b. Множество

[a, b] = {x A | a ≤ x ≤ b}

называется интервалом решетки A. Интервал [a, b] называется простым, если |[a, b]| = 2, т. е. он содержит только два элемента a и b, a < b.

50