3. Вычисление доверительных интервалов статистических параметров

Цель – научить студентов алгоритмам вычисления доверительных интервалов статистических параметров.

При статистической обработке данных вычисленные средняя арифметическая, коэффициент вариации, коэффициент корреляции, критерии различия и другие точечные статистики должны получить количественные границы доверия, которые обозначают возможные колебания показателя в меньшую и большую стороны в пределах доверительного интервала.

Пример 3.1. Распределение кальция в сыворотке крови обезьян, как было установлено ранее, характеризуется следующими выборочными показателями: = 11,94 мг%;= 0,127 мг%;n = 100. Требуется определить доверительный интервал для генеральной средней () при доверительной вероятностиP = 0,95.

Генеральная средняя находится с определенной вероятностью в интервале:

, где – выборочная средняя арифметическая;t – критерий Стьюдента; – ошибка средней арифметической.

По таблице «Значения критерия Стьюдента» находим значение при доверительной вероятности 0,95 и числе степеней свободы k = 100-1 = 99. Оно равно 1,982. Вместе со значениями среднего арифметического и статистической ошибки подставляем его в формулу:

или 11,69 12,19

Таким образом, с вероятностью 95%, можно утверждать, что генеральная средняя данного нормального распределения находится между 11,69 и 12,19 мг%.

Пример 3.2. Определите границы 95%-ного доверительного интервала для генеральной дисперсии () распределения кальция в крови обезьян, если известно, что= 1,60, приn = 100.

Для решения задачи можно воспользоваться следующей формулой:

, где – статистическая ошибка дисперсии.

Находим ошибку выборочной дисперсии по формуле: . Она равна 0,11. Значениеt- критерия при доверительной вероятности 0,95 и числе степеней свободы k = 100–1 = 99 известно из предыдущего примера.

Воспользуемся формулой и получим:

или 1,38 1,82

Более точно доверительный интервал генеральной дисперсии можно построить с применением (хи-квадрат) - критерия Пирсона. Критические точки для этого критерия приводятся в специальной таблице. При использовании критериядля построения доверительного интервала применяют двусторонний уровень значимости. Для нижней границы уровень значимости рассчитывается по формуле, для верхней –. Например, для доверительного уровня= 0,99= 0,010,= 0,990. Соответственно по таблице распределения критических значений, при рассчитанных доверительных уровнях и числе степеней свободыk = 100 – 1= 99, найдем значения и. Получаемравно 135,80, аравно70,06.

Чтобы найти доверительные границы генеральной дисперсии с помощью воспользуемся формулами: для нижней границы, для верхней границы. Подставим данные задачи найденные значенияв формулы:= 1,17;= 2,26. Таким образом, при доверительной вероятностиP = 0,99 или 99% генеральная дисперсия будет лежать в интервале от 1,17 до 2,26 мг% включительно.

Пример 3.3. Среди 1000 семян пшеницы из поступившей на элеватор партии обнаружено 120 семян зараженных спорыньей. Необходимо определить вероятные границы генеральной доли зараженных семян в данной партии пшеницы.

Доверительные границы для генеральной доли при всех возможных ее значениях целесообразно определять по формуле:

,

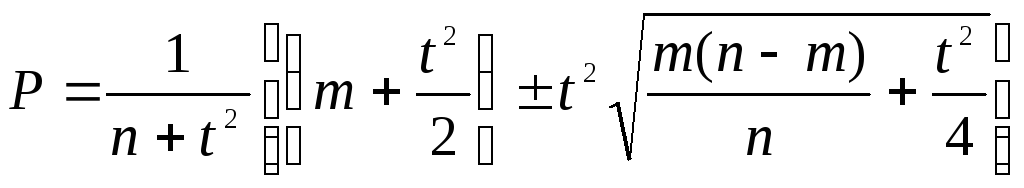Где n – число наблюдений; m – абсолютная численность одной из групп; t – нормированное отклонение.

Выборочная доля зараженных семян равна или 12%. При доверительной вероятностиР = 95% нормированное отклонение (t-критерий Стьюдента при k = )t = 1,960.

Подставляем имеющиеся данные в формулу:

0,122± 0,041

Отсюда границы доверительного интервала равны= 0,122–0,041 = 0,081, или 8,1%;= 0,122 + 0,041 = 0,163, или 16,3%.

Таким образом, с доверительной вероятностью 95% можно утверждать, что генеральная доля зараженных семян находится между 8,1 и 16,3%.

Пример 3.4. Коэффициент вариации, характеризующий варьирование кальция (мг%) в сыворотке крови обезьян, оказался равным 10,6%. Объем выборки n = 100. Необходимо определить границы 95%-ного доверительного интервала для генерального параметра Cv.

Границы доверительного интервала для генерального коэффициента вариации Cv определяются по следующим формулам:

и , гдеK промежуточная величина, вычисляемая по формуле .

Зная, что при доверительной вероятности Р = 95% нормированное отклонение (критерий Стьюдента при k = )t = 1,960, предварительно рассчитаем величину К:

.

или 9,3%

или 12,3%

Таким образом, генеральный коэффициент вариации с доверительной вероятностью 95% лежит в интервале от 9,3 до 12,3%. При повторных выборках коэффициент вариации не превысит 12,3% и не окажется ниже 9,3% в 95 случаях из 100.

Вопросы для самоконтроля:

1. Что такое вероятность?

2. Какие вероятности считаются доверительными?

3. Дайте определение терминов «доверительные границы» и «доверительный интервал».

4. Каков доверительный интервал при нормальном распределении с вероятностью 0,95; 0,99?

5. Что такое уровень значимости? Какая связь между уровнем значимости и вероятностью? Можно ли выражать уровень значимости в процентах?

6. На что указывает процентная величина уровня значимости?

7. В каких пределах по отношению к выборочной совокупности может находиться средняя арифметическая генеральной совокупности? С какой вероятностью?

8. Изменяются ли доверительные границы и доверительный интервал для μ при разных величинах n? Когда надо пользоваться t – распределением Стьюдента?

Задачи для самостоятельного решения.

1. Средний процент жира в молоке за лактацию коров холмогорских помесей был следующим: 3,4; 3,6; 3,2; 3,1; 2,9; 3,7; 3,2; 3,6; 4,0; 3,4; 4,1; 3,8; 3,4; 4,0; 3,3; 3,7; 3,5; 3,6; 3,4; 3,8. Установите доверительные интервалы для генеральной средней при доверительной вероятности 95% (20 баллов).

2. На 400 растениях гибридной ржи первые цветки появились в среднем на 70,5 день после посева. Среднее квадратическое отклонение было 6,9 дня. Определите ошибку средней и доверительные интервалы для генеральной средней и дисперсии при уровне значимости W = 0,05 и W = 0,01 (25 баллов).

3. При изучении длины листьев 502 экземпляров садовой земляники были получены следующие данные: = 7,86 см; σ = 1,32 см, =± 0,06 см. Определите доверительные интервалы для средней арифметической генеральной совокупности с уровнями значимости 0,01; 0,02; 0,05. (25 баллов).

4. При обследовании 150 взрослых мужчин средний рост был равен 167 см, а σ = 6 см. В каких пределах находится генеральная средняя и генеральная дисперсия с доверительной вероятностью 0,99 и 0,95? (25 баллов).

5. Распределение кальция в сыворотке крови обезьян характеризуется следующими выборочными показателями: = 11,94 мг%, σ = 1,27, n = 100. Постройте 95%-ный доверительный интервал для генеральной средней этого распределения. Рассчитайте коэффициент вариации (25 баллов).

6. Было изучено общее содержание азота в плазме крови крыс-альбиносов в возрасте 37 и 180 дней. Результаты выражены в граммах на 100 см³ плазмы. В возрасте 37 дней 9 крыс имели: 0,98; 0,83; 0,99; 0,86; 0,90; 0,81; 0,94; 0,92; 0,87. В возрасте 180 дней 8 крыс имели: 1,20; 1,18; 1,33; 1,21; 1,20; 1,07; 1,13; 1,12. Установите доверительные интервалы для разницы с доверительной вероятностью 0,95 (50 баллов).

7. Определите границы 95%-ного доверительного интервала для генеральной дисперсии распределения кальция (мг%) в сыворотке крови обезьян, если для этого распределения объем выборки n = 100, статистическая ошибка выборочной дисперсии s_σ2 = 1,60 (40 баллов).

8. Определите границы 95%-ного доверительного интервала для генеральной дисперсии распределения 40 колосков пшеницы по длине (σ² = 40, 87 мм²). (25 баллов).

9. Курение считают основным фактором, предрасполагающим к обструктивным заболеваниям легких. Пассивное курение таким фактором не считается. Ученые усомнились в безвредности пассивного курения и исследовали проходимость дыхательных путей у некурящих, пассивных и активных курильщиков. Для характеристики состояния дыхательных путей взяли один из показателей функции внешнего дыхания – максимальную объемную скорость середины выдоха. Уменьшение этого показателя – признак нарушения проходимости дыхательных путей. Данные обследования приведены в таблице.

Группа	Число обследованных	Максимальная объемная скорость середины выдоха, л/с
		Среднее	Стандартное отклонение
Некурящие
работают в помещении, где не курят	200	3,17	0, 74
работают в накуренном помещении	200	2,72	0, 71
Курящие
выкуривающие небольшое число сигарет	200	2, 63	0, 73
выкуривающие среднее число сигарет	200	2, 29	0, 70
выкуривающие большое число сигарет	200	2, 12	0, 72

По данным таблицы найдите 95% доверительные интервалы для генеральной средней и генеральной дисперсии для каждой из групп. В чем заключаются различия между группами? Результаты представьте графически (25 баллов).

10. Определите границы 95%-ного и 99%-ного доверительного интервала для генеральной дисперсии численности поросят в 64 опоросах, если статистическая ошибка выборочной дисперсии s_σ2 = 8, 25 (30 баллов).

11. Известно, что средняя масса кроликов составляет 2,1 кг. Определите границы 95%-ного и 99%-ного доверительного интервала для генеральной средней и дисперсии при n = 30, σ = 0,56 кг (25 баллов).

12. У 100 колосьев измеряли озерненность колоса (Х), длину колоса (Y) и массу зерна в колосе (Z). Найти доверительные интервалы для генеральной средней и дисперсии при P₁ = 0,95, P₂ = 0,99, P₃ = 0,999, если = 19, = 6,766 см, = 0,554 г; σ _x² = 29, 153, σ _y² = 2, 111, σ _z² = 0, 064. (25 баллов).

13. В отобранных случайным образом 100 колосьях озимой пшеницы подсчитывалось число колосков. Выборочная совокупность характеризовалась следующими показателями: = 15 колосков и σ = 2,28 шт. Определите, с какой точностью получен средний результат () и постройте доверительный интервал для генеральной средней и дисперсии при 95% и 99% уровнях значимости (30 баллов).

14. Число ребер на раковинах ископаемого моллюска Orthambonites calligramma:

32	34	31	31	30	26	26	26	31	26
26	26	26	26	25	19	20	20	22

Известно, что n = 19, σ = 4,25. Определите границы доверительного интервала для генеральной средней и генеральной дисперсии при уровне значимости W = 0,01 (25 баллов).

15. Для определения удоев молока на молочно-товарной ферме ежедневно определялась продуктивность 15 коров. По данным за год каждая корова давала в среднем в сутки следующее количество молока (л): 22; 19; 25; 20; 27; 17; 30; 21; 18; 24; 26; 23; 25; 20; 24. Постройте доверительные интервалы для генеральной дисперсии и средней арифметической. Можно ли ожидать, что среднегодовой удой на каждую корову составит 10000 литров? (50 баллов).

16. С целью определения урожая пшеницы в среднем по агрохозяйству были проведены укосы на пробных участках площадью 1, 3, 2, 5, 2, 6, 1, 3, 2, 11 и 2 га. Урожайность (ц/га) с участков составила 39,4; 38; 35,8; 40; 35; 42,7; 39,3; 41,6; 33; 42; 29 соответственно. Постройте доверительные интервалы для генеральных дисперсии и средней арифметической. Можно ли ожидать, что в среднем по агрохозяйству урожай составит 42 ц/га? (50 баллов).