6. Основы ДисперсионнОго анализА

Цель – познакомить студентов с особенностями дисперсионного однофакторного анализа и научить алгоритмам решения таких задач.

При решении задач, когда необходимо сравнить одновременно несколько выборок, объединяемых в единый статистический комплекс, целесообразно использовать дисперсионный анализ. Этот метод основан на разложении общей дисперсии статистического комплекса на составляющие ее компоненты, сравнивая которые, друг с другом посредством F-критерия можно определить, какую долю общей вариации учитываемого признака обуславливает действие на него как регулируемых, так и не регулируемых в опыте факторов.

Дисперсионный анализ позволяет:

1. Оценить силы и достоверность влияний факторов;

2. Оценить разности частных средних и частных долей;

3. Провести регрессионный анализ ряда частных средних и разработать прогноз развития признака при заданном комплексе условий;

4. Оценить гетерогенность родителей – степени разнообразия их наследственных способностей;

5. Оценить наследуемость признаков и определенных групп особей при передаче генетической информации из поколения в поколение;

6. Проанализировать комбинационные способности производителе, как основы планирования селекционной работы.

В дисперсионном анализе признаки, изменяющиеся под воздействием тех или иных причин, называются результативными. Причины, вызывающие изменение величины результативного признака, принято называть факторами. Факторы обозначают прописными начальными буквами латинского алфавита (А, B, C…), учитываемые признаки – конечными (X, Y, Z). На один и тот же признак действует много факторов, однако в опыте регулируются лишь некоторые из них: их называют регулируемыми или организованными факторами. Степени интенсивности фактора называются градациями фактора. Градации принято обозначать теми же буквами, что и факторы. Частные группы, подобранные для каждой градации фактора, называются градациями комплекса.

Если испытывают действие на признак одного регулируемого фактора, дисперсионный комплекс будет однофакторным, если одновременно исследуют действие на признак двух, трех или большего числа регулируемых факторов, комплекс называется двух-, трех- и многофакторным. Числовые значения (даты) результативного признака могут распределяться по градациям комплекса равномерно, пропорционально и неравномерно. Поэтому дисперсионные комплексы называют равномерными, пропорциональными и неравномерными.

Пример 6.1. При испытании новой минеральной подкормки на привес подсвинков организован однофакторный дисперсионный комплекс. Изучается несколько степеней действия фактора: пять увеличивающихся доз подкормки – нулевая (контроль), одинарная, двойная, тройная и учетверенная. Для каждой дозы в случайном порядке подобраны по нескольку подсвинков: для первой три, для второй четыре и далее пять, четыре, четыре. В результате получился дисперсионный комплекс, приведенный в таблице.

Градации фактора	0	1	2	3	4	q = 5
Даты,	2; 3; 1	4; 3; 6; 3	5; 6; 4; 6; 9	9; 7; 6; 6	3; 6; 5; 6
Объем градаций,	3	4	5	4	4	N = 20
Сумма дат	6	16	30	28	20	= 100
Частные средние	2	4	6	7	5

Это комплекс однофакторный, неравномерный. Объем комплекса N = 20, число градаций q = 5, повторности по градациям 3, 4, 5, 4, 4. – общая средняя по всему комплексу.

В однофакторном дисперсионном комплексе рассчитываются три дисперсии: факториальная, случайная и общая.

–факториальная (межгрупповая) девиата это сумма взвешенных квадратов центральных отклонений частных средних по градациям от общей средней по всему комплексу:

–случайная (внутригрупповая) девиата это сумма квадратов центральных отклонений каждой даты от своей частной средней: =

–общая девиата, сумма квадратов центральных отклонений дат от общей средней по всему комплексу: =

=

На основании трех девиат однофакторного комплекса можно засчитать показатель силы влияния фактора по следующей формуле:

или 60,5%

Ошибка показателя силы влияния находится по формуле:

Для расчета критерия оценки влияния (показателя достоверности влияния) регулируемого в опыте фактора на результативный признак необходимо найти соответствующие дисперсии:

–факториальная дисперсия равна факториальной девиате деленной на число степеней свободы (число градаций без одного q – 1).

–случайная дисперсия равна случайной девиате, деленной на число степеней свободы (объем комплекса без числа градаций n – q)

–общая дисперсия равна общей дисперсии, деленной на число степеней свободы (объем комплекса без единицы N – 1)

Показатель достоверности влияния определяется по преобразованному критерию Фишера по формуле:

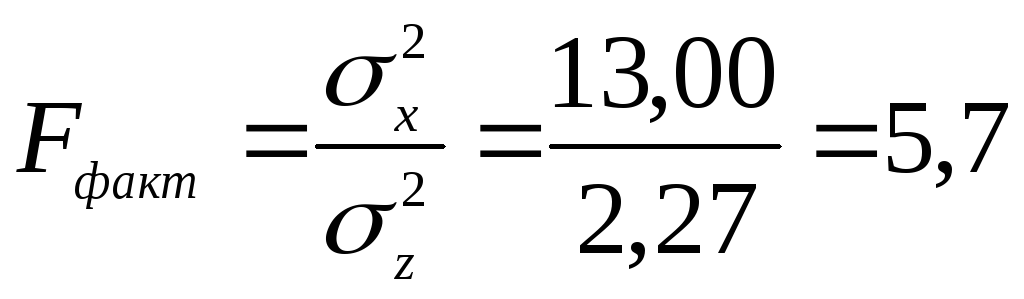
Стандартное значение критерия Фишера находим по таблице, пользуясь соответствующими степенями свободы: и

При доверительных вероятностях 95%, 99% и 99,9% равен 3,1; 4,9 и 8,3 соответственно. Сравнив величиныипри разных доверительных вероятностях установим, что фактический критерий Фишера больше стандартного при доверительной вероятности 99%, но меньше при доверительной вероятности 99,9%.

Таким образом, влияние минеральной подкормки на привес подсвинков за период наблюдения статистически достоверно при доверительной вероятности 99%.

После того, как достоверно установлено влияние регулируемого фактора на результативный признак, при необходимости прибегают к сравнению групповых средних друг с другом, как правило, контрольного (стандартного) и опытных вариантов.

Проведем сравнение контрольного варианта (градация 0) и опытного варианта (градация 3) групповые средние которых равны 2 и 7, соответственно. Для этого лучше использовать метод Шефе, который одинаково применим как к равно – так и неравновеликим по составу группам. Критерием достоверности различий, наблюдаемых между групповыми средними дисперсионного комплекса, служат следующие отношения:

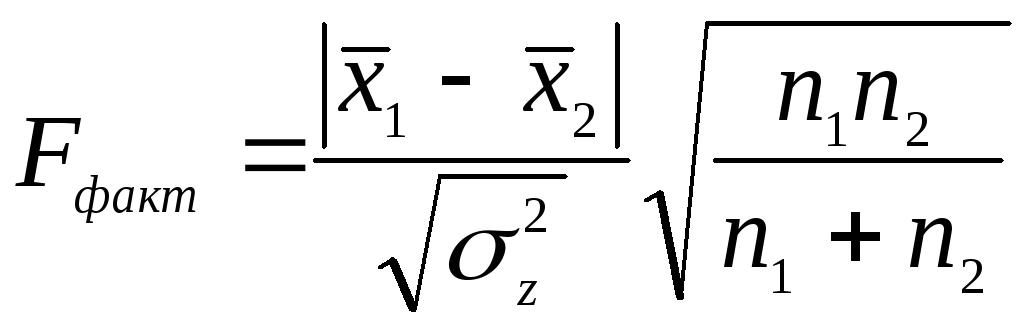(при );

(при );

Нулевая гипотеза отвергается, если

Для определения по таблице число степеней свободыи

Подставим в формулу имеющиеся значения

; иотсюда по таблице= 3,1 приP = 95%. Подставляем полученные значения в формулу и получаем 3,521. Так как, нулевая гипотеза остается в силе и разность между сравниваемыми вариантами опыта является статистически не доказанной. Очевидно, в дальнейшем необходимо увеличить объем выборочного комплекса.

Пример 6.2. Обычно, дисперсионный анализ дает возможность оценить силу и достоверность влияния факторов на какой-либо количественный признак, но может использовать и как показатель наследуемости. Чем выше показатель силы влиянии (), тем разнообразнее родители по своей способности давать лучшее или худшее потомство.

Посчитано количество щенков песца от разных самцов (А, В, С) у выровненного маточного поголовья самок. Данные приведены в таблице

Градации фактора	А	В	С	q = 3
Даты,	1;2;3	4;6	7;8;9
Объем градаций,	3	2	3	N = 8
Сумма дат	6	10	24	= 40
Частные средние	2	5	8

Отсюда = 54;=6;= 60, соответственно; ; .

Силу влияния фактора (в данном случае показатель наследуемости) определяем по формуле или 90%.

Показатель достоверности влияния определяем по критерию Фишера по формуле:

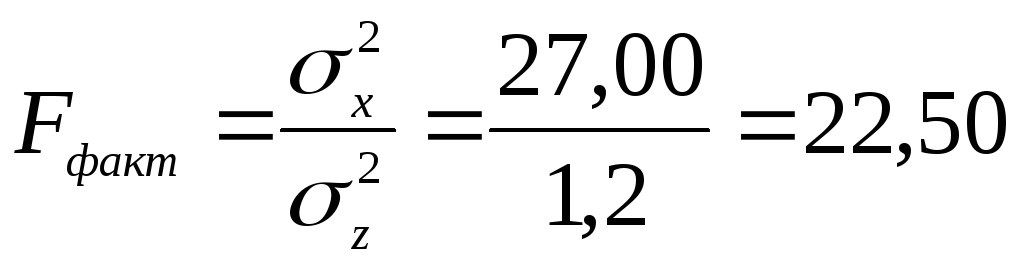
Стандартное значение критерия Фишера находим по таблице, пользуясь соответствующими степенями свободы: и

При доверительных вероятностях 95%, 99% и 99,9% равен 5,8; 13,3 и 36,6 соответственно. Сравнив величиныипри разных доверительных вероятностях установим, что фактический критерий Фишера больше стандартного при доверительной вероятности 99,9%.

Проведем сравнение плодовитости первого самца (градация А) и третьего (градация С) групповые средние которых равны 2 и 8, соответственно, по формуле: ;

Подставим в формулу имеющиеся значения

; иотсюда по таблице= 5,8 приP = 95%. Подставляем полученные значения в формулу и получаем 3,405. Так как, нулевая гипотеза отвергается, т.е. статистически доказано, что у самца С потомство более многочисленное, чем у самца А.

Таким образом, анализ, проведенный по этой схеме, показывает, что исследованная группа самцов в высшей степени неодинакова по своим наследственным способностям (количеству щенков в потомстве). Для получения наибольшего количества щенков целесообразно использовать в качестве производителя самца С.

Вопросы для самоконтроля.

1. В чем заключается сущность дисперсионного анализа?

2. Из каких компонентов складывается фактическое отклонение варианты от средней арифметической при одном контролируемом факторе?

3. Как установить достоверность влияния изучаемого фактора?

Задачи для самостоятельного решения.

1. На опытном участке агростанции изучали влияние различных способов внесения органических удобрений на урожай зеленой массы кукурузы. Опыт проводили на 10-метровых делянках в трех вариантах, не считая контроля. Каждый вариант опыта имел трехкратную повторность.

Результаты опыта приведены в таблице:

Варианты опыта	Урожай по повторностям, кг			Средний урожай
	1	2	3
Контроль	21,2	28,0	31,2	26,8
Удобрения помещали:
ниже семян на 4 см	23,6	22,6	28,0	24,7
в стороне от семян на 4 см	24,0	30,0	29,2	27,7
выше заделки семян на 4 см	29,2	28,0	27,0	28,1

Определите, достоверны или случайны различия между средними арифметических групп? (40 баллов).

2. Изучали продолжительность развития эмбрионов кроликов разных пород:

Породы	Продолжительность развития отдельных крольчат, день
Альбиносы	30	36	31	30	34	32	34	32	33	32
	35	32	31	33	33	35	31	33	32	33
Шиншилла	31	32	30	34	32	31	30	31	30	31
	30	32	31	32	30	31	33	32	32	33
Голландские	30	29	30	31	30	30	30	31	31	31
	30	31	29	32	31	31	30	31	31	31
Польские	30	31	29	30	29	30	29	31	29	30
	30	30	31	30	30	30	31	30	31	30

Влияет ли породность на продолжительность развития эмбрионов? (40 баллов).

3. У кубышки (Nuphar) четыре раза в сутки в десятикратной повторности определяли содержание каротиноидов:

Часы суток	Повторность
	1	2	3	4	5	6	7	8	9	10
18	1,42	1,30	1,68	1,59	1,49	1,62	1,36	1,26	1,58	1,66
24	1,45	1,38	1,49	1,71	1,54	1,57	1,34	1,32	1,66	1,39
6	1,48	1,42	1,58	1,67	1,50	1,80	1,35	1,36	1,67	1,49
12	1,43	1,38	1,47	1,33	1,22	1,35	1,10	1,08	1,34	1,11

Влияет ли время суток на содержание каротиноидов в листьях кубышки? (40 баллов).

4. У сирени (Syringa sp.) в разные часы суток в десятикратной повторности изучали содержание каротиноидов. Результаты были следующими:

Часы суток	Повторность
	1	2	3	4	5	6	7	8	9	10
18	0,60	0,64	0,69	0,52	0,65	0,52	0,58	0,63	0,69	0,48
24	0,61	0,72	0,72	0,58	0,46	0,52	0,72	0,59	0,71	0,79
6	0,58	0,59	0,66	0,46	0,47	0,56	0,70	0,60	0,60	0,64
12	0,70	0,57	0,67	0,87	0,52	0,66	–	0,59	0,65	0,66

Изменяется ли содержание каротиноидов в листьях сирени в течение суток? (40 баллов).

5. Получены следующие данные о содержании хлорофилла а (мг/дм²) в листьях канатника (Abutilon) в разное время суток:

Часы суток	Повторность
	1	2	3	4
15	3,06	2,88	2,83	2,41
18	3,20	2,97	2,50	3,03
21	1,82	1,73	1,33	2,25
24	1,67	1,26	1,52	1,36
6	2,76	1,26	1,46	1,32
9	2,78	2,70	2,49	1,66
12	2,41	3,22	1,90	2,00

Влияет ли время суток на содержание хлорофилла? (40 баллов).

6. Изучали живую массу ягнят-одинцов при рождении, ношенных разное число дней:

Длительность беременности	Живая масса ягнят, кг
145	3,8	2,9	3,3	3,6	3,8	3,7	4,8	5,1	3,4	3,3
146	3,7	2,9	3,3	3,6	3,9	3,7	4,7	5,0	3,4	3,2
147	3,9	4,1	4,4	5,0	3,0	2,9	4,0	3,2	4,2	4,3
148	4,0	5,2	4,3	2,9	4,1	3,9	3,2	3,9	4,1	4,0
149	4,0	5,3	4,2	3,0	4,0	3,9	4,2	3,3	4,0	4,1
150	4,1	4,3	5,4	3,1	4,0	4,0	4,3	3,9	4,0	4,1
151	4,3	4,2	5,5	4,2	4,1	4,1	4,4	3,5	4,1	3,6
152	4,3	3,6	4,4	5,5	4,0	4,1	4,5	4,1	4,2	4,3
153	4,4	4,7	3,9	4,6	5,7	4,3	4,8	4,9	4,7	4,7

Примените метод дисперсионного анализа для выяснения влияния длительность плодоношения на живой вес ягнят. (40 баллов).

7. Были получены следующие данные о содержании хлорофилла ав листьях томата (в услов. ед.) в различные часы суток:

Часы суток	Повторность
	1	2	3	4	5	6	7	8	9	10
18	0,22	0,27	0,22	0,23	0,20	0,28	0,32	0,28	0,29	0,27
24	0,23	0,24	0,24	0,26	0,23	0,25	0,26	0,28	0,30	0,23
6	0,25	–	0,19	0,24	0,20	–	0,30	0,27	0,20	0,26
12	0,24	0,28	0,25	0,27	0,22	0,27	0,32	0,30	0,29	0,27

Определите, оказывает ли влияние время суток на содержание хлорофилла а в листьях томата. (40 баллов).

8. Были получены следующие данные о содержании хлорофилла b в листьях томата (в услов. ед.) в различные часы суток:

Часы суток	Повторность
	1	2	3	4	5	6	7	8	9	10
18	0,087	0,106	0,091	0,097	0,077	0,103	0,118	0,104	0,099	0,108
24	0,086	0,092	0,095	0,100	0,086	0,096	0,101	0,113	0,113	0,092
6	0,093	–	0,091	0,089	0,081	–	0,118	0,106	0,088	0,096
12	0,088	0,091	0,104	0,113	0,079	0,097	0,114	0,107	0,103	0,093

Определите, оказывает ли влияние время суток на содержание хлорофилла b в листьях томата. (40 баллов).

9. На опытной рисовой станции проводились опыты по изучению влияния удобрений на урожай риса. В 1-й опытной группе применяли удобрение Р₂О₅+N; во 2-й – то же удобрение, а также предпосевную обработку почвы. Получены следующие данные:

Группы	Урожаи на делянках, ц/га
Контрольная	35	33	31	37	42	35	40
Опытная 1-я	43	48	54	–	–	–	–
Опытная 2-я	36	31	42	36	–	–	–

Проанализируйте полученные результаты. (45 баллов).

10. В опытах по изучению влияния синестрола в дозе 0,5 мг (инъекции масляного раствора и кристаллов) на вес яйцеводов пятисуточных цыплят получены следующие результаты:

Группы	Вес отдельных яйцеводов, мг
Масляной раствор	125	160	200	141	254	113
Кристаллы	23	40	130	122	44	120
Контроль	5	6	7	9	–	–

Примените метод дисперсионного анализа для установления влияния синестрола. Сравните средние арифметические отдельных групп, пользуясь величиной статистической ошибки по данным дисперсионного анализа. (50 баллов).

11. Получены следующие данные о плодовитости мышей при облучении рентгеновскими лучами:

Группы	Число мышат от отдельных самок
Контроль	10	12	11	10
Доза 100 р	8	10	7	9
Доза 200 р	7	9	6	4

Влияет ли облучение на плодовитость мышей? (40 баллов).

12. Годовые удои отдельных коров распределялись в зависимости от количества отелов следующим образом:

Количество отелов	Годовые удои отдельных коров, л
1	2115	2290	2230
2	2238	2364	2310
3	2462	2381	2236	2327
4	2381	2472	2415
5	2430	2375	2402	2405
6	2504	2471	2371	2400	2628
7	2439	2508	2439	2784

Можно ли утверждать, что количество отелов влияет на годовые удои коров? (45 баллов).

13. Изучали живая масса ягнят - одинцов при рождении (в кг), ношенных разное число дней:

Длительность беременности	Живая масса, кг
145	4,1	5,1	3,5	2,8	4,2	4,1	4,0	3,9	4,6	3,5
146	4,2	4,4	4,0	2,9	4,1	4,2	4,4	4,1	4,0	5,1
147	4,1	5,0	2,8	3,9	4,2	4,3	4,4	4,1	4,1	5,1
148	4,4	5,7	3,9	4,5	4,4	4,3	3,8	4,1	4,5	4,4
149	4,3	5,6	3,0	3,9	4,1	4,2	4,3	4,7	4,5	4,4
150	4,5	5,0	5,2	4,6	4,3	3,0	4,7	4,6	4,0	5,1
151	4,6	5,3	5,5	4,4	4,3	3,2	4,0

Установите, влияет ли длительность плодоношения на живой вес ягнят? (45 баллов).

14. Получены следующие данные о продолжительности эмбрионального развития коз при рождении их одинцами, двойнями, тройнями:

Группы по количеству козлят от одной самки	Длительность эмбрионального развития отдельных козлят, сут.
Одинцы	148	151	153	150	151	150	154	152	151	151	149	150	152
	152	151	150	152	149	148	151	152	152	152	151	151	150
Двойни	154	151	152	151	151	152	152	150	151	152	152	151	149
	152	148	150	151	151	153	152	149	151	148	149	150	151
Тройни	150	152	149	153	151	148	150	148	149	149
	147	148	150	149	152	149	148	149	149	148

Есть ли разница в продолжительности эмбрионального развития между козлятами - одинцами, двойнями и тройнями? Примените метод дисперсионного анализа и обычное сравнение средних арифметических (50 баллов).

15. Определяли концентрацию кальция в 3 листах на 4 растениях турнепса по 2 определения на каждый лист. Получены следующие данные (в % к сухому веществу):

Растение	Лист	Определения
1	1	3,28	3,09
	2	3,52	3,48
	3	2,88	2,80
2	1	2,46	2,44
	2	1,87	1,92
	3	2,19	2,19
3	1	2,77	2,66
	2	3,74	3,44
	3	2,55	2,55
4	1	3,78	3,87
	2	4,07	4,12
	3	3,31	3,31

Дайте оценку роли индивидуальности растений и различий между листьями по содержанию кальция. (40 баллов).

Литература

Глотов Н.В., Животовский Л.А., Хованов Н.В., Хромов-Борисов Н.Н. Биометрия. Л.: Изд-во Ленингр. ун-та, 1982. 264 с.

Гланц С. Медико-биологическая статистика. М.: Практика. 1998. 459 с.

Доспехов Б.А. Методика полевого опыта. М.: Агропроиздат, 1985. 351 с.

Зайцев Г.Н. Математическая статистика в экспериментальной ботанике. М.: Наука. 1984. 424 с.

Зайцев Г.Н. Методика биометрических расчетов. М.: Наука. 1973. 256 с.

Зайцев Г.Н. Оптимум и норма в интродукции растений. М.: Наука. 1983. 272 с.

Зайцев Г.Н. Фенология древесных растений. М.: Наука. 1981. 120 с.

Лакин Г.Ф. Биометрия. М: Высш. шк. 1990. 352 с.

Луценко А.И., Луценко Э.К., Ляхова Н.Ф. Введение в биометрию. Ростов н/Д.: Изд-во РГУ, 1986. 96 с.

Плохинский Н.А. Математические методы в биологии. М.: Изд-во МГУ. 1978. 265 с.

Рокицкий П.Ф. Биологическая статистика. Минск: Вышейш. школа. 1967. 328 с.

100