Лекции Физика / Лекция 13.б-1

1

Лекция № 13

Статистический и термодинамический методы.

Случайные величины и их описание. Физические основы молекулярнокинетической теории идеального газа. Уравнение состояния (уравнение Клапейрона-Менделеева). Равновесный квазистатический процесс.

Основное уравнение молекулярно-кинетической теории идеального газа.

Молекулярная физика и термодинамика - разделы физики, в которых изучаются тепловые процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода:

статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй – термодинамики.

Молекулярная физика – раздел физики, изучающий строение и свойства вещества, исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана еще Демокритом. Атомистика возрождается вновь лишь в XVIII веке и развивается в работах М.В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX века и связано с работами Клаузиуса, Максвелла и Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являются статистическими закономерностями. Такие законы поведения изучаются с помощью статистического метода.

Статистический метод основан на использовании теории вероятностей. В этом методе свойства макроскопической системы, в конечном счете, определяются свойствами частиц системы, особенностями их движения и усреднен-

ными значениями динамических характеристик этих частиц (скорости, энергии и т.д.). Так, если газ в объеме V содержит N молекул, движущихся со скоростями υ1,υ2 ,...,υ N , то целесообразно рассматривать среднюю квадратичную скорость:

Рассмотрим основные свойства вероятности. Теория вероятности изучает явления, которые имеют случайный характер. Случайным называется собы- тие, которое нельзя предсказать с определенностью. Этим оно отличается от достоверного события. Пример случайного события — приход определенной молекулы в заданную точку в результате беспорядочного теплового движения в газе частиц. Пример достоверного события — приход той же молекулы в заданную точку в результате движения по траектории с заданной скоростью без

2

столкновений. В первом случае появления “ меченой” молекулы в заданной точке можно ожидать с некоторой вероятностью.

Вероятностью P(A) некоторого события A называется частота появления данного события A в общем числе событий A. Ясно, что вероятность есть положительная величина. Из ее определения следует, что 0 ≤ P ≤ 1. Если событие достоверно, то P = 1. Если событие не может произойти вообще, то P = 0.

Вероятность сложного события, состоящего из двух независимых событий, равна произведению вероятностей каждого из независимых событий.

Случайное событие, в частности, может состоять в том, что какая-либо физическая величина имеет определенное, но произвольное значение. Такие ве- личины называются случайными. Случайные величины могут принимать как дискретные, так и непрерывные значения.

Если случайная физическая величина принимает непрерывный ряд значений x, то вероятность dP того, что величина x находится в бесконечно малом промежутке между x и x + dx, равна

Функция W(x) называется плотностью вероятности. Очевидно, ∫W (x)dx = 1.

Предположим, что случайная величина принимает ряд значений x1, x2,..., xN, с вероятностями P1, P2,..., РN. Тогда ее среднее значение (обозначается < x > или x ) определяется соотношением

Если x меняется непрерывно и плотность вероятности есть W(x), то среднее значение

Аналогично можно определить средние значения и других величин, например

среднего квадратичного значения случайной величины:

Однако всегда есть случайные отклонения от средних значений – флуктуации. Эти отклонения с равной вероятностью происходят в положительную и отрицательную сторону.

Далее, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение

3

скорости движения молекул. Нельзя говорить о температуре одной молекулы. Макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.

Термодинамика (ТД) – раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика – это теория тепловых явлений, в которой не учитывается молекулярное строение тел. В этой теории не вскрывается сущность тепловых процессов, и потому термоди-

намику называют феноменологической (описательной) теорией тепла.

Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. В термодинамике тепловые явления регистрируются приборами, не способными реагировать на воздействие отдельных молекул (термометр, манометр и др.).

Термодинамика имеет дело с термодинамической системой – совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией, как между собой, так и с другими телами (внешней средой). Основа тер- модинамического метода - определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами (макроскопическими параметрами состояния) – совокупностью физических величин, характеризующих свойства термодинамической системы: давление, объем, температура.

Термодинамика базируется на двух началах – фундаментальных законах (I и II законы ТД), установленных в результате обобщения опытных данных.

Область применения термодинамики значительно шире, чем молекуляр- но-кинетической теории (МКТ). Нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом.

С другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества.

МКТ и термодинамика взаимно дополняют друг друга, образуя единое целое, но различаясь различными методами исследования.

Из всего сказанного следует: несмотря на то, что каждая отдельная частица подчиняется законам механики, поведение системы большого числа частиц уже не может быть описано законами механики, а подчиняется законам статистической физики и термодинамики. Возникает вопрос: насколько большим должно быть число частиц в системе, чтобы ее описание с помощью законов механики становилось уже недостаточным, и система частиц проявляла бы макроскопические свойства. Для ответа на этот вопрос следует вспомнить, что говорить о существовании каких-либо физических свойств вещества можно только тогда, когда существует какой-либо способ их измерения. Иными словами, необходимо указать прибор, с помощью которого можно было бы произвести измерения соответствующих свойств. Процесс измерения представляет собой взаимодействие прибора с макроскопическим телом, и поэтому в процес-

4

се измерения все параметры системы изменяются на величину порядка энергии этого взаимодействия. Очевидно, что о макроскопических свойствах системы частиц можно говорить лишь в том случае, если взаимодействие мало изменяет состояние всей системы, так что средние значения всех физических величин в системе при измерении остаются практически неизменными. Если это требо-

вание выполняется, систему частиц можно считать большой. При этом точное значение числа частиц в системе не имеет никакого значения точно так же, как и характеристики отдельной частицы. Важно только, что это число частиц велико в указанном выше смысле. В реальных макроскопических телах числа частиц огромны — они составляют величину порядка 1020 частиц на 1 см3.

Основные положения МКТ, их опытное обоснование

иосновные понятия

1)Все вещества состоят из молекул или атомов.

Подтверждается химическими реакциями, прямыми микроскопическими наблюдениями (с помощью туннельного микроскопа), диффузией (проникновением молекул и атомов одних веществ в промежутки между молекулами и атомами других веществ), испарением вещества.

Молекула – это наименьшая частица данного вещества, сохраняющая химические свойства этого вещества.

Атом – это наименьшая частица химического элемента, обладающая его свойствами.

Размеры молекул и атомов определяются размерами орбиталей внешних электронов и составляют, примерно, 10 –10 м = 1 Å (ангстрем). При столь малых размерах молекул число их в любом макроскопическом теле велико. Так, мож-

но подсчитать, что в капле воды массой 1 г содержится N @ 3,7 ×1022 молекул.

Масса 1-ой молекулы воды равна: m0 @ 3×10− 23 г (очень малы массы молекул). Так как массы молекул очень малы, удобно использовать не абсолютные

значения масс, а относительные. По международному соглашению, принятому

в 1961 г., массы всех молекул сравнивают с 1 массы атома углерода (наиболее

12

распространенного изотопа углерода-12). Так называемая углеродная шкала атомных масс. Главная причина выбора углеродной шкалы атомных масс состоит в том, что углерод входит в огромное число различных органических соединений. Этот выбор позволяет очень точно сравнивать массы атомов тяже-

лых элементов с массой атома углерода. Множитель 1 введен для того, чтобы

12

относительные массы атомов были близки к целым числам.

Определение 1. Относительной молекулярной (или атомной) массой

Относительные атомные массы всех химических элементов точно измерены (и определяются из табл. Д.И. Менделеева). Складывая относительные атомные массы отдельных элементов, можно вычислить относительную молекулярную массу вещества, например, воды: M r (H2O) = 2 ×1 + 16 =18 ; медного купороса:

M r (CuSO4 ) = 64 + 32 + 16 × 4 =160 .

Принято сравнивать число молекул или атомов в данном теле с числом атомов, содержащихся в углероде массой 12 г. Относительное число атомов или молекул в теле характеризуется особой физической величиной, называемой количеством вещества.

[ν ]=1 моль — мера количества вещества в системе СИ.

{Моль — это количества вещества, содержащего в себе столько молекул, сколько атомов содержится в углероде массой 12 грамм.}

В 1 моле любого вещества содержится примерно 6 ×1023 молекул или атомов. Это было определено итальянским физиком Авогадро и называется числом

Авогадро: N A = 6,02 ×1023 моль-1.

Определение 3. Молярной массой М называют массу вещества, взятого в количестве одного моля:

где m0 - масса 1-ой молекулы.

Связь молярной массы (М) с относительной молекулярной массой ( M r ): M = M r ×10−3 кг/моль.

Число молекул N в теле рассчитывается по формуле:

2)Атомы и молекулы любых веществ находятся на определенном рас-

стоянии друг от друга. Причем численное значение этих расстояний зависит от агрегатного состояния данного вещества. Доказано, что расстояние между молекулами твердого вещества гораздо меньше, чем между молекулами газа.

То, что вещество может деформироваться свидетельствует о наличии расстояний между молекулами; это же можно показать и на примере диффузии.

3)Атомы и молекулы любых веществ находятся в непрерывном хаотиче- ском движении. Причем:

а) молекулы твердого вещества участвуют в колебательном движении (в узлах кристаллической решетки);

б) молекулы жидкости участвуют в колебательном и поступательном движении; {Время, в течение которого молекула жидкости колеблется, называется временем «оседлой» жизни.}

в) молекулы газа движутся поступательно.

Наряду с названными движениями молекулы твердого, жидкого и газообразного веществ участвуют в спиновом вращении (вращение вокруг собственной оси).

Подтверждается диффузией и броуновским движением — хаотическим движением микрочастиц под действием беспорядочных соударений молекул жидкости или газа.

{Английский ботаник Броун (1773-1858), наблюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что частицы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что подобное сложное зигзагообразное движение характерно для любых частиц малых размеров (около 1 мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды, с уменьшением вязкости и размеров частиц (независимо от их химической природы). Причина броуновского движения долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффекта ему было дано объяснение: броуновское движение взвешенных частиц вызывается ударами молекул среды, в которых частицы взвешены. Так как молекулы движутся хаотически, то броуновские частицы получают толчки с разных сторон, поэтому и совершают движение столь причудливой формы. Таким образом, броуновское движение является подтверждением выводов МКТ о хаотическом (тепловом) движении атомов и молекул.}

7

На рис.1 изображена траектория броуновской частицы.

4) Молекулы и атомы вещества взаимодействуют между собой с сила- ми, являющимися близкодействующими, так как эти силы действуют только то-

гда, когда расстояния между центрами молекул не превосходят, то есть меньше, двойного или тройного размера молекул данного вещества. У большей части веществ радиус молекулы лежит в пределах 10-8 — 10 -7 см.

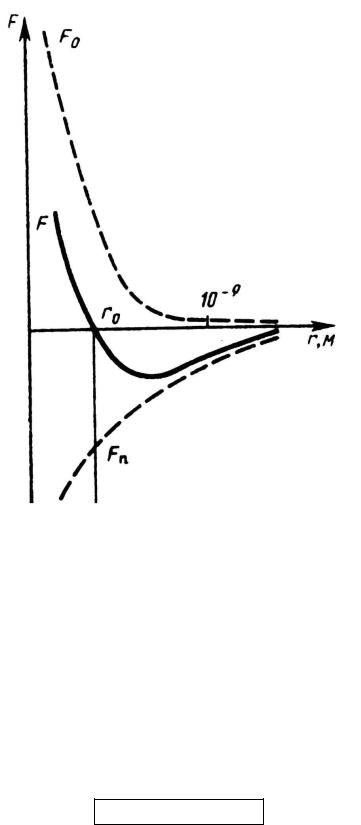
Характер сил взаимодействия (отталкивание или притяжение) определяется расстоянием между молекулами. В отсутствии внешних сил, действующих на вещество, это расстояние между молекулами строго определённо для каждого вещества и обозначается как r0 .

r0 - эффективный диаметр молекулы – это минимальное расстояние, на которое сближаются при столкновении центры двух молекул.

На рис.2 (сплошная линия) графически изображена зависимость проекции силы взаимодействия молекул от расстояния между их центрами.

Из графика зависимости силы взаимодействия между молекулами видим, что если обычное расстояние r0 уменьшать, то между молекулами начинают действовать силы отталкивания. Эта сила очень быстро увеличивается, когда электронные оболочки молекул начинают перекрываться.

Если же расстояние r0 увеличивать, то вступают в действие силы притяжения.

8

Рис.2

Итак, если r < r0 , то – отталкивание, Fr > 0 ;

если r = r0 , то Fr = 0 ;

если r > r0 , то – притяжение, Fr < 0 ;

если r >> r0 , то Fr ≈ 0 (силами взаимодействия можно пренебречь).

5) Любое вещество, в каком бы состоянии оно не находилось, обладает внутренней энергией, численно равной алгебраической сумме кинетической и потенциальной энергий и внутриатомной энергии ( E ):

U = Eкин + Eпот + E .

Данное положение подтверждается тем, что при нагревании вещества изменяется и кинетическая и потенциальная энергии молекул. А это ведет к превращению внутренней энергии в тепловую.

9

Термодинамические параметры. Идеальный газ. Уравнение состояния (уравнение КлапейронаМенделеева)

Любое макроскопическое тело (или группа макроскопических тел) назы-

вается термодинамической системой.

Термодинамическими (или макроскопическими) параметрами называют-

ся величины, характеризующие состояние термодинамической системы без учета молекулярного строения тел.

Обычно в качестве термодинамических параметров выбирают темпера-

туру (T), давление (p) и удельный объем ( v ) или объем (V).

Температура - одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.

В настоящее время применяют две температурные шкалы: Международная практическая шкал (шкала Цельсия), градуированная в

градусах Цельсия (° С) по двум реперным точкам — температурам замерзания и кипения воды при давлении 1,013·105 Па, которые принимаются соответственно 0° С и 100° С.

Термодинамическая температурная шкала определяется по одной репер- ной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,15 К. Температура T = 0 K называется нулем Кельвина. Градус Цельсия равен кельвину.

Термодинамическая температура (T) и температура (t) по Международной практической шкале связаны соотношением:

T = 273,15 + t .

Удельный объем - это объем единицы массы. Когда тело однородно, т.е. его плотность ρ = const , то v = V / m = 1/ ρ . Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства вещества однородного тела можно характеризовать объемом тела.

Тепловым или термодинамическим равновесием называют такое со-

стояние, при котором все макроскопические параметры сколь угодно долго остаются неизменными (при этом предполагается, что внешние условия рассматриваемой системы не изменяются). Это означает, что не меняется объем, давле-