Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский Государственный Технический Университет им. Ю.А. Гагарина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Физика / Лекция 09.б-1

.pdf

Скачиваний:

Добавлен:

12.02.2015

Размер:

262.56 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция № 9

Релятивистская механика.

Специальная теория относительности. Основные постулаты специальной теории относительности Эйнштейна. Преобразования Лоренца и следствия из них. Релятивистское выражение для импульса и энергии. Взаимосвязь массы и энергии.

Классическая механика Галилея-Ньютона прекрасно описывает движение макроскопических тел, движущихся с малыми скоростями. Однако в конце XIX века было установлено, что выводы классической механики противоречат некоторым опытным данным, в частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется известным законам механики.

Также возникли затруднения при попытках применить механику Ньютона к объяснению распространения электромагнитных волн и в частности, света. Если источник и приемник света движутся друг относительно друга, то, согласно классической механике, измеренная скорость света должна зависеть от относительной скорости движения источника и приемника. Майкельсон и Морли (1896г.) провели оптический эксперимент с использованием интерферометра по обнаружению движения Земли относительно эфира – гипотетической среды с особенными физическими свойствами, рассматриваемой в физике того времени в качестве абсолютной инерциальной системы отчета. Орбитальное движение Земли вокруг Солнца должно приводить к так называемому «эфирному ветру», оказывающему влияние на скорость распространения световых волн. Опыт показал отсутствие какого-либо влияния гипотетического «эфирного ветра» на скорость света. К аналогичным результатам привели и другие многочис-

ленные эксперименты, показывающие равенство значений скорости света в двух движущихся относительно друг друга системах отсчета.

Данный вывод противоречит фундаментальному правилу сложения скоростей механики Галилея-Ньютона.

Одновременно было выявлено противоречие между классической теорией и уравнениями Максвелла, лежащими в основе описания света как электромагнитной волны. Для объяснения этих и некоторых других опытных данных необходимо было создать новую механику, которая, объясняя эти факты, включала в себя ньютоновскую механику как предельный случай малых скоростей. Это удалось сделать А. Эйнштейну, который пришел к выводу, что мирового эфира - особой среды, которая могла бы быть принята в качестве абсолютной системы отсчета, не существует. Существование постоянной скорости распространения света в вакууме соответствует электродинамической теории Максвелла.

Специальная теория относительности Эйнштейна (СТО, релятиви-

сткая теория, 1905 г.) - современная физическая теория пространства и време-

ни, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно.

Основные постулаты СТО:

I. Принцип относительности.

Никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.

II. Принцип инвариантности скорости света.

Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

Первый постулат Эйнштейна является обобщением механического принципа относительности Галилея на любые физические процессы. Постулаты Эйнштейна и теория, построенная на их основе, привели к отказу от представлений об абсолютности пространства и времени и установили новые простран- ственно-временные представления, такие, например, как относительность длин и промежутков времени, относительность одновременности событий в различных системах отсчета, движущихся друг относительно друга.

Преобразования Лоренца

Рассмотрим две инерциальные				системы отсчета: К (с координатами
x, y, z ) и К' с координатами	′ ′	′	,	движущуюся относительно К (вдоль оси
	x , y , z

ОХ ) со скоростью υ = const (рис.1).

Рис.1

Пусть в начальный момент времени t = t′ = 0 , когда начала координат О и О' совпадают, излучается световой импульс в положительном направлении осей ОХ и ОХ’. В соответствии со вторым постулатом Эйнштейна, скорость света в обеих системах одинакова и равна c . Поэтому если за время t в системе К сигнал дойдет до некоторой точки А, пройдя расстояние x = ct , то в системе К' координата светового импульса в момент достижения точки А равна

x′ = ct′ , т.е.

x - x′ = c(t - t′) ¹ υ t .

Так как x ¹ x′ (система К' перемещается по отношению к системе К), то t ¹ t′ , т.е. отсчет времени в системах К и К' различен - отсчет времени имеет относительный характер (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т.е. t = t′ ).

Эйнштейн показал, что классические преобразования Галилея, описы-

вающие переход от одной инерциальной системы отсчета к другой:

K → K ′	K ′ → K
x'= x − υ t	x = x′ + υ t
		,
y'= y	y = y′	,

z'= z	z = z′

t'= t	t = t′

заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна.

Эти преобразования предложены Лоренцем в 1904г., еще до появления теории относительности, как преобразования, относительно которых уравнения Максвелла инвариантны.


K → K ′
		x − υ t
x'=

		1 − β 2
		1 − β 2

y'= y
z'= z

				υ x c		2
t'=	t −			υ x c


			1 − β		2
			1 − β

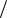где β = υc .

K ′ → K
	x′	+ υ t′
x =

	1 − β 2
	1 − β 2
		,	(9.1)
y = y′		,	(9.1)

z = z′

= t′ + υ x′ c2

1 − β 2

Из сравнения приведенных уравнений вытекает, что они симметричны и отличаются лишь знаком при υ . Это очевидно, так как если скорость движения системы К' относительно системы К равна υ , то скорость движения К относительно К' равна (− υ ).

Из преобразований Лоренца (9.1) вытекает также, что при малых скоростях (по

сравнению со скоростью c ), т.е. когда:

β = υ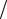c << 1,

они переходят в классические преобразования Галилея (принцип соответствия), которые являются предельным случаем преобразований Лоренца.

При β = υc > 1 выражения (9.1) для x, t, x′,t′ теряют физический смысл (становятся мнимыми). Это находится в соответствии с тем, что движение со скоростью, большей скорости распространения света в вакууме, невозможно.

Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе. Кроме того, как пространственные, так и временные преобразования не являются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени - пространственные координаты, т.е. устанавливается взаимосвязь пространства и времени.

Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматриваются неразрывно связанные пространственные и временные координаты, образующие че-

тырехмерное пространство-время.

Вводя обозначение γ =	1	,	преобразования Лоренца можно привести к

	1 - β 2

следующей симметричной форме:

x'			γ

y'			0
		=	0
	z'		0

			- βγ
t'			- βγ

- βγ

	x

	y
	×		(9.2)
	z

	t

Относительность одновременности как одно из следствий преобразований Лоренца

Пусть в системе К в точках с координатами x1 и x2 в моменты времени t1

и					′	и
и	t2 происходят два события. В системе К' им соответствуют координаты x1					и
x′	и моменты времени	t′	и	t′	. Если события в системе К происходят в одной
2		1		2

точке ( x1 = x2 ) и являются одновременными (t1 = t2 ), то согласно преобразова-

ниям Лоренца (9.1)	x′	= x′	и	t′	= t′	, т.е. эти события являются одновремен-
	1	2		1	2

ными и пространственно cовпадающими для любой инерциальной системы отсчета.

Если события в системе К пространственно разобщены ( x1 ¹ x2 ), но одновременны (t1 = t2 ), то в системе К', в соответствии с преобразованиями Лоренца:

x' =

1 − υ t

,x' =

2 − υ t

− β 2

/ c2 ,

(9.3)

t' =

t − υ x / c2

,t' =

t − υ x

1 − β 2

то есть x′	¹ x′	и t′ ¹ t′ , в системе К' эти события, оставаясь пространственно
1	2	1	2
разобщенными, оказываются и неодновременными.
		′	′	- x2 ), поэтому
Знак разности t1			- t2 определяется знаком выражения υ (x1	- x2 ), поэтому
				′	′
в различных точках системы отсчета К’ (при разных υ ) разность t1					- t2 будет

различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому.

Сказанное не относится к причинно-следственным событиям. Порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета. Чтобы причинно-следственная связь имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.

Для доказательства данного утверждения рассмотрим два события в покоящейся системе координат. Пусть событие в точке x1, происшедшее в момент

t1, является причиной события в точке x2 > x1 ,

происшедшего в момент t2 > t1 .

Скорость передачи «влияния» от точки x1 к точке x2 обозначим υin , тогда:

x2 − x1

= υin .

(9.4)

t2 − t1

′

В системе отсчета

в моменты вре-

К‘ эти события произошли в точках x1

мени t′

и t′

. В соответствии с преобразованиями Лоренца,

′

− t′ =

− t

− (υ c2 )(x

− x

)

− t )

1 −

(9.5)

1 − (υ c)2

			6
Для того, чтобы	′	′	(т.е. причина предшествовала следствию в системе от-
Для того, чтобы	t2	> t1	(т.е. причина предшествовала следствию в системе от-

счета К’, необходимо, чтобы υin < υc c . Так как преобразования Лоренца допус-

кают для υ значения, сколь угодно близкие, но не превышающие скорость света, то окончательно:

υin ≤ c

(9.6)

Т.е. передача физического влияния из одной точки в другую не может происходить со скоростью, превышающей скорость света. При этом условии причин-

но-следственная связь носит абсолютный характер: не существует систе-

мы координат, в которой причина и следствие меняются местами.

Хендрик Антон Лоренц (1853 - 1928)

Альберт Эйнштейн (1879-1955)

Выше была показана относительность понятия одновременности, следующая из преобразований Лоренца. Рассмотрим вопрос о длительности событий в различных системах отсчета.

Пусть в некоторой точке (с координатой x ), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний покоящихся часов в конце и начале события) τ 0 = t2 − t1 , где индексы 1 и 2 соответствуют началу и концу события, τ 0 - собственное время.

Длительность же этого события в системе К' :

		7
τ	′	′	′	,	(9.7)
τ		= t2	− t1	,	(9.7)

где в соответствии с преобразованиями Лоренца:

t' =	t −υ x / c2	, t' =	t	2	−υ x / c	2
	1			2			.	(9.8)
							.	(9.8)
1	1 − β 2	2			1 − β 2
	1 − β 2				1 − β 2

Подставляя (9.8) в (9.7), получаем:

τ '= t' -t' =					t	2 − t1			,
τ '= t' -t' =									,
2		1					- β 2
		1					- β 2
или:				τ 0
τ	'=			τ 0				(9.9)

			1 − β 2
			1 − β 2

т.е. τ 0 < τ ', или длительность события, происходящего в некоторой точке,

наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.

Этот результат может быть еще истолкован cследующим образом: интервал времени τ ' , отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала τ 0 , отсчитанного по его часам.

Следовательно, часы, движущиеся относительно ИСО, идут медленнее по-

коящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся. На основании относительности понятий "неподвижная" и "движущаяся" системы соотношения для τ ' и τ 0 обратимы. Из (9.9) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости распространения света в вакууме.

Релятивистский эффект замедления хода часов является совершенно реальным и получил экспериментальное подтверждение при изучении нестабильных, самопроизвольно распадающихся элементарных частиц в опытах с π- мезонами. Среднее время жизни покоящихся π-мезонов (по часам, движущимся вместе с ними) τ 0 » 2,2 ×10 −8 с. Следовательно, π-мезоны, образующиеся в верхних слоях атмосферы (на высоте порядка 30 км) и движущиеся со скоростью, близкой к скорости света, должны были бы проходить расстояния cτ 0 ≈ 6.6 м, т.е. не могли бы достигать земной поверхности, что противоречит действительности.

Объясняется это релятивистским эффектом замедления хода времени: для земного наблюдателя срок жизни π -мезона:

	8
τ '=		τ 0	,

	1 − β 2
	1 − β 2

а путь этих частиц в атмосфере:

υ ×τ '= c ×τ '=		c ×τ 0	.

	1 - β 2
	1 - β 2

Поскольку β ≈ 1, то υτ '>> cτ 0 .

Длина тела в различных системах отсчета

Рассмотрим стержень, расположенный вдоль оси x' и покоящийся относительно системы К'.

Длина стержня в системе К' будет l0' = x2' − x1', где x1' и x2' - не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится.

l0' = x2' − x1' - собственная длина стержня.

Определим длину этого стержня в системе К, относительно которой он движется со скоростью υ . Для этого необходимо измерить координаты его концов x1 и x2 в системе К в один и тот же момент времени t . Их разность и определяет длину стержня в системе К.

Используя преобразования Лоренца, получим:

= x' −x' =

2 −υ t

−

1 −υ t

x2 − x1

(9.10)

1 − β 2

То есть

или l = l' ×

1 - β 2 .

(9.11)

− β 2

Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя его длину в системе К', опять-таки придем к выражению (9.11).

Из выражения (9.11) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении дви-

жения в		1 - β 2		раз, т.е. так называемое лоренцево сокращение длины тем
больше, чем больше скорость движения.
	Из второго и третьего уравнений преобразований Лоренца следует, что
y' -y' = y		2	- y	и z' -z' = z		2	- z , т.е. поперечные размеры тела не зависят от
2	1		1	2	1		1

скорости его движения и одинаковы во всех инерциальных системах отсчета.

Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.

Релятивистский закон сложения скоростей

Рассмотрим движение материальной точки в системе К', в свою очередь движущейся относительно системы К со скоростью υ . Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами x, y, z , а в системе К' в момент времени t′ - координатами x', y', z' , то:


ux =		dx	,	uy =		dy	,	uz =	dz
										dt
		dt				dt
u'x =	dx', u'y =				dy',			u'z =		dz'.
	dt'				dt'					dt'

Полученные выражения представляют собой соответственно проекции на оси x, y, z и x', y', z' вектора скорости рассматриваемой точки относительно систем

Ки К'.

Всоответствии с преобразованиями Лоренца:

	dx'+υ dt'		dt'+υ dx'/ c2
dx =		, dy = dy', dz = dz', dt =

	1 - β 2		1 - β 2

Выполняя преобразования для dx , dy , dz , получим релятивистский закон dt dt dt

сложения скоростей:

K ′ → K

ux =

u'x +υ

υ × u'

/ c2

1 -

β 2

(9.12.1)

u y =

υ × u'

/ c2

uz =

1 - β 2

1 +υ × u'

/ c2

K → K ′

u'x

ux -υ

-υ × ux / c2

u'y =

u y

1 - β 2

(9.12.2)

-υ × ux / c2

u'z =

1 - β 2

-υ × ux / c2

Если материальная точка движется параллельно оси x , то скорость u от-

носительно системы К совпадает с ux ,

а скорость u′ относительно К' – с u′x .

Тогда закон сложения скоростей примет вид:

K ′ → K

K → K ′

u =

u'+υ

;

u'=

u -υ

(9.13)

1 + υ × u'/ c2

1 -υ × u / c2

Если скорости υ , u' и u малы по сравнению со скоростью света, то формулы (9.12) и (9.13) переходят в закон сложения скоростей в классической механике.

Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна. Действительно, если u'= c то формула (9.13) примет вид:

u = c + υ = c .

1 + υ × c / c2

Аналогично можно показать, что при u = c скорость u' также равна скорости света.

Полученный результат свидетельствует о том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна. Если складываемые скорости сколь угодно близки к скорости света, то их результирующая скорость всегда меньше или равна скорости света. Таким образом, при сложении любых скоростей результат не может превысить скорости света в ва-

кууме. Скорость света в вакууме есть предельная скорость, которую не-

возможно превысить. Скорость света в какой-либо среде, равная c / n , предельной величиной не является ( n - показатель преломления среды).

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции Физика

#
12.02.2015293.51 Кб43Лекция 04.б-1.pdf
#
12.02.2015225.78 Кб41Лекция 05.б-1.pdf
#
12.02.2015255.35 Кб41Лекция 06.б-1.pdf
#
12.02.2015280.31 Кб54Лекция 07.б-1.pdf
#
12.02.2015260.19 Кб49Лекция 08.б-1.pdf
#
12.02.2015262.56 Кб37Лекция 09.б-1.pdf
#
12.02.2015384.29 Кб39Лекция 10.б-1.pdf
#
12.02.2015315.22 Кб39Лекция 11.б-1.pdf
#
12.02.2015284.16 Кб42Лекция 12.б-1.pdf
#
12.02.2015393.08 Кб40Лекция 13.б-1.pdf
#
12.02.2015328.61 Кб40Лекция 14.б-1.pdf