
Лекции Физика / Лекция 04.б-1
.pdf
1
Лекция № 4
Законы сохранения в механике. Импульс материальной точки, системы материальных точек. Закон сохранения импульса. Центр масс системы материальных точек и закон его движения. Реактивное движение.
Энергия, работа, мощность. Работа силы. Кинетическая энергия материальной точки. Потенциальные силы. Потенциальная энергия системы взаимодействующих тел. Закон сохранения и изменения энергии в механике.
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, бу-
дут равны и противоположно направлены, т.е. геометрическая |
сумма внутрен- |
||
них сил равна нулю. |
|
|
|
Рассмотрим механическую систему, состоящую из n тел, массы и скоро- |
|||
сти которых соответственно равны |
m1, m2 , m3 ,....., mn и |
υ1,υ2 ,υ3 ,.....,υn ; |
|
F ' , F ' ,..., F ' - равнодействующие внутренних сил, действующие на каждое из |
|||
1 2 |
n |
|
|
этих тел; F1, F2 ,..., Fn - равнодействующие внешних сил. Второй закон Ньютона для каждого из тел системы:
d |
|
R |
R |
|
R |
|
|
|
|
|
|
|
|
(m υ |
) = F ' |
+F |
|
|
|
|
|
||
dt |
|
|
|
|
|
||||||
1 |
1 |
1 |
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
d |
|
R |
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
(m2υ2 ) = F '2 |
+F2 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
R |
R |
|
R |
|
|
|
|
|
|
|
(m3υ3 ) = F '3 +F3 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
dt |
|
|
|
|
|
d |
R |
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
||
× |
|
|
|
|
или |
|
(miυi ) = F |
'i +Fi . |
(4.1) |
||
|
|
|
|
dt |
|||||||
× |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
d ( R ) R R
mnυn = F 'n +Fn
dt
Почленное сложение этих уравнений дает:

2
d |
n |
R n |
R |
n |
R |
|
|
∑ |
(miυi ) = ∑ F 'i + ∑ Fi . |
(4.2) |
|||
|
||||||
dt i=1 |
i =1 |
|
i =1 |
|
|
|
Поскольку векторная сумма всех внутренних сил равна 0, то
d |
n |
R n |
R |
|
∑ |
(miυi ) = ∑ Fi . |
|
|
|||
dt i =1 |
i =1 |
|
|
С другой стороны, сумма импульсов всех тел, составляющих систему, равна импульсу системы:
R n R
p = ∑ pi
i =1
n |
R |
= ∑ |
(miυi ). |
i =1 |
|
Тогда
R |
R |
R |
R |
|
R |
n |
R |
|
|
|
dp |
|
dp |
|
|
||||||
= F1 |
+ F2 |
+ ... + Fn или |
|
= ∑ Fi |
. |
(4.3) |
||||
dt |
|
|||||||||
|
|
|
|
dt i=1 |
|
|
|
|||
Производная по времени от импульса механической системы равна векторной сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (замкнутая система):
|
|
|
|
|
|
|
|
|
R |
|
|
|
n |
|
|
|
dp |
|
|
R |
R |
|
|
|
|
= 0 |
, то есть |
p = ∑ miυi = const |
. |
||
|
dt |
||||||
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
Закон сохранения импульса
Импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.
В случае, когда сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление есть нуль, сохраняется составляющая импульса системы в этом направлении. Это следует из представления уравнения (4.3) в проекциях на оси декартовой системы координат:
dp |
x |
|
n |
|
||
|
|
|
= ∑ Fxi |
|
||
dt |
|
|||||
|
|
i =1 |
|
|||
|
|
|
|
|
n |
|
dp y |
|
= ∑ Fyi . |
(4.4) |
|||
|
|
|
|
|
||
dt |
|
|||||
|
|
i =1 |
|
|||
|
|
|
|
|
n |
|
dpz |
|
pz = ∑ Fzi |
|
|||
|
dt |
|
|
|
||
|
|
|
|
|
i=1 |
|

3
Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т.е. за-
кон сохранения импульса – фундаментальный закон природы. Закон сохране-
ния импульса является следствием определенного свойства пространства – его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала отсчета инерциальной системы.
Поскольку масса инвариантна, импульс системы может быть выражен через скорость ее центра масс.
Центром масс (или центром инерции) системы материальных точек назы-
вается воображаемая точка С, положение которой характеризует распределение массы этой системы.
Ее радиус-вектор равен:
|
|
|
|
|
n |
R |
|
|
|
|
|
|
|
|
∑ miri |
|
|
||
|
|
|
R |
= |
i=1 |
|
|
|
|
|
|
|
r |
|
|
, |
(4.5) |
||
|
|
|
|
||||||
|
|
|
C |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
- радиус-вектор, определяющий положение i -й материальной точки в |
|||||||
где |
ri |
||||||||
n
данной системе отсчета, m = ∑ mi - масса системы.
i =1
Дифференцируя (4.5) по времени, получим:
|
|
|
n |
R |
|
|
n |
|
|
|
|
|
|
dr |
|
|
R |
|
|||
|
R |
|
∑ mi |
i |
|
|
∑ miυi |
|
||
|
dt |
|
||||||||
R |
dr |
|
i=1 |
|
|
i =1 |
|
|
|
|
υC = |
C |
= |
|
|
= |
|
, |
(4.6) |
||
dt |
m |
|
|
|
|
|||||
|
|
|
|
|
|
m |
|
|||
где υC - скорость центра масс системы.
Учитывая, что |
R |
n |
R |
есть импульс системы, получим |
pi = miυi , а |
∑ pi |
|||
i=1
R = υ
p m C ,
т.е. импульс системы равен произведению массы системы на скорость ее центра масс.
Из определения радиус-вектора центра масс системы (4.5) видно, что если начало отсчета поместить в точку центра масс (Ц-система отсчета), то
4
n R
rC = 0 и, соответственно, ∑ miri = 0 .
i =1
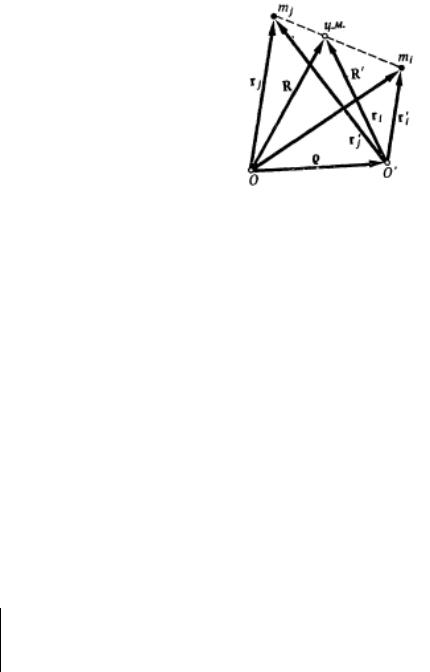
Вопрос: при смене начала отсчета, используемого для определения радиусвекторов точек системы, будет ли соответствовать центр масс в новой системе центру масс в исходной системе?
На рис.1 R - радиус-вектор центра масс системы относительно исходной системы отсчета О, R′ - радиус-вектор центра масс в системе отсчета О', ρ определяет положение О' относительно О.
|
|
|
|
|
Рис.1 |
|
|
|
|
|
∑ m r′ |
|
|
R |
R |
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
Тогда R′ = i i , учитывая, что ri′ = ri − ρ , получим: |
|
||||||||
|
m |
R′ |
|
|
|
|
|
|
|
|
R |
|
1 |
R |
R |
R |
R |
||
|
R′ = ∑ miri |
= |
∑ miri − |
1 |
ρ |
∑ mi = R − ρ . |
|||
|
m |
m |
|||||||
|
|
m |
|
|
|
|
|
||
Тем самым доказано, что положение центра масс в системе не зависит от того, в какой системе отсчета оно определяется.
Сопоставляя (4.3), (4.5) и (4.6), получим:
|
d |
R |
R |
R |
R |
|
|
m |
|
υ |
= F |
+ F |
+...+ F |
, |
(4.7) |
|
|||||||
|
dt |
C |
1 |
2 |
n |
||
|
|
|
|
|
|
|
т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная векторной сумме всех внешних сил, приложенных к системе. Выражение (4.7) пред-
ставляет собой закон движения центра масс.
Из закона сохранения импульса следует, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

5
Движение тел переменной массы
Движение некоторых тел сопровождается изменением их массы. Масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива. Получим уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени масса ракеты m , а ее скорость υ , то по истечении времени dt ее масса уменьшится на dm и станет равной (m − dm), а скорость станет равной (υ + dυ ).
Уравнение, описывающее изменение импульса системы за интервал времени dt , имеет вид:
R [ R R R R ] R
dp = (m − dm)(υ + dυ ) + dm(υ + u ) − mυ ,
где u - скорость истечения газов из ракеты. Тогда dp ≈ mdυ + udm . Если на ра-
кету действуют внешние силы, то |
R |
= Fdt . Окончательно получим уравнение |
|||||||||
dp |
|||||||||||
движения тела переменной массы или уравнение Мещерского: |
|
||||||||||
|
|
|
|
|
R |
|
R dm |
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dυ |
R |
|
|
|||
|
|
|
|
m |
|
= F |
− u |
|
|
|
(4.8) |
|
|
|
dt |
dt |
|||||||
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
ma = F + Fр , |
|
||||||
R |
R dm |
|
|
|
|
|
|
|
|
|
|
где Fр = −u |
|
- реактивная сила. |
|
|
|
|
|
|
|
||
dt |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Применим уравнение к движению ракеты, на которую не действуют никакие внешние силы. Полагая F = 0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим:
|
R |
R dm |
||
|
dυ |
|||
m |
|
= −u |
|
, |
dt |
|
|||
|
|
dt |
||
откуда
υ = −u∫ dmm = −u ln m + C .
Значение постоянной интегрирования определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m0 , то
C = u ×ln mo
и
m |
|
||
υ = u ×ln |
o |
|
- формула Циолковского. (4.9) |
|
|||
|
m |
|
|

6
Иван Всеволодович Мещерский
(1859—1935) — выдающийся рус-
ский учёный, ученик П.Л. Чебышева, основоположник механики тел переменной массы.
Константин Эдуардович Циолков-
ский (1857—1935)— российский и советский учёный-самоучка, исследователь, школьный учитель. Основоположник современной космонавтики.
Энергия – универсальная мера различных форм движения и взаимо-
действия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В
7
одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других – переходит в иную форму (например, в результате трения энергия механического движения переходит в тепловую). При этом существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, которые действуют на него со стороны других тел. Чтобы количественно характеризо-
вать процесс обмена энергией между взаимодействующими телами, в механи-
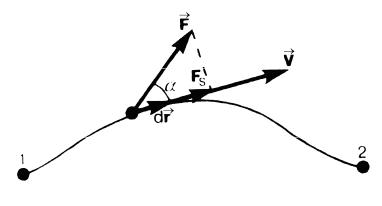
ке вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F , которая составляет некоторый угол α с направлением перемещения, то работа этой силы равна произведению проекции силы Fs = F cosα на перемещение точки приложения силы:
A = Fs s = Fs cosα . |
(4.10) |
В общем случае сила может изменяться как по модулю, так и по направлению.
Если рассматривать элементарное перемещение dr , то силу F |
можно считать |
||||||
постоянной, а движение точки ее приложения – прямолинейным. Элементар- |
|||||||
ной работой силы F на перемещении dr называется скалярная величина: |
|||||||
|
R |
, |
(4.11) |
||||
|
dA = F × dr = F cosα × ds = Fs × ds |
||||||
где α - угол между векторами F и dr , ds = |
|
R |
|
- элементарный путь, Fs - про- |
|||
|
|
||||||
|
dr |
|
|||||
екция вектора силы на направление dr (рис.2).
Рис.2
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых уча-
стках пути. Эта сумма сводится к интегралу:
2 |
2 |
|
A = ∫ Fds cosα = ∫ Fs ds . |
(4.12) |
|
1 |
1 |
|
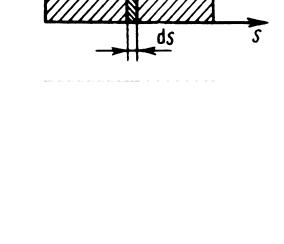
Для вычисления этого интеграла надо знать зависимость силы от пути вдоль траектории 1-2. Если такая зависимость представлена графически, тогда иско-
8
мая работа определяется на графике площадью заштрихованной фигуры
(рис.3).
Рис.3
В случае прямолинейного движения тела с F = const и α = const :
2 2
A = ∫ Fds cosα = F cosα ∫ ds = Fs cosα ,
1 1
где s - пройденный телом путь.
|
Как следует из определения работы, |
|
|
1) |
при α < π работа положительна, в этом случае составляющая F совпада- |
||
|
|
2 |
s |
ет по направлению с вектором скорости движения υ ; |
|
||
2) |
при α > π |
работа отрицательна; |
|
|
2 |
|
|
3) |
при α = π |
работа силы равна нулю, т.к. сила направлена перпендикулярно |
|
2
перемещению.
Единица измерения работы в системе СИ – джоуль. Работа в один джоуль соответствует работе силы в 1 Н при перемещении точки приложения силы на 1 м при α = 0 .
Чтобы охарактеризовать работу, совершаемую в единицу времени, вводят понятие мощности:
|
N = |
dA |
|
|
|
dt |
|
|
|
||
|
|
|
|
|
|
За время dt сила F совершает работу |
|
R |
, и мощность, |
||
F × dr |
|||||
силой, в данный момент времени: |
|
|
|
||
(4.13)
развиваемая этой
9
|
R |
|
|
|
|
|
F × dr |
R |
R |
|
|
N = |
= F |
×υ , |
(4.14) |
||
|
dt
т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
Единица мощности – ватт (Вт), соответствующий работе в 1 Дж, совершаемой за 1 с.
Кинетическая и потенциальная энергия
Кинетическая энергия механической системы – это энергия механиче-
ского движения этой системы.
Имеем покоящееся тело. На него действует сила F , под действием которой тело начинает двигаться. При этом сила совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до υ , идет на увеличение кинетической энергии, т.е.:
|
dA = dT . |
|
|
(4.15) |
||||
R |
|
R |
|
|
|
|
|
|
= m |
dυ |
|
|
|
|
|
|
|
Запишем 2-й закон Ньютона: F |
; |
|
|
|
|
|||
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= υdt , получаем: |
Умножим скалярно обе части на перемещение: dr |
||||||||
|
|
|
|
R |
|
|
|
|
R |
R |
dυ |
R |
|
||||
F |
× dr = m |
|
dr = dA |
, |
||||
|
||||||||
|
|
|
|
dt |
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
dA = mυdυ = mυdυ = dT |
||||||||
и далее: |
υ |
|
|
|
|
|
||
|
|
|
mυ 2 |
|
||||
T = ∫ mυdυ = |
|
. |
|
|||||
2 |
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тело массы m , двигающееся со скоростью υ , обладает кинетической энер-
гией:
T = |
mυ 2 |
. |
(4.16) |
|
2 |
|
|||
|
|
|
|
|
Кинетическая энергия зависит от массы и скорости тела, т.е. кинетическая энергия системы есть функция состояния ее движения. При выводе формулы
(4.16) предполагалось, что движение рассматривается в инерциальной системе отсчета (использовался второй закон Ньютона). В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кине-
тическая энергия зависит от выбора системы отсчета.

10
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Рассматриваются силовые поля, которые характеризуются тем, что рабо-
та, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Примеры таких полей - поля упругих и гравитационных сил. Такие поля называются по-
тенциальными, а силы, действующие в них, консервативными.
Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной
(например, сила трения).
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией U . Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
|
dA = −dU . |
(4.17) |
R |
, выражение (4.17) можно записать как: |
|
Поскольку dA = F × dr |
|
|
|
R |
(4.18) |
|
F × dr = -dU . |
Если известна функция U (r ), то из (4.18) можно найти силу F в различных точках как по модулю, так и по направлению.
Для консервативных сил:
|
|
|
|
|
|
|
|
|
|
|
|
F = - |
∂U , F |
y |
= - ∂U , F = - ∂U |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
¶x |
¶y |
|
z |
¶z |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или в векторной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
F = -gradU = - |
|
U |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ |
(4.19) |
|||||||||
где |
gradU = |
∂U R |
+ |
∂U |
R |
∂U |
R |
|
|
|
|
|
|
|
|
||||||||
¶x |
i |
¶y |
j + |
¶z |
k - градиент скалярной функции, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∂ R |
∂ |
R |
∂ |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ñ = |
|
i + |
|
|
j + |
|
|
k - оператор Гамильтона или набла-оператор. |
|||||||||||||||
|
¶y |
|
|
||||||||||||||||||||
|
|
|
¶x |
|
¶z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Потенциальная энергия может быть определена, исходя из (4.18), как |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
+ C |
, |
(4.20) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U = -∫ F × dr |
||||||||
где C - некоторая постоянная интегрирования.
Потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это не отражается на физических законах, так как в них
