Лекции Физика / Лекция 06.б-1

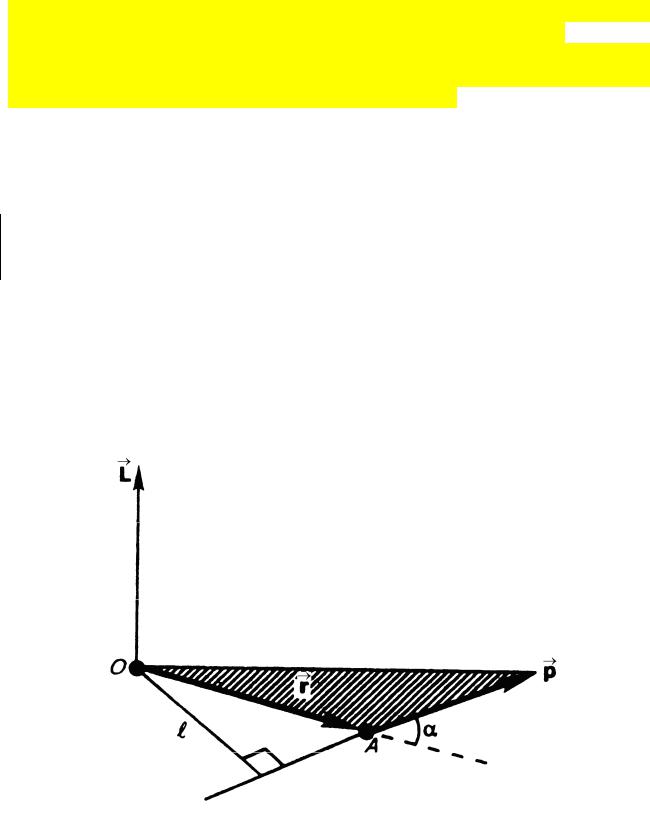
1

Лекция № 6

Динамика вращательного движения твердого тела относительно неподвижной оси.

Момент импульса материальной точки и системы материальных точек. Момент силы. Закон сохранения и изменения момента импульса. Кинетическая энергия твердого тела, совершающего поступательное и вращательное движения. Уравнение движения твердого тела, вращающегося вокруг неподвижной оси (уравнение моментов).

При сравнении законов вращательного и поступательного движений просматривается аналогия между ними: вместо силы рассматривается момент силы, роль массы играет момент инерции. Аналогом импульса тела является момент импульса тела относительно некоторой оси вращения.

Моментом импульса (количества движения) материальной точки А отно-

сительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

материальной точки (рис.1).

Вектор L - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p .

Рис.1

2

Модуль вектора момента: L = rp × sin α = rmυ × sin α = pl , где α - угол между векторами r и p ; l - плечо вектора p относительно точки О.

Моментом импульса относительно неподвижной оси z называется скаляр-

ная величина, равная проекции на эту ось вектора L момента импульса, определенного относительно произвольной точки О данной оси z . Момент импульса Lz не зависит от положения точки О на оси z .

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростьюυi (рис.2). Скорость υi и импульс miυi перпендикулярны

и направлен по оси в сторону, определяемую правилом правого винта.

Рис.2

Момент импульса твердого тела относительно оси есть сумма моментов им-

пульса отдельных частиц:

n

Lz = ∑ miυi ri . i =1

3

Используя соотношение υi = ωri , получим:

т.е. момент импульса твердого тела относительно неподвижной оси равен

произведению момента инерции относительно той же оси на угловую скорость.

Продифференцировав уравнение (6.3) по времени, получим:

– уравнение моментов - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная

момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

В общем случае имеет место векторное равенство:

Выражение (6.6) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения момента импульса – фундаментальный закон природы,

связанный со свойством симметрии пространства – его изотропностью, т.е.

с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).

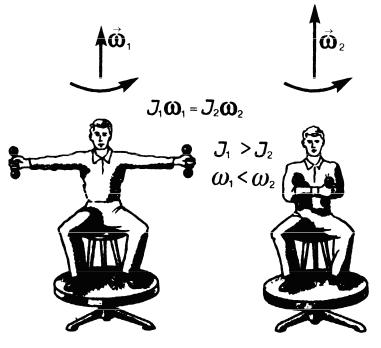
Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Человек, сидящий на скамье, которая без трения

4

вращается вокруг вертикальной оси, и держащий в вытянутых руках гантели, приводится во вращение с угловой скоростью ω1 (рис.3).

Рис.3

Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения возрастает.

Кинетическая энергия твердого тела, совершающего поступательное

ивращательное движения

Вслучае плоского движения тела, например, цилиндра, скатывающегося

снаклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

инерции тела относительно оси, проходящей через центр масс, ω - угловая скорость тела.

Условие отсутствия проскальзывания катящегося тела:

υC =υR = ω × R ,

5

где R - радиус катящегося тела. В частности, для сплошного цилиндра, катящегося без проскальзывания,

T = 3J C ×ω 2 . 2

Сопоставление основных физических величин и уравнений, определяющих вращение тела вокруг неподвижной оси и его поступательное движение