Лекции Физика / Лекция 05.б-1

1

Лекция № 5

Механика твердого тела. Момент инерции твердого тела относительно оси. Теорема Штейнера. Тензор инерции. Главные оси инерции.

Момент инерции твердых тел разной формы.

Момент инерции

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек, составляющих систему, на квадраты их расстояний до рассматриваемой оси:

i=1

Вслучае непрерывного распределения масс эта сумма сводится к интегралу:

где ρ - плотность вещества, из которого состоит тело, интегрирование проводится по всему объему тела, а величина r есть функция положения элементарного объема с координатами x, y, z внутри объема тела. При условии однород-

ности распределения плотности вещества по объему тела:

Если ρ - плотность материала, то масса элементарного цилиндра: dm = ρ × dV = ρ × 2πrhdr ,

а его момент инерции:

dJ = 2πρr 3hdr .

2

Тогда момент инерции сплошного цилиндра:

где m - масса цилиндра.

В таблице приведены значения моментов инерции некоторых однородных тел массой m .

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относи-

тельно произвольной оси равен моменту его инерции относительно параллельной оси, проходящей через его центр масс С, сложенному с произведением массы тела m на квадрат расстояния между осями a :

Проверка теоремы Штейнера для прямого тонкого стержня длиной l : 3-я строка таблицы:

J C = 1 ml 2 - ось вращения перпендикулярна стержню и проходит через его

12

середину.

Вычисляем момент инерции по теореме Штейнера, когда ось вращения перпендикулярна стержню и проходит через его конец ( a = l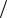2 ):

3

J = 1 ml 2 + 1 ml 2 = 1 ml 2

12 4 3 (сравнить со строкой 4 таблицы, где значение получено непосредственно интегрированием по длине стержня).

Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z , проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами m1, m2 ,..., mn , находящимися на расстояниях r1, r2 ,..., rn от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri и имеют различные линейные скорости ri (рис.2).

Рис.2

Поскольку рассматривается абсолютно твердое тело, то угловая скорость вра-

щения этих объемов одинакова:

ω = υ1 = υ2 = ... = υn . r1 r2 rn

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

T n miυi2 .

вр = ∑

i =1 2

4

Получим:

где J z - момент инерции тела относительно оси z . Таким образом, кинетиче-

ская энергия вращающегося тела:

Из сравнения формулы (5.6) с выражением для кинетической энергии тела, движущегося поступательно, следует, что момент инерции – мера инертности тела при вращательном движении. Формула (5.6) справедлива для тел, вра-

щающихся вокруг неподвижной оси.

Момент силы. Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси

Моментом силы F относительно неподвижной точки О называется физиче-

ская векторная величина, определяемая векторным произведением радиусвектора r , проведенного из точки О в точку А приложения силы, на силу F :

где r sinα = l - кратчайшее расстояние между линией действия силы и точкой О – плечо силы, α - угол между r и F .

Рис.3

5

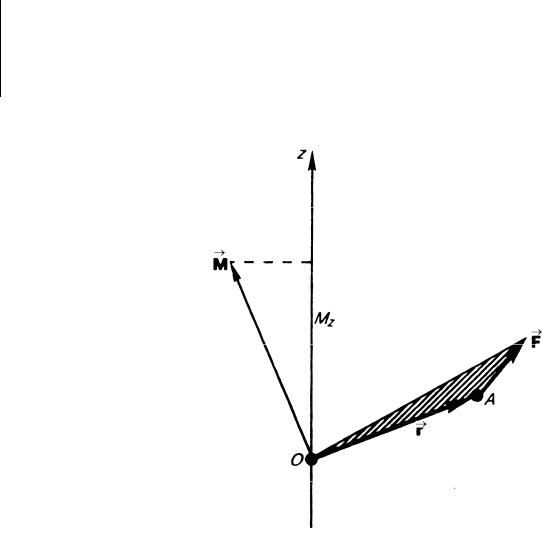
Моментом силы относительно неподвижной оси z называется скалярная ве-

личина M z , равная проекции на эту ось вектора M момента силы, определенного относительно произвольной точки О данной оси z (рис.4). Значение момента M z не зависит от выбора положения точки О на оси z .

Рис. 4

Если ось z совпадает с направлением вектора M , то момент силы представляется в виде вектора, совпадающего с осью:

= R .

M z [rF ]z

Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r . α - угол между направлением силы F и радиус-вектором r .

Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dϕ точка приложения силы (т.В) проходит путь ds = rdϕ (рис.5).

Работа равна произведению проекции силы на направление смещения на величину смещения:

6

z

dϕ

ds = r × dϕ

Рис.5

С учетом (5.8) последнее выражение можно записать: dA = M z dϕ ,

где F sinα × r = Fl = M z - момент силы относительно оси z . Таким образом, ра-

бота при вращении тела равна произведению момента действующей силы на угол поворота.

Работа при вращении тела идет на увеличение его кинетической энергии: dA = dT ,

- уравнение динамики вращательного движения твердого тела относи-

тельно неподвижной оси.

Если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство: