Лекции Физика / Лекция 03.б-1

1

Лекция № 3

Динамика. Взаимодействие материальных тел. Инерциальные и неинерциальные системы координат. Законы Ньютона. Масса. Сила. Уравнения движения.

Фундаментальные взаимодействия в природе. Силы в классической механике.

ИСО. Законы Ньютона

При рассмотрении кинематики использовалась неподвижная система отсчета. В природе не существует абсолютного движения, всякое движение имеет относительный характер: либо одного тела относительно другого, либо относительно выбранной системы отсчета. Возникает вопрос, все ли системы отсчета являются равноправными, а если нет, то какие являются предпочтительными. Единственное и естественное требование к системе отсчета состоит в том, что ее выбор не должен вносить усложнения в описание движения тел, т.е. законы движения в выбранной системе отсчета должны иметь наиболее простой вид. В частности, в такой системе должны оставаться неизменными свойства пространства и времени: пространство должно быть однородным и изотропным (это следует из евклидовой геометрии), а время - однородным.

Однородность пространства и времени означает, что наблюдаемые фи-

зические свойства и явления должны быть одинаковы в любой точке пространства и в любой момент времени. Не существует выделенных в каком-либо отношении точек пространства и моментов времени.

Изотропность пространства означает, что все направления в пространстве равнозначны. Физические явления в замкнутой системе не должны изменяться при ее повороте в пространстве.

Система отсчета, которая использовалась до сих пор, отвечала этим требованиям, но возникает вопрос, как ее реализовать, т.е. с какими объектами, реально существующими в природе, можно ее связать. Оказывается, что выбор подобной системы отсчета является непростым делом, так как требуемым условиям отвечает специальный класс физических объектов. Если «привязать» неподвижную систему координат к какому-либо произвольно движущемуся объекту, например к вагону поезда, можно заметить, что в данной системе отсчета сразу произойдут странные явления, например груз, подвешенный на нити, будет время от времени отклоняться от вертикали (что связано с действием различных ускорений вагона: при торможении или ускорении и при поворотах). В результате для описания этих явлений в данной системе координат придется прибегнуть к представлениям о взаимодействиях, внешних по отношению к системе, и включить их в рассмотрение. В то же время ясно, что в другой системе координат, не испытывающей указанных ускорений, описание механических явлений будет гораздо проще.

2

Другой пример не очень подходящей системы отсчета — неподвижная система, связанная с Землей. В этой системе можно, например, обнаружить вращение плоскости колебаний физического маятника (на самом деле связанное с вращением Земли вокруг своей оси), для объяснения которого нам также придется привлекать физические причины, являющиеся посторонними по отношению к данной системе отсчета. Вместе с тем, как показывает опыт, по отношению к Солнцу и звездам маятник будет вести себя стабильно, т.е. Солнце и звезды являются подходящими физическими объектами для выбора указанной системы отсчета.

Как показывает опыт, нужным требованиям удовлетворяют системы отсчета, которые связаны с физическими объектами, не испытывающими внешних воздействий, т.е. не подвергающимися каким-либо ус-

корениям. В таких системах отсчета тела находятся в состоянии покоя или равномерного прямолинейного движения до тех пор, пока на них не действуют другие тела. Свойст-

во тела сохранять такое состояние называется инерцией, и поэтому системы отсчета, о которых "идет речь", носят название инерциальных. Если наряду с выбранной инерциаль-

ной системой, рассмотреть другую, движущуюся относительно первой прямолинейно и равномерно, то свободное движение тела в новой системе будет также происходить с постоянной скоростью. Таким образом, существует бесконечное множество инерциальных систем отсчета. Во всех этих системах свой-

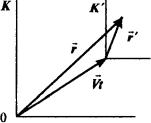
ства пространства и времени одинаковы и одинаковы законы механики. Не существует никакой абсолютной системы отсчета, которую можно было бы предпочесть другим системам. В этом состоит принцип относительности Галилея. Его можно сформулировать и так: никакими механическими опытами невозможно установить, движется ли данная инерциальная система или покоится: оба состояния эквивалентны. Координаты точки в двух системах отсчета, одна из которых K' движется равномерно и прямолинейно относительно другой (K) со скоростью V, связаны соотношением:

При этом считается, что время абсолютно, т.е. течет одинаково в обеих системах: t' = t. Скорость точки в системе К связана со скоростью в системе К' формулой:

Математически принцип относительности Галилея можно сформулировать как требование инвариантности (неизменности) уравнений механики по отношению к преобразованию (3.1)

3

Масса. Сила. Уравнение движения

Свойство, выражающее степень неподатливости тела к изменению его скорости, называется инертностью; количественной характеристикой инертности является масса тела. Введем понятие массы m , определив отношение масс двух различных тел по обратному отношению ускорений сообщаемых им равными силами:

В рамках ньютоновской механики масса обладает 2 важнейшими свойст-

вами:

1)является аддитивной величиной;

2)является постоянной величиной, не изменяющейся при движении.

Масса тела – физическая скалярная величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.

Доказано, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения).

В ньютоновской механике сила, действующая на тело массы m , определяется как произведение ma. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Сила является векторной величиной и в каждый момент времени характеризуется числовым значением, направлением в пространстве и точкой приложения.

Сила – это физическая векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Если рассмотреть действие различных сил на одно и то же тело, то ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующих приложенных сил:

Под действием одной и той же силы на тела с разными массами их ускорения различны:

Объединяя (3.4) и (3.5) с учетом векторного характера силы и ускорения, полу-

чим формулировку второго закона Ньютона:

Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В системе СИ: k = 1, поэтому второй закон Ньютона формулируется как:

гося тела. Более общая, по сравнению с (3.7), формулировка 2-го закона Ньютона имеет вид:

dt

Скорость изменения импульса материальной точки равна действующей на нее силе.

Выражения (3.7) и (3.8) – уравнения движения материальной точки.

Второй закон Ньютона справедлив только в инерциальных системах от-

счета. Первый закон Ньютона:

В инерциальной системе отсчета тело покоится ли движется равномерно и прямолинейно до тех пор, пока геометрическая сумма всех си, действующих на тело, равна нулю,

можно получить из второго. Действительно, в случае равенства нулю равно-

действующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в ко-

торых только и выполняются уравнения (3.7) и (3.8).

Принцип независимости действия сил: если на материальную точку дейст-

вует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было.

Пример применения принципа независимости действия: силы и ускорения можно разлагать на составляющие, использование которых приводит к сущест-

5

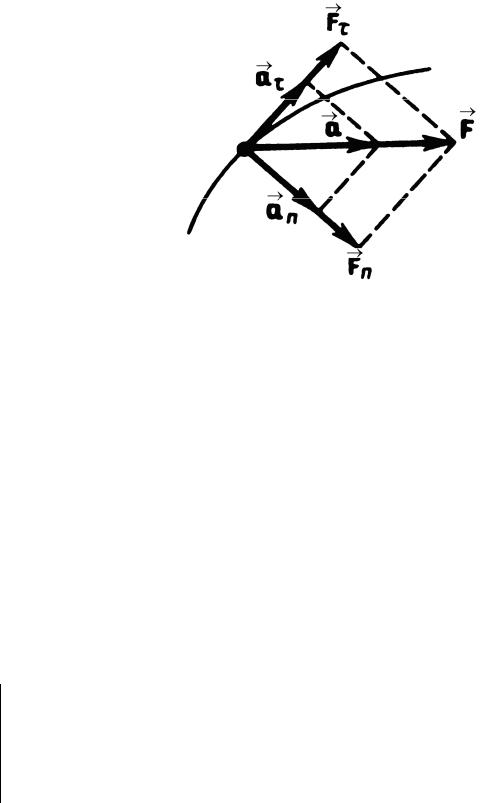
венному упрощению решения задач. При неравномерном движении тела по

на две составляющие: тангенциальную силу Fτ , направленную по касательной к траектории в рассматриваемой точке, и нормальную силу Fn , направленную по нормали к центру кривизны траектории в рассматриваемой точке.

Рис.1

Используя известные кинематические соотношения для тангенциального и нормального ускорений, можно записать:

где R - радиус кривизны траектории в рассматриваемой точке.

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под действующей силой во втором законе Ньютона понимают результирующую силу.

Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона:

всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F12 = −F21 .

6

Здесь F12 - сила, действующая на первую материальную точку со стороны вто-

рой, F21 - сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Третий закон Ньютона бывает справедлив не всегда. Он выполняется вполне строго в случае контактных взаимодействий, а также при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

В настоящее время в природе обнаружено четыре основных вида взаи-

модействия:

•электромагнитное,

•гравитационное,

•сильное и

•слабое.

Электромагнитное взаимодействие обусловливает взаимодействие ме-

жду заряженными частицами. Есть притяжение и отталкивание. Гравитационное взаимодействие, основным проявлением которого яв-

ляется закон всемирного тяготения, - всегда притяжение (гравитационное отталкивание не обнаружено). Притяжение между Землей и Солнцем заставляет Землю двигаться по круговой орбите вокруг Солнца. Сила тяжести - это та сила, которая заставляет загораться звезды. Она сообщает ядрам атомов необходимую для сближения кинетическую энергию (для преодоления силы электрического отталкивания), чтобы началась реакция термоядерного синтеза - основной источник энергии большинства звезд во Вселенной.

Сильное взаимодействие, в отличие от первых двух, является короткодействующим. Радиус его действия порядка 10-12 — 10 -13 см, то есть порядка размеров ядра атома. Это взаимодействие между нуклонами, протонами и нейтронами, и оно всегда имеет характер притяжения .

Слабое взаимодействие - взаимодействие, посредством которого реагирует с веществом такая неуловимая частица, как нейтрино. В полете сквозь космическое пространство, столкнувшись с Землей, она этого не замечает и прошивает ее насквозь. Примером процесса, в котором проявляется слабое взаимодействие, является так называемый β - распад нейтрона.

{В последнее время благодаря усилиям теоретиков удалось объединить электромагнитное и слабое взаимодействия в одно, что уменьшает число основных взаимодействий до трех.}

Сравнительная сила этих взаимодействий такова (см. табл. ниже): если интенсивность взаимодействия нуклонов (протонов и нейтронов) в ядре самая высокая, следующим по силе будет электромагнитное взаимодействие, затем слабое, и самым слабым является гравитационное взаимодействие.

7

Какие взаимодействия определяют все многообразие явлений на Земле? Гравитационное взаимодействие является очень слабым, однако оно обеспечивает то, что мы не улетаем с этой “ сцены” Земли в космическое пространство, то есть тяготение важно в том смысле, что оно удерживает на поверхности Земли воду, воздух и нас с вами. Ядерные силы на Земле проявляются не слишком сильно, иначе связанная с ними гигантская энергия уничтожила бы все живое.

Таким образом, основной движущей силой почти всех происходящих на Земле процессов являются электромагнитные силы и явления, ими вызываемые. Знание этих сил является основой для понимания химических реакций, биологических процессов, а значит и жизни, движения воздуха, воды и даже землетрясений.

Основные характеристики фундаментальных взаимодействий

Уровни энергий объединения взаимодействий: сильное или ядерное - 1015 ГэВ ; электромагнитное - 102 ГэВ ; слабое - 102 ГэВ; гравитационное - 1019 ГэВ.

Типичный современный уровень в исследованиях взаимодействия во встречных пучках - 103 ГэВ.

Большой адронный коллайдер (БАК, 2010) – 1.4 ×103 ГэВ.

Гравитационные силы. Движение в гравитационном поле

По второму закону Ньютона причиной изменения движения, то есть причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы опреде-

ляются действием сил тяготения. Закон всемирного тяготения был открыт И.

Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс. У тела в виде однородного шара центр масс совпадает с центром шара.

В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как дви-

8

жутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения: все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

F = G m1m2 . r2

Коэффициент пропорциональности G одинаков для всех тел в природе.

Его называют гравитационной постоянной G = 6,67·10–11 Н·м2/кг2 (СИ).

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна:

где g – ускорение свободного падения у поверхности Земли: g = G M .

R32

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли M:

2

= 5,98 ×1024 кг.

9

тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.

Космические скорости

Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость.

Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения долж-

на быть уравновешена центробежной силой mυ 2 , то есть

R3

mυ 2 = g M 3 ,

R3 R32

откуда находим значение первой космической скорости

Подставляя численные значения величин, получаем υI ≈ 8 км/с.

Вторая космическая скорость - это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:

A = Uк – Uн .

Потенциальная энергия тела в гравитационном поде Земли на ее поверхности имеет вид:

U = −G mM 3 ,

R3

а на бесконечности равна нулю.

Тогда

A = −G mM 3 = mgR3 . R3

Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу:

mυ 2 =

II mgR3 .

2

10

Отсюда вторая космическая скорость определяется выражением:

υII = 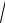2gR3 = 2 ×υI .

Ее численное значение υII ≈ 11 км/с.

Вес тела

Силу тяжести, с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни.

Весом тела P называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Вес приложен к опоре или подвесу (рис. 3).

Рис.3

Если опора покоится или движется равномерно и прямолинейно, то вес тела равен силе тяжести:

P = mg ,

но эти силы приложены к разным телам!

Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая силы пружины:

P = Fупр .

По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей.

Если опора движется с ускорением вверх (например, тело лежит на опоре или подвешено на пружине в кабине лифта, движущейся с некоторым ускорением относительно Земли), то вес увеличивается (+), вниз — уменьшается (-):

P = m(g ± а).

Если вектор ускорения направлен вертикально вверх, то a < 0 и, следовательно, вес тела всегда будет превышать по модулю силу тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают космонавты, как при взлете космической ракеты, так и на участке торможения при входе корабля в плотные слои атмосферы. Большие перегрузки испытывают летчики при выполнении фигур высшего пилотажа, особенно на сверхзвуковых самолетах.

При свободном падении (a = g) тело не давит на опору. Отсутствие веса (Р = 0) называется невесомостью. Такое состояние возникает, например, в ка-